Mở đầu trang 78 Toán 11 Tập 1: Để giải quyết vấn đề tắc đường ở các thành phố lớn, có rất nhiều giải pháp được đưa ra. Trong đó giải pháp xây dựng các hệ thống cầu vượt, đường hoặc đường sắt trên cao đã và đang được đưa vào thực tế ở Việt Nam. Toán học mô tả vị trí tương quan giữa các tuyến đường trên như thế nào?

Lời giải:
Toán học mô tả vị trí tương quan giữa các tuyến đường trên như những vị trí tương đối của đường thẳng trong không gian.
1. Vị trí tương đối của hai đường thẳng
HĐ1 trang 78 Toán 11 Tập 1: Hình 4.13 minh họa bốn tuyến đường (được coi là thẳng) tại một nút giao ở Hà Nội. Quan sát hình ảnh đó và trả lời các câu hỏi sau:
a) Hai tuyến đường nào giao nhau?
b) Hai tuyến đường nào không giao nhau?
c) Hai tuyến đường nào song song?

Lời giải:
Quan sát Hình 4.13 ta thấy:
a) Hai tuyến đường mũi tên màu đỏ và mũi tên màu vàng giao nhau.
b) Hai tuyến đường mũi tên màu xanh dương và màu xanh lá cây không giao nhau.
c) Hai tuyến đường mũi tên màu xanh dương và mũi tên màu đỏ song song.
Câu hỏi trang 79 Toán 11 Tập 1: Hãy tìm một số hình ảnh về hai đường thẳng song song, hai đường thẳng chéo nhau trong thực tiễn.

Lời giải:
+) Hình ảnh thực tế hai đường thẳng song song: hai cạnh đối diện chiếc bàn, các vạch kẻ đường, thanh lan can, …

+) Hình ảnh thực tế hai đường thẳng chéo nhau: cầu vượt và đường dưới, bóng đèn tuýp gắn trên tường và cạnh (không nằm trên tường treo đèn) của mặt tường bên cạnh,...

Luyện tập 1 trang 79 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành (H.4.17).
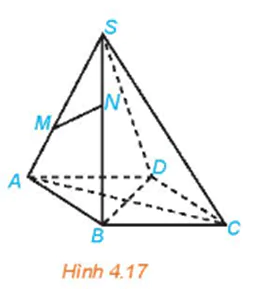
a) Trong các đường thẳng AB, AC, CD, hai đường thẳng nào song song, hai đường thẳng nào cắt nhau?
b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh SA, SB. Trong các đường thẳng SA, MN, AB có hai đường thẳng nào chéo nhau hay không?
Lời giải:
a) Hai đường thẳng AB và AC cắt nhau tại giao điểm A.
Hai đường thẳng AB và CD song song với nhau (do ABCD là hình bình hành).
Hai đường thẳng AC và CD cắt nhau tại giao điểm C.
b) Vì hai điểm M, N lần lượt là hai điểm thuộc hai cạnh SA, SB nên hai điểm M, N thuộc mặt phẳng (SAB) hay các điểm S, A, B, M, N cùng thuộc một mặt phẳng nên các đường thẳng SA, MN, AB đồng phẳng, do đó khi lấy bất kì 2 trong 3 đường thẳng trên thì chúng có thể cắt nhau hoặc song song hoặc trùng nhau. Vậy trong các đường thẳng SA, MN, AB, không có hai đường thẳng nào chéo nhau.
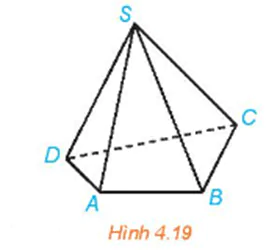
Luyện tập 2 trang 80 Toán 11 Tập 1: Trong hình chóp tứ giác S.ABCD (H.4.19), chỉ ra những đường thẳng:
a) Chéo với đường thẳng SA;
b) Chéo với đường thẳng BC.
Lời giải:
a) Các đường thẳng chéo với đường thẳng SA là BC và CD.
Giải thích: Nếu hai đường thẳng SA và BC không chéo nhau thì chúng cùng thuộc một mặt phẳng. Khi đó bốn điểm S, A, B, C đồng phẳng, trái với giả thiết S.ABCD là hình chóp. Do đó, hao đường thẳng SA và BC chéo nhau. Tương tự, giải thích được hai đường thẳng SA và CD chéo nhau.
b) Các đường thẳng chéo với đường thẳng BC là SA và SD. Giải thích tương tự câu a.
Vận dụng 1 trang 80 Toán 11 Tập 1: Một chiếc gậy được đặt một đầu dựa vào tường và đầu kia trên mặt sàn (H4.20). Hỏi có thể đặt chiếc gậy đó song song với một trong các mép tường hay không?

Lời giải:
Ta không thể đặt chiếc gậy đó song song với một trong các mép tường vì điểm đầu gậy chạm với sàn và 4 điểm góc của tường là các điểm không đồng phẳng nên đường thẳng tạo bởi chiếc gậy và một trong các mép tường là hai đường thẳng chéo nhau.
2. Tính chất của hai đường thẳng song song
HĐ2 trang 80 Toán 11 Tập 1: Trong không gian, cho một đường thẳng d và một điểm M không nằm trên d (H.4.21). Gọi (P) là mặt phẳng chứa M và d.
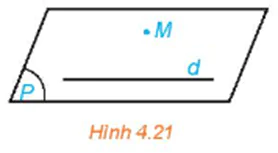
a) Trên mặt phẳng (P) có bao nhiêu đường thẳng đi qua M và song song với d?
b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) hay không?
Lời giải:
a) Trên mặt phẳng (P) có một và chỉ một đường thẳng đi qua M và song song với d (theo tiên đề Euclid).
b) Giả sử x là đường thẳng đi qua M và song song với d. Khi đó hai đường thẳng x và d đồng phẳng. Mà điểm M và đường thẳng d đều cùng nằm trong mặt phẳng (P) nên x và d cùng nằm trong mặt phẳng (P).
Vậy nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó thuộc mặt phẳng (P).
HĐ3 trang 80 Toán 11 Tập 1: Quan sát lớp học và tìm hai đường thẳng song song với mép trên của bảng. Hai đường thẳng đó có song song với nhau hay không?
Lời giải:
Hai đường thẳng song song với mép trên của bảng, ta có thể chọn là mép trên của tường có gắn bảng và mép dưới của bảng liền với tường, hai đường thẳng này có song song với nhau.
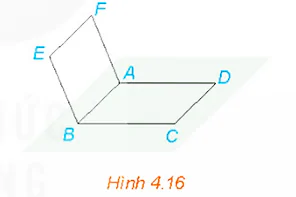
Luyện tập 3 trang 81 Toán 11 Tập 1: Trong Ví dụ 1, chứng minh rằng bốn điểm C, D, E, F đồng phẳng và tứ giác CDFE là hình bình hành.
Lời giải:
Ta có: EF // AB (do ABEF là hình bình hành) và CD // AB (do ABCD là hình bình hành).
Do đó, CD // EF.
Khi đó, hai đường thẳng CD và EF đồng phẳng hay bốn điểm C, D, E, F đồng phẳng.
Lại có EF = AB và CD = AB (do ABEF và ABCD là các hình bình hành) nên CD = EF.
Vậy tứ giác CDFE là hình bình hành.
HĐ4 trang 81 Toán 11 Tập 1: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến c. Một mặt phẳng (R) cắt (P) và (Q) lần lượt theo các giao tuyến a và b khác c.
a) Nếu hai đường thẳng a và c cắt nhau tại M thì đường thẳng b có đi qua M hay không (H.4.23)? Giải thích vì sao.
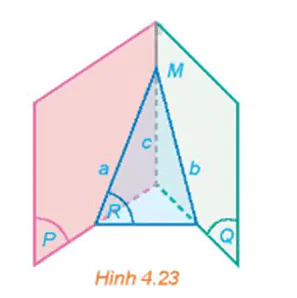
b) Nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c có song song với nhau hay không (H.4.24)? Giải thích vì sao.
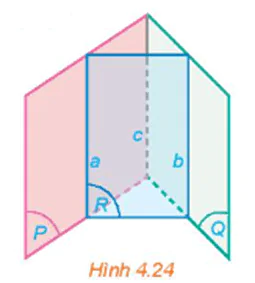
Lời giải:
a) Vì M thuộc a nằm trong mặt phẳng (R) nên M thuộc mặt phẳng (R).
Vì M thuộc c nằm trong mặt phẳng (Q) nên M thuộc mặt phẳng (Q).
Do đó, M là một điểm chung của hai mặt phẳng (R) và (Q).
Lại có hai mặt phẳng (R) và (Q) có giao tuyến là đường thẳng b.
Vậy M thuộc b hay đường thẳng b đi qua điểm M.
b) Ta thấy ba đường thẳng phân biệt a, b, c đôi một đồng phẳng.
Do đó, nếu không có hai trong ba đường thẳng nào trong chúng cắt nhau thì a, b, c đôi một song song.
Vậy nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c song song với nhau.
Luyện tập 4 trang 82 Toán 11 Tập 1: Trong Ví dụ 4, hãy xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).
Lời giải:
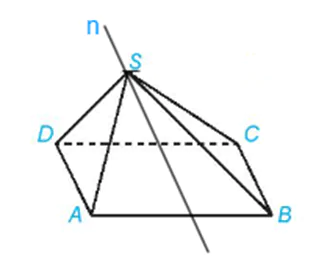
Hai mặt phẳng (SAD) và (SBC) có điểm chung S và chứa hai đường thẳng song song là AD và BC. Do đó, giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng n đi qua S và song song với AD, BC.
Vận dụng 2 trang 82 Toán 11 Tập 1: Một bể kính chứa nước có đáy là hình chữ nhật được đặt nghiêng như Hình 4.26. Giải thích tại sao đường mép nước AB song song với cạnh CD của bể nước.
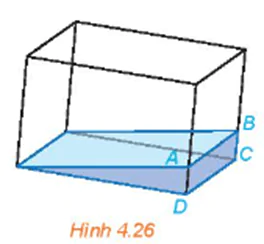
Lời giải:
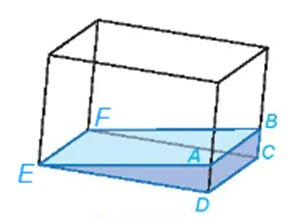
Giả sử mặt phẳng (ABFE) mà mặt nước, mặt phẳng (EFCD) là mặt đáy của bể kính và (ABCD) là một mặt bên của bể kính.
Ba mặt phẳng (ABFE), (EFCD) và (ABCD) là ba mặt phẳng đôi một cắt nhau theo các giao tuyến EF, AB và CD. Vì DC // EF (do đáy của bể là hình chữ nhật) nên ba đường thẳng EF, AB và CD đôi một song song. Vậy đường mép nước AB song song với cạnh CD của bể nước.











































































Bình Luận
Để Lại Bình Luận Của Bạn