(Trang 5)
| THUẬT NGỮ • Phép biến hình • Phép đồng nhất • Ảnh của một điểm • Ảnh của một hình | KIẾN THỨC, KĨ NĂNG • Nhận biết khái niệm phép biến hình. • Nhận biết khái niệm ảnh của một điểm, một hình qua một phép biến hình. |
Để biểu diễn sự phụ thuộc của một đại lượng vào một đại lượng khác ta đã đi đến khái niệm hàm số. Tương tự như vậy, trong bài học này ta sẽ xây dựng đối tượng cho phép biểu diễn sự phụ thuộc của một điểm vào một điểm khác.
1. PHÉP BIẾN HÌNH
>HĐ1. Hoa và Hưng cùng chơi trò sau: Hai bạn luân phiên nhau đặt các đồng xu có cùng kích thước lên trên một mặt mảnh giấy hình chữ nhật sao cho các xu nằm hoàn toàn trên mảnh giấy và xu đặt sau không chồng lên xu trước. Mỗi bạn, đến lượt mình được đặt một xu. Ai là người đầu tiên không còn chỗ để đặt xu là người thua cuộc.
(Trang 6)
| Sau vài lần chơi, Hoa đã phát hiện ra cách chơi để nếu được là người đặt xu trước, Hoa sẽ thắng cuộc. Hoa cho biết sẽ đặt đồng xu đầu tiên ở vị trí O ở chính giữa mảnh giấy và đưa ra quy tắc xác định vị trí đặt đồng xu kế tiếp mỗi đồng xu Hưng đặt. Hỏi nếu Hưng đặt đồng xu ở vị trí M thì đến lượt mình, Hoa sẽ đặt đồng xu ở vị trí nào? |  |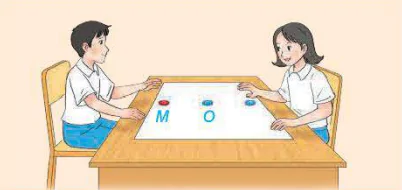
| Phép biến hình trong mặt phẳng là một quy tắc để ứng với mỗi điểm M thuộc mặt phẳng, xác định được duy nhất điểm M' thuộc mặt phẳng đó. Điểm M' được gọi là ảnh của điểm M qua phép biến hình đó. |
Chú ý
Nếu kí hiệu một phép biến hình là f và M' là ảnh của điểm M qua f, thì ta nói f biến điểm M thành điểm M'. Ảnh M' của M qua f được kí hiệu là f(M).
Phép biến hình biến mỗi điểm M thành chính M được gọi là phép đồng nhất.
| >Ví dụ 1. Trong mặt phẳng, cho đường thẳng d. a) Với mỗi điểm M, gọi M' là hình chiếu vuông góc của М lên d. Chứng minh rằng quy tắc cho tương ứng điểm M với điểm M' là một phép biến hình. b) Gọi a là một đường thẳng bất kì vuông góc với d. Chứng minh rằng tắt cả các điểm thuộc a có cùng ảnh qua phép n biến hình trên. |  |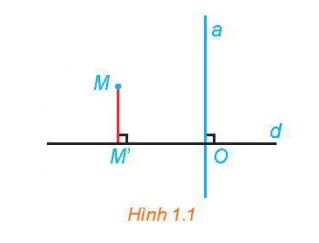
Giải
a) Mỗi điểm M đều có duy nhất hình chiếu vuông góc M' trên d (H.1.1). Do đó, quy tắc cho tương ứng điểm M với điềm M' như trên là một phép biến hình.
b) Gọi O là giao điểm của a và d. Khi đó, tất cả các điểm trên a đều có hình chiếu vuông góc trên d là O. Do đó, các điểm này có cùng ảnh là O qua phép biến hình nói trên.
2. ẢNH CỦA MỘT HÌNH QUA MỘT PHÉP BIẾN HÌNH
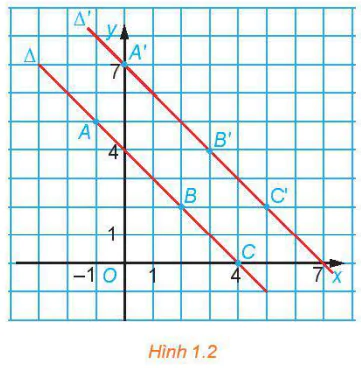
> HĐ2. Trên mặt phẳng toạ độ Oxy, cho phép biến hình f biến mỗi điểm M(x; y) thành điểm M'(x+1, y + 2).
a) Xét các điềm A(-1; 5), B(2, 2), C(4, 0) thuộc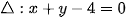 
Xác định các ảnh của chúng qua f.
b) Chứng minh rằng nếu M(x0; y0) là điểm thuộc đường thằng 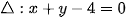thì ảnh M'(x0 + 1; y0 + 2) của nó thuộc đường thẳng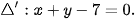 
(Trang 7)
Với mỗi hình  , ta gọi hình  gồm các điểm M'= f(M), trong đó M ∈ , là ảnh của hình qua phép biến hình f, và viết ). Khi đó, ta cũng nói f biến hình thành hình . |
>Ví dụ 2.Trên mặt phằng toạ độ Oxy, với mỗi số dương k khác 1 cho trước, xét phép biến hình f biến mỗi điểm M(x; y) thành điểm M'(x; ky).
a) Điểm N'(u0; v0) là ảnh qua f của điểm nào?
b) Chứng minh rằng, phép biến hình f biến đường tròn (C): x2 + y2 = R2 thành elip
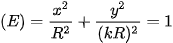
Giải
a) Điểm N'(u0; v0) là ảnh của điểm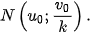 
b) Lấy điểm M(x0; y0) thuộc đường tròn (C), khi đó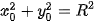 
và M có ảnh là M'(x0; ky0) Ta có
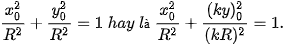Như vậy, M'(x0; ky0) thoả mãn phương trình elip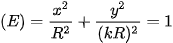
Vậy, nếu điểm M thuộc đường tròn (C) thì ảnh M'của nó thuộc elip (E).
Ta lại có, nếu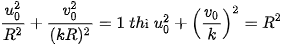 
Do đó, mỗi điểm N'(u0; v0) thuộc elip (E) đều là ảnh của điểm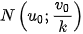 
Vậy f biến đường tròn (C) thành elip (E).
(Trang 8)
Chú ý
- Phép f trong Ví dụ 2 được gọi là phép co về trục hay dãn xa trục Ox nếu k tương ứng là nhỏ hơn hay lớn hơn 1.
- Các phép co, dãn biến đường tròn thành elip và biến elip thành elip hoặc đường tròn. Nhiều phần mềm về hình và xử lí hình ảnh có sử dụng phép co dãn. Chẳng hạn, trên một số phần mềm, để vẽ đường tròn, ta lại bắt đầu với một elip và sau đó điều chỉnh để hình chữ nhật cơ sở trở thành hình vuông (giữ nguyên một chiều của hình chữ nhật, chỉ điều chỉnh chiều còn lại).
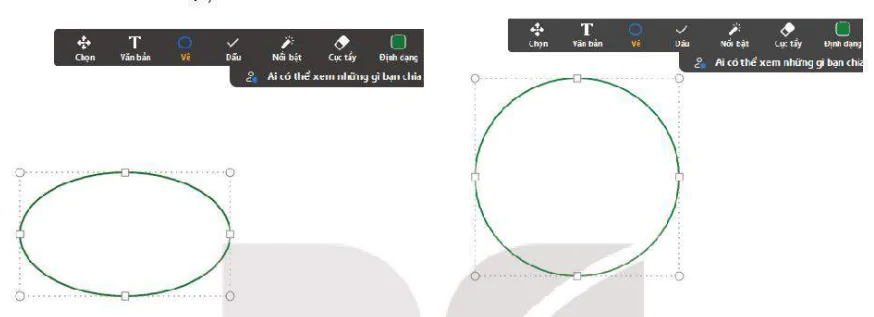
Hình 1.3: Vẽ đường tròn trên Witeboard bång cách bắt đầu với elip
>Vận dụng 1. Quan sát ba tấm ảnh hoa hồng ở Hình 1.4, hãy cho biết hình nào giống hình của hình ở giữa qua một phép co về trục.
Hình 1.4
BÀI TẬP
1.1. Trong mặt phẳng toạ độ Oxy cho điểm I(1; 2). Xét phép biến hình f biến điểm I thành điểm I và biến mỗi điểm M khác I thành điểm M' sao cho I là trung điểm của MM'. Tìm toạ độ ảnh của điểm A(3; - 2) qua phép biến hình f.
1.2. Trong bảng bên quan sát quy luật điền các cặp (A, A'), (B, B'), (C, C')...., từ đó điền các kí hiệu N', P', Q', R', S' vào các vị trí thích hợp.
| P | L' | N | M' | |
| R | K | S | I' | E' |
| B | H | G | A' | C |
| F' | D | D' | F | |
| C' | A | G' | H' | |
| E | I | K' | B' | |
| M | L | Q |
Các Bài Học Khác
Chuyên đề học tập Toán 11 - Bài 2: Phép Tịnh Tiến - Khái niệm và cách xác định phép tịnh tiến, hiểu về sự dịch chuyển đồng thời của mọi điểm trong mặt phẳng.
Xem thêm ⟶
Chuyên đề học tập Toán 11 - Bài 3: Phép Đối Xứng Trục - Cung cấp kiến thức về tính chất và cách thức biến đổi hình qua trục đối xứng.
Xem thêm ⟶
Bình Luận
Để Lại Bình Luận Của Bạn