(Trang 46)
| THUẬT NGỮ
| KIẾN THỨC, KĨ NĂNG
|
Trong bài học này chúng ta sẽ sử dụng kiến thức về đồ thị để giải quyết một số tình huống liên quan đến thực tiễn như bài toán tìm đường đi thoả mãn điều kiện cho trước (ngắn nhất, nhanh nhất, chi phí rẻ nhất, ...) trong một vài trường hợp đơn giản.
1. BÀI TOÁN TÌM ĐƯỜNG ĐI NGẮN NHẤT
| >HĐ. Cho sơ đồ như trên Hình 2.28, ở đó A, B, C, D, E, F là các địa điểm nối với nhau bởi các con đường với độ dài của mỗi con đường được cho như trên hình. a) Hãy chỉ ra 2 đường đi từ A đến F và so sánh độ dài của hai đường đi đó. b) Với mỗi đỉnh V của sơ đồ trên Hình 2.28, ta gán số l(V) là khoảng cách ngắn nhất để đi từ A đến V và gọi là nhãn vĩnh viễn của đỉnh V. Như vậy, ta có ngay l(A) = 0. Dựa vào Hình 2.28, hãy tìm các nhãn vĩnh viễn l(B), l(C) của hai đỉnh kề với A là B, C. | 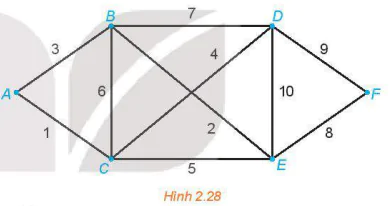 |
Để giải quyết bài toán tìm đường đi ngắn nhất nối A với F, chúng ta sẽ xem sơ đồ đó là đồ thị liên thông và mọi cạnh được gán với một số không âm, số đó chính là độ dài của đường. Những đồ thị như vậy gọi là đồ thị có trọng số và con số được gán với một cạnh gọi là trọng số của cạnh đó. Bài toán đặt ra là tìm đường đi từ A đến F với tổng các trọng số nhỏ nhất, tức là cần xác định nhãn vĩnh viễn I(F).
|
>Ví dụ 1. Tìm độ dài của đường đi ngắn nhất nối A với F trong đồ thị có trọng số trên Hình 2.28
Giải
Ta áp dụng thuật toán đã mô tả ở trên.
(Trang 47)
Đầu tiên ta gắn nhãn đỉnh A là l(A) = 0 và gán cho 2 đỉnh kề với A là B, C các nhãn tạm thời l(A) + 3 = 3, l(A) + 1 = 1. Chọn số nhỏ nhất trong chúng và viết l(C) = 1. Đỉnh C bây giờ được gán nhãn vĩnh viễn là 1.
Tiếp theo ta gắn cho các đỉnh kề với C là B, D, E các nhãn tạm thời l(C) + 6 = 7, l(C) + 4 = 5, l(C) + 5 = 6 (B hiện nay có hai nhãn tạm thời là 3 và 7). Nhận tạm thời nhỏ nhất trong các nhãn đã gán (ở B, D, E) hiện nay là 3 (tại B), nên ta viết l(B) = 3. Đỉnh B được gắn nhãn vĩnh viễn là 3.
Bây giờ ta xét các đỉnh kề với B (mà chưa được gán nhãn vĩnh viễn) là D và E. Ta gán cho đỉnh D hiện nay có hai nhãn tạm thời là 5 và 10), gán cho đỉnh E nhãn tạm thời l(B) + 2 = 5 (E có hai nhãn tạm thời là 6 và 5). Nhận tạm thời nhỏ nhất bây giờ là 5 (tại D và E), do đó ta viết l(D) = 5 và l(E) = 5. Hai đỉnh D và E đều được gắn nhãn vĩnh viễn là 5.
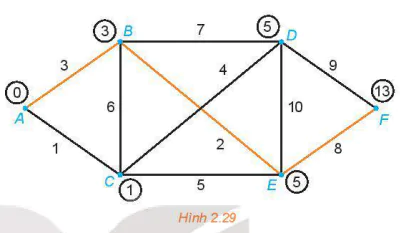
Xét đỉnh kề với D là F, ta gán cho F nhãn tạm thời l(D) + 9 = 14. Xét đỉnh kề với E là F, ta gán cho F nhãn tạm thời l(E) + 8 = 13. Vậy đỉnh F được gán nhãn vĩnh viễn là 13.
Vì l(F) = 13 nên đường đi ngắn nhất từ A đến F có độ dài là 13.
Để tìm một đường đi ngắn nhất từ A đến F như vậy, ta sẽ lần ngược từ điểm cuối F. Ta chỉ cần ghi hạn ở việc xét những cạnh mà độ dài là hiệu của các nhãn gắn tại các đầu mút của nó, đó là EF, BE và AB (do l(F) – l(E) = 13 – 5 = 8, l(E) – l(B) = 5 – 3 = 2 và l(B) – l(A) = 3 – 0 = 3). Khi đó ta có thể kết luận, đường đi ngắn nhất từ A đến F phải đi qua các cạnh EF, BE và AB.
Vậy, đường đi ngắn nhất (trong trường hợp này là duy nhất) từ A đến F là
A → B → E → F
Chú ý.
a) Nếu đồ thị có trọng số mà mỗi cạnh đều có trọng số là 1 thì bài toán trở thành tìm số các cạnh của đường đi ngắn nhất từ A đến F.
b) Các con số trong sơ đồ ở Hình 2.28 có thể là thời gian để đi dọc con đường đó, hoặc là chi phí khi đi hết con đường đó, ... Bởi vậy, ta có thể sử dụng thuật toán giải quyết bài toán gốc về bài toán tìm đường đi ngắn nhất để giải quyết bài toán tìm đường đi nhanh nhất hoặc đường đi có chi phí rẻ nhất, ...
2. BÀI TOÁN NGƯỜI ĐƯA THƯ
Bài toán người đưa thư phát biểu như sau: Một người đưa thư xuất phát từ bưu điện phải đi qua một số con đường để phát thư rồi quay lại điểm xuất phát, hỏi người đó phải đi như thế nào để đường đi là ngắn nhất. Ở đây các điểm cần phát thư nằm dọc theo các con đường cần phải đi qua.
Trong bài toán này, người đưa thư sẽ phải đi trên mỗi con đường ít nhất một lần (để phát được thư cho các điểm cần phát nằm dọc theo con đường đó) và cuối cùng quay lại vị trí xuất phát. Ngoài ra, cần đảm bảo quãng đường đi là nhỏ nhất có thể.
(Trang 47)
Trong ngôn ngữ của lí thuyết đồ thị, bài toán người đưa thư tương đương với bài toán tìm chu trình ngắn nhất đi qua tất cả các cạnh của một đồ thị cho trước.
Bài toán này có thể phát biểu dưới dạng một đồ thị có trọng số, ở đó đồ thị ứng với hệ thống các con đường, và trọng số của mỗi cạnh là độ dài của con đường tương ứng. Các cạnh của đồ thị này mô tả các con đường cần phải đi qua, các đỉnh của đồ thị là điểm đầu và cuối của các con đường đó (và có thể không phải là điểm cần phát thư). Khi đó ta cần tìm một chu trình có tổng trọng số nhỏ nhất và chứa mọi cạnh ít nhất một lần. Trong trường hợp tổng quát, nói chung đây là một bài toán khá phức tạp.
Trong một đồ thị liên thông (liên quan đến đồ thị có trọng số, liên thông):
1) Tất cả các đỉnh của đồ thị đều có bậc chẵn. Khi đó đồ thị có chu trình Euler và chu trình Euler đó chính là một đường đi yêu cầu.
2) Chỉ có hai đỉnh của đồ thị có bậc lẻ. Khi đó ta có thể tìm một đường đi Euler từ đỉnh bậc lẻ này đến đỉnh bậc lẻ kia, sau đó dùng thuật toán ở Mục 1 tìm đường đi ngắn nhất để quay trở lại đỉnh xuất phát. Kết hợp hai đường đi đó, ta được lời giải của bài toán đã cho.
Dưới đây ta xét hai ví dụ minh hoạ cho hai trường hợp này.
>Ví dụ 2. Cho đồ thị có trọng số như Hình 2.30. Chứng tỏ rằng đồ thị có chu trình Euler và hãy tìm một chu trình Euler xuất phát từ đỉnh A.
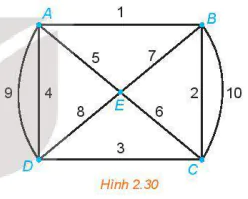
Giải
Vì đồ thị là liên thông và các đỉnh đều có bậc chẵn (ở đây là bậc 4) nên nó có chu trình Euler.
Một chu trình Euler xuất phát từ đỉnh A là ABDBECDEADA.
Chú ý. Nếu đồ thị có chu trình Euler thì độ dài quãng đường phải đi trong lời giải của bài toán người đưa thư chính là tổng các trọng số gắn trên các cạnh của đồ thị.
>Ví dụ 3. Một đồ thị có trọng số như Hình 2.31. Chứng tỏ đồ thị có trọng số của đồ thị là một chu trình ngắn nhất và chứa mọi cạnh ít nhất một lần.
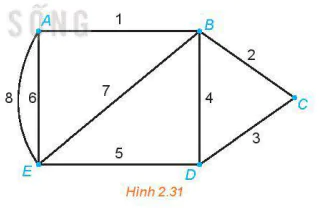
Giải
Đồ thị có hai đỉnh bậc lẻ là A và D nên ta có thể tìm được một đường đi Euler từ A đến D (đường đi này đi qua mỗi cạnh đúng một lần).
Một đường đi Euler từ A đến D là AEABEDBCD và tổng độ dài của nó là
6 + 8 + 1 + 7 + 5 + 4 + 2 + 3 = 36.
Để quay trở lại điểm xuất phát và có đường đi ngắn nhất, ta cần tìm một đường đi ngắn nhất từ D đến A theo thuật toán đã mô tả ở Mục 1.
Đường đi ngắn nhất từ D đến A là DBA và có độ dài là 4 + 1 = 5.
Vậy một chu trình cần tìm là AEABEDBCDBA và có độ dài là 36 + 5 = 41.
(Trang 49)
Chú ý. Trong lí thuyết đồ thị, người ta thường phát biểu bài của Ví dụ 2 dưới dạng: Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.31.
Từ đây về sau, ta cũng dùng cách phát biểu ngắn gọn như vậy.
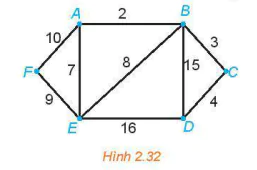
>Luyện tập. Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.32.
BÀI TẬP
2.15. Tìm đường đi ngắn nhất từ A đến D trong đồ thị có trọng số trên Hình 2.33.
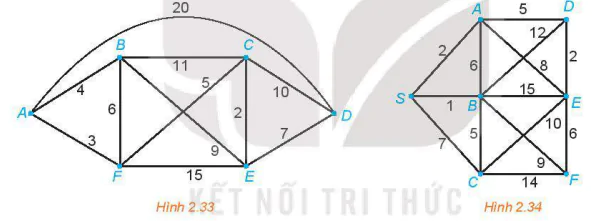
2.16. Tìm đường đi ngắn nhất từ đỉnh S đến mọi đỉnh khác của đồ thị có trọng số trên Hình 2.34.
2.17. Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.35.
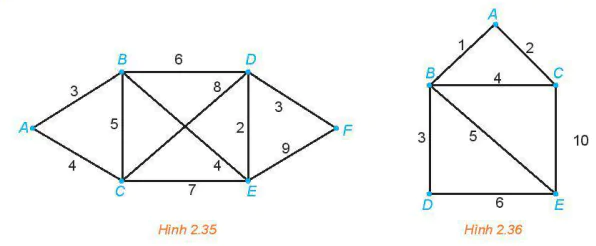
2.18. Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.36.






































































Bình Luận
Để Lại Bình Luận Của Bạn