Nội Dung Chính
(Trang 34)
Chuyên đề này giới thiệu một vài khái niệm cơ bản và kết quả ban đầu của lí thuyết đồ thị, một nhánh của toán học rời rạc có nhiều ứng dụng trong thực tế, và áp dụng giải quyết bài toán tìm đường đi tối ưu trong một vài trường hợp đơn giản.
| THUẬT NGỮ
| KIẾN THỨC, KĨ NĂNG
|
Khi vào một hội nghị, các đại biểu bắt tay nhau (hai người bắt tay nhau nhiều nhất 1 lần). Có một đại biểu không bắt tay ai hết và thầy rằng có 4 người bắt tay 4 lần, 5 người bắt tay 5 lần và 6 người bắt tay 6 lần. Nếu hội nghị có đúng 16 đại biểu thì ông ta đã đếm nhầm. Vì sao có thể kết luận như vậy?
Những kiến thức bạn đầu về lí thuyết đồ thị trong bài học này sẽ giúp chúng ta tìm được câu trả lời cho tình huống trên.
(Trang 35)
1. ĐỒ THỊ
a) Khái niệm đồ thị
>HĐ1. Nhận biết khái niệm đồ thị
Có bốn bạn học sinh khối 11 là An, Bình, Cường và Dung, trong đó: An là bạn của Bình và Cường, nhưng không là bạn của Dung; Dung là bạn của Cường, nhưng không là bạn của Bình, Bình là bạn của Cường.
a) Hãy biểu diễn mối quan An, Bình, Cường, Dung bằng một điểm trên mặt phẳng và dùng chữ cái đầu (in hoa) trong tên của họ để đặt tên cho các điểm này.
b) Nếu hai người là bạn của nhau, hãy nối các điểm biểu diễn tương ứng bằng một đoạn thẳng (hay đoạn đường cong).
c) Từ hình vẽ thu được ở HĐ1b, hãy cho biết: ai có nhiều bạn nhất và ai có ít bạn nhất?
Hình vẽ thu được ở HĐ1b (diễn tả mối quan hệ bạn bè giữa bốn học sinh đã cho) gọi là một đồ thị. Tổng quát ta có định nghĩa sau:
| Một đồ thị là một tập hợp hữu hạn các điểm (gọi là các đỉnh của đồ thị) cùng với tập hợp các đoạn đường cong hay thẳng (gọi là cạnh của đồ thị) có đầu mút tại các đỉnh của đồ thị. |
Chú ý. Theo định nghĩa của đồ thị, các cạnh của đồ thị thẳng hay cong, dài hay ngắn, các đỉnh ở vị trí nào đều không quan trọng, mà bản chất là đồ thị có bao nhiêu đỉnh, bao nhiêu cạnh và đỉnh nào được nối với đỉnh nào.
| Ta thường kí hiệu V(G) là tập hợp các đỉnh và E(G) là tập hợp các cạnh của đồ thị G, và viết G = (V, E). Cạnh nối hai đỉnh A và B thường được kí hiệu là AB hoặc BA, và khi đó A và B gọi là hai đỉnh kề nhau. Nếu hai đầu mút của cạnh trùng nhau tại đỉnh C thì ta gọi cạnh ấy là một khuyên, kí hiệu là CC. Hình 2.1 cho ta một đồ thị có 4 đỉnh là A, B, C, D và 5 cạnh là AB, AC, AD, BC và CC. | 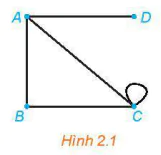 |
>Ví dụ 1. Viết tập hợp các đỉnh và tập hợp các cạnh của đồ thị G trong Hình 2.2.
Giải
| Tập hợp các đỉnh của đồ thị G là V(G) = {A, B, C, D}. Tập hợp các cạnh của đồ thị G là E(G) = {AB, AC, BC, CD}. | 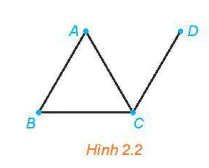 |
(Trang 36)
>Luyện tập 1. Bảng sau với giải bóng đá thế giới World Cup 2018 gồm bốn đội: Đức, Hàn Quốc, Mexico và Thụy Điển. Biểu diễn các đội này bằng các điểm phân biệt kí hiệu lần lượt là Đ, H, M, T (vẽ sao cho không có ba điểm nào thẳng hàng để dễ quan sát) và nếu hai đội nào đấu với nhau thì ta nối hai điểm tương ứng bằng một đoạn thẳng, ta sẽ được một đồ thị G.
Viết tập hợp các đỉnh và tập hợp các cạnh của đồ thị G.
b) Đơn đồ thị và đa đồ thị
>HĐ2. Nhận biết khái niệm đơn đồ thị.
Xét đồ thị cho trong Hình 2.2.
a) Đồ thị trên có khuyên không?
b) Có hai đỉnh nào của đồ thị được nối với nhau bằng nhiều hơn một cạnh không?
| Một đồ thị không có khuyên, trong đó hai đỉnh được nối bằng nhiều nhất một cạnh (không có hai cạnh cùng nối một cặp đỉnh) gọi là một đơn đồ thị. Một đồ thị có khuyên, trong đó hai đỉnh có thể nối bằng nhiều cạnh, gọi là một đa đồ thị. |
Chú ý. Trong cuốn sách này, khi chỉ nói từ "đồ thị" thì ta hiểu là đơn đồ thị. Khi nào cần xét đa đồ thị thì ta sẽ nói rõ.
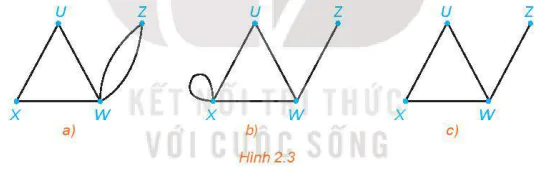
>Ví dụ 2. Hình nào sau đây biểu diễn một đơn đồ thị? Một đa đồ thị?
Giải
Hình a) không có khuyên và có hai cạnh nối hai đỉnh Z và W, nên là một đa đồ thị.
Hình b) có khuyên nên không phải là đơn đồ thị, cũng không phải là đa đồ thị.
Hình c) không có khuyên và hai đỉnh chỉ được nối bằng nhiều nhất một cạnh nên là một đơn đồ thị.
>Luyện tập 2. Vẽ đồ thị G với các đỉnh và các cạnh như sau:
V(G) = {U, W, X, Z} và E(G) = {UW, WX, WZ, XZ}.
G có phải là một đơn đồ thị không?
c) Đồ thị đầy đủ
>HĐ3. Nhận biết đồ thị đầy đủ
Xét đồ thị nhận được trong Luyện tập 1. Có cặp đỉnh nào của đồ thị này mà không có cạnh nối chúng không?
(Trang 37)
| Một đồ thị là đầy đủ khi và chỉ khi mỗi cặp đỉnh của nó đều được nối bằng một cạnh. |
Nhận xét. Một đồ thị đầy đủ là đồ thị mà mọi cặp đỉnh của nó đều kề nhau. Một đồ thị đầy đủ hoàn toàn được xác định bởi số đỉnh của nó. Đồ thị đầy đủ có n đỉnh thường được kí hiệu là Kn.
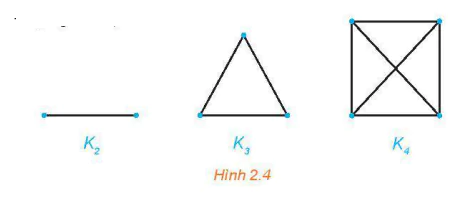
>Ví dụ 3. Vẽ các đồ thị đầy đủ K2, K3 và K4.
Giải
Ta có các đồ thị K2, K3 và K4 như Hình 2.4.
>Luyện tập 3. Vẽ các đồ thị đầy đủ có 5 đỉnh, có 6 đỉnh.
2. BẬC CỦA ĐỈNH
>HĐ4. Nhận biết bậc của đỉnh
Cho đồ thị như Hình 2.5. Tìm các đỉnh là đầu mút của: 0 cạnh; 1 cạnh; 2 cạnh; 3 cạnh.
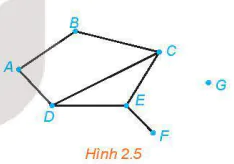
| Một đỉnh của đồ thị được gọi là đỉnh bậc n nếu nó là đầu mút của n cạnh. |
Chú ý. Đỉnh bậc 0 gọi là đỉnh cô lập. Đỉnh bậc 1 gọi là đỉnh treo.
Trong đồ thị ở Hình 2.5, D là đỉnh bậc 3, F là đỉnh treo, G là đỉnh cô lập.
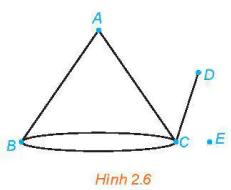
>Ví dụ 4. Xác định bậc của các đỉnh của đồ thị ở Hình 2.6.
Giải
A là đỉnh bậc 2, B là đỉnh bậc 3, C là đỉnh bậc 4, D là đỉnh bậc 1, E là đỉnh bậc 0.
Ta có thể chứng minh định lí (gọi là Định lí bắt tay) sau đây:
| Trong mọi đồ thị G, tổng tất cả các bậc của các đỉnh là một số chẵn và bằng hai lần tổng tất cả các cạnh của G. |
(Trang 38)
Hệ quả. Số đỉnh bậc lẻ là một số chẵn.
>Ví dụ 5. Cho đồ thị G có 14 đỉnh và 25 cạnh. Biết rằng mỗi đỉnh của đồ thị G đều có bậc 3 hoặc bậc 5. Hỏi G có bao nhiêu đỉnh bậc 3?
Giải
Gọi x là số đỉnh bậc 3. Khi đó số đỉnh bậc 5 của G là 14 – x. Tổng tất cả các bậc của đỉnh là 3x + 5(14 – x).
Vì đồ thị có 25 cạnh nên ta có: 3x + 5(14 – x) = 2.25 = 50 ⇔ 2x = 20 ⇔ x = 10. Vậy đồ thị G có 10 đỉnh bậc 3.
>Ví dụ 6. Hãy giải bài toán trong tình huống mở đầu.
Giải
Ta vẽ một đồ thị với 16 đỉnh tương ứng với 16 đại biểu tham dự hội nghị. Nếu hai đại biểu bắt tay nhau thì ta nối hai đỉnh tương ứng bằng một cạnh.
Theo số liệu mà đại biểu đếm số bắt tay cung cấp, ta có một đồ thị với 16 đỉnh, trong đó có 1 đỉnh bậc 0, 4 đỉnh bậc 4, 5 đỉnh bậc 5 và 6 đỉnh bậc 6.
Ở đây số đỉnh bậc 5 là 5, là một số lẻ. Điều này mâu thuẫn với hệ quả của Định lí bắt tay. Vậy đại biểu đó đã đếm sai.
>Luyện tập 4. Chứng minh rằng không có đơn đồ thị với 12 đỉnh và 28 cạnh mà các đỉnh đều có bậc 3 hoặc 4.
3. ĐƯỜNG ĐI VÀ CHU TRÌNH
a) Khái niệm đường đi và chu trình
>HĐ5. Nhận biết khái niệm đường đi và chu trình
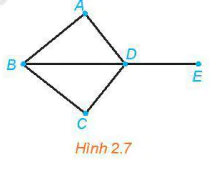
Cho đồ thị như Hình 2.7. Bằng cách đi đọc theo các cạnh, với điều kiện không đi qua cạnh nào quá một lần (có thể có cạnh không cần đi qua), hãy chỉ ra các cách để:
a) Đi từ đỉnh A đến đỉnh E.
b) Đi từ đỉnh A và lại quay về đỉnh A.
| Trong một đồ thị G, một dãy cạnh nối tiếp (hai cạnh nối tiếp là hai cạnh có chung đầu mút) AB, BC, CD, ..., MN_ được gọi là một đường đi nối A với P, kí hiệu là ABCD... MNP. Điểm A gọi là đầu đường, điểm P gọi là cuối đường. Một đường đi khép kín (đầu đường trùng với cuối đường) gọi là một chu trình. Một đường đi (chu trình) qua n cạnh gọi là một đường đi (chu trình) có độ dài n. Một đường đi (hay chu trình) là sơ cấp nếu nó không đi qua đỉnh nào hai lần trở lên. Một đường đi (chu trình) là đơn giản nếu nó không đi qua cạnh nào hai lần trở lên. |
(Trang 39)
| >Ví dụ 7. Cho đồ thị đầy đủ có 4 đỉnh Hình 2.8. Tìm những chu trình sơ cấp xuất phát từ đỉnh A và có độ dài 3, độ dài 4. Giải Những chu trình sơ cấp có độ dài 3 xuất phát từ đỉnh A là: ABCA, ADBA, ACBA, ADCA, ABDA, ADDA. Những chu trình sơ cấp có độ dài 4 xuất phát từ đỉnh A là: ABDCA, ADCBA, ACDBA, ADBCA, ADCBA. | 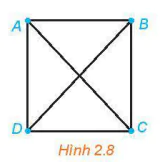 |
| >Luyện tập 5. Cho đồ thị đầy đủ có 5 đỉnh như Hình 2.9. Tìm những chu trình sơ cấp xuất phát từ đỉnh A và có độ dài 4; độ dài 5. | 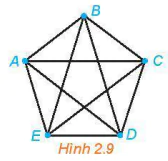 |
b) Tính liên thông của đồ thị
| >HĐ6. Nhận biết tính liên thông của đồ thị Trong đồ thị ở Hình 2.10, hãy: a) Tìm một đường đi từ đỉnh A đến đỉnh E. b) Có tồn tại một đường đi từ đỉnh A đến đỉnh F hay không? | 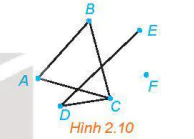 |
| Hai đỉnh A và B của một đồ thị gọi là liên thông nếu có một đường đi nối A và B. Một đồ thị G gọi là liên thông nếu mọi cặp đỉnh của G là liên thông. Một cạnh CD của đồ thị G gọi là cầu nếu khi bỏ cạnh CD thì hai đỉnh C và D không còn liên thông nữa. Một đồ thị G không liên thông đều được chia thành một số đồ thị (gọi là đồ thị con của G) liên thông, rời nhau, mỗi đồ thị con đó gọi là một thành phần liên thông của G. |
| >Ví dụ 8. Tìm các thành phần liên thông của đồ thị trong Hình 2.11. Giải Đồ thị ở Hình 2.11 có hai thành phần liên thông: một thành phần gồm 3 đỉnh A, B, C và các cạnh AB, AC, BC; một thành phần gồm hai đỉnh D, E và cạnh DE. | 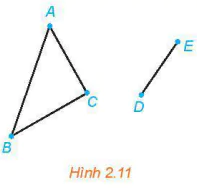 |
Người ta chứng minh được rằng:
| Một đồ thị có 2n đỉnh, mỗi đỉnh có bậc ít nhất bằng n, là đồ thị liên thông. |
>Ví dụ 9. Giả sử một lớp có 40 học sinh. Biết rằng mỗi em có số điện thoại ít nhất là 20 bạn trong lớp và nếu bạn A có số điện thoại của bạn B thì bạn B cũng có số điện thoại của bạn A. Chứng minh rằng bất cứ hai em nào trong lớp cũng có số điện thoại của nhau.
(Trang 40)
| Giải Ta đặt tương ứng mỗi học sinh trong lớp với một đỉnh của đồ thị và hai đỉnh được gọi là liên thông nếu hai em có số điện thoại của nhau. Bài toán trở thành: Cho một đồ thị có 40 đỉnh. Biết mỗi đỉnh bậc ít nhất là 20 đỉnh khác. Chứng minh rằng đồ thị là liên thông. Đồ thị này có 40 đỉnh, mỗi đỉnh có bậc ít nhất là 20, do đó đồ thị là liên thông. Vậy, bất cứ hai em học sinh nào trong lớp cũng có số điện thoại của nhau. | 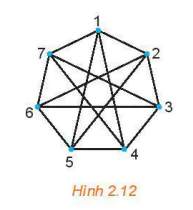 |
>Luyện tập 6. Chứng minh đồ thị ở Hình 2.12 là liên thông. Hãy chỉ ra một đường đi nối 1 và đỉnh 6.
BÀI TẬP
2.1. Cho hình biểu diễn của đồ thị G với tập đỉnh V(G) = {1; 2; 3; 4; 5} và tập cạnh
E(G) = {12; 14; 23; 25; 34; 35}.
Đồ thị G có phải là đơn đồ thị không? Có phải là đồ thị đầy đủ không?
2.2. Hãy vẽ một đồ thị có 4 đỉnh và:
a) có đúng hai đỉnh cùng bậc và bậc là 1;
b) có đúng hai đỉnh cùng bậc và bậc là 2.
2.3. Một đồ thị con của đồ thị G là một đồ thị mà mọi đỉnh của nó đều là đỉnh G và mọi cạnh của nó cũng là cạnh của G.
Những đồ thị nào trong các hình a), b), c) dưới đây là đồ thị con của đồ thị G?
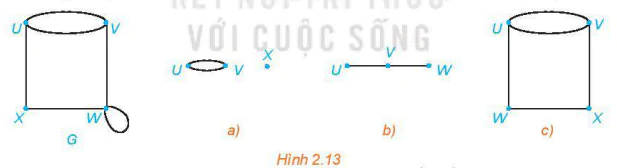
2.4. Chứng minh rằng một đồ thị đầy đủ có n đỉnh thì có 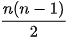 cạnh.
cạnh.
2.5. Chứng minh rằng không tồn tại đồ thị với các đỉnh có bậc là 2, 3, 3, 4, 4 và 5.
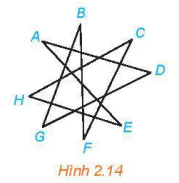
2.6. Cho đồ thị G như Hình 2.14.
a) Tìm một đường đi từ đỉnh A đến đỉnh B.
b) G có liên thông không?
c) Trong G có chu trình sơ cấp nào không?







































































Bình Luận
Để Lại Bình Luận Của Bạn