Nội Dung Chính
(Trang 41)
| THUẬT NGỮ
| KIẾN THỨC, KĨ NĂNG
|
Trong lí thuyết đồ thị, bài toán Bảy cây cầu ở Königsberg (nay là thành phố Kaliningrad, nước Nga) được phát biểu như sau: Thành phố có 7 cây cầu bắc qua sông như Hình 2.15a dưới đây; có thể nào đi dạo khắp các cây cầu nhưng mỗi cầu chỉ đi qua một lần không?
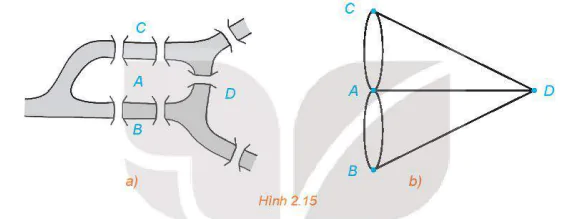
Nếu ta coi mỗi khu vực A, B, C, D của thành phố là một đỉnh, mỗi cầu qua lại hai khu vực như một cạnh nối hai đỉnh, thì bản đồ thành phố Königsberg là một đồ thị như Hình 2.15b. Vấn đề đặt ra chính là: Có thể đi được Hình 2.15b mà mỗi cạnh chỉ đi qua một lần không?
1. ĐƯỜNG ĐI EUCLER
a) Khái niệm đường đi Euler
>HĐ1. Nhận biết đường đi Euler
Hãy thử vẽ mỗi hình trong Hình 2.16 bằng một nét liền.
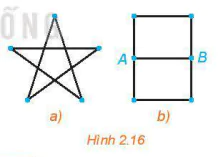
| Cho một đồ thị G. Một đường đi từ đỉnh A đến đỉnh B và chứa mọi cạnh của G được gọi là một đường đi Euler từ A đến B. Một chu trình đơn giản chứa mọi cạnh của G được gọi là một chu trình Euler của G. |
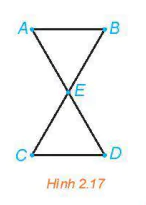
>Ví dụ 1. Tìm một chu trình Euler của đồ thị trong Hình 2.17
Giải
Một chu trình Euler của đồ thị là ABCDEA.
(Trang 42)
Định lí sau đây cho ta một điều kiện cần và đủ để một đồ thị có chu trình Euler.
Định lí 1 (Euler)
| Một đồ thị G có một chu trình Euler khi và chỉ khi G liên thông và mọi đỉnh của G đều có bậc chẵn. |
Từ Định lí 1 ta có thể chứng minh định lí sau.
Định lí 2
| Một đồ thị G có một đường đi Euler từ A đến B khi và chỉ khi G liên thông và mọi đỉnh của G đều có bậc chẵn, trừ A và B có bậc lẻ. |
Chú ý. Hai định lí trên cũng đúng cho trường hợp G là đơn đồ thị.
| >Ví dụ 2. Giải thích vì sao trong Hình 2.18: a) Các hình a) và b) có thể vẽ được bằng một nét liền; b) Các hình c) và d) không thể vẽ được bằng một nét liền. |  |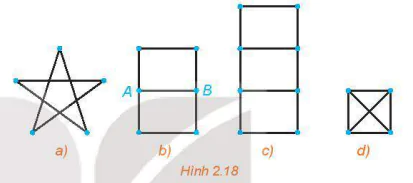
Giải
Đồ thị ở hình a) là liên thông và các đỉnh đều có bậc chẵn (ở đây là bậc bằng 2) nên nó có chu trình Euler. Đồ thị ở hình b) là liên thông và chỉ có đúng hai đỉnh bậc lẻ (ở đây là bậc bằng 3) nên nó có đường đi Euler. Vì vậy ta có thể vẽ cách hình a) và b) bằng một nét liền.
Các đồ thị hình c) và d) có bốn đỉnh bậc lẻ (ở đây là bậc bằng 3) nên chúng không có chu trình Euler và cũng không có đường đi Euler. Vì vậy ta không thể vẽ các hình c) và d) bằng một nét liền.
>Ví dụ 3. Giải bài toán trong tình huống mở đầu.
Giải
Xét đồ thị G ở Hình 2.15b. Vì các đỉnh A, B, C, D đều có bậc lẻ nên theo Định lí 2, G không có đường đi Euler (và không có chu trình Euler).
Vậy không thể nào đi dạo qua khắp các cây cầu của thành phố Königsberg nhưng mỗi cầu chỉ đi qua một lần.
>Luyện tập 1. Đồ thị nào dưới đây có một đường đi Euler? Hãy chỉ ra một đường đi Euler của nó.
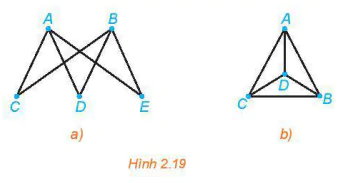
(Trang 43)
2. ĐƯỜNG ĐI HAMILTON
>HĐ2. Nhận biết đường đi Hamilton
| Có 5 thành phố du lịch A, B, C, D, E và các con đường nối các thành phố này như Hình 2.20. Hãy chỉ ra một cách để đi tham quan cả 5 thành phố đó, mà không cần đến địa điểm nào quá một lần. |  |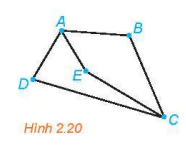
| Một đường đi sơ cấp từ đỉnh A đến đỉnh B và qua mọi đỉnh của đồ thị G được gọi là một đường đi Hamilton từ A đến B. Một chu trình sơ cấp chứa mọi đỉnh của G được gọi là một chu trình Hamilton của G. |
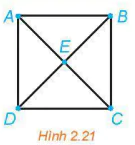
>Ví dụ 4. Tìm một chu trình Hamilton của đồ thị trên Hình 2.21.
Giải
Một chu trình Hamilton của đồ thị là ABCDEA.
Định lí sau đây cho ta một điều kiện đủ cho sự tồn tại chu trình Hamilton.
Định lí 3 (Ore)
| Nếu G là đơn đồ thị có n đỉnh (n ≥ 3) và mỗi cặp đỉnh không kề nhau đều có tổng bậc không nhỏ hơn n thì G có một chu trình Hamilton. |
Hệ quả (Định lí Dirac). Nếu G là đơn đồ thị có n đỉnh (n ≥ 3) và mọi đỉnh có bậc không nhỏ hơn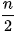 
thì G có một chu trình Hamilton.
Từ định lí Dirac ta chứng minh được:
Định lí 4
Nếu đơn đồ thị G có n đỉnh (n ≥ 3) và mọi đỉnh có bậc không nhỏ hơn 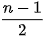 thì G có một đường đi Hamilton. |
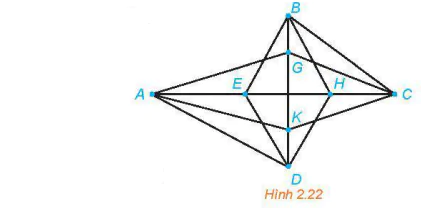
>Ví dụ 5. Đồ thị Hình 2.22 có chu trình Hamilton không? Nếu có, hãy chỉ ra một chu trình Hamilton xuất phát từ đỉnh A.
Giải
Đồ thị có 8 đỉnh, mọi đỉnh đều có bậc là 4. Do đó, theo Định lí Dirac, đồ thị có một chu trình Hamilton.
Có thể thấy một chu trình Hamilton xuất phát từ đỉnh A là: AGCKDHBEA.
Chú ý. Trong một số trường hợp đơn giản, ta có thể tìm đường đi (chu trình Hamilton) của G hoặc chúng minh G không có đường đi (chu trình Hamilton) dựa vào nhận xét sau: Đường đi (chu trình) Hamilton phải đi qua các cạnh có độ dài tổng nhỏ bậc 2.
(Trang 44)
| >Luyện tập 2. Đồ thị nào trong Hình 2.23 có đường đi Hamilton? Hãy chỉ ra một đường đi Hamilton của nó. |  |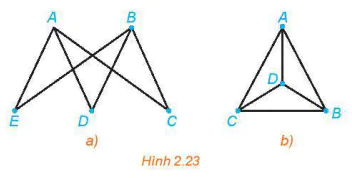
BÀI TẬP
2.7. Mỗi đồ thị sau có một chu trình Euler hoặc một chu trình Hamilton không? Hãy vẽ một chu trình Euler hoặc một chu trình Hamilton khi có thể.
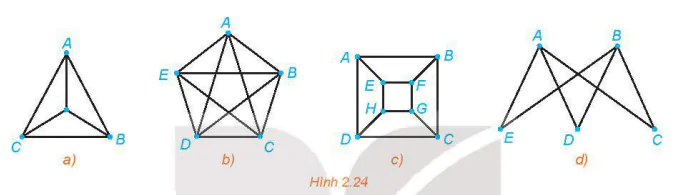
2.8. Có thể nào đi dạo qua các cây cầu trong Hình 2.25, mỗi cây cầu vừa đúng một lần?
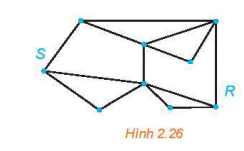
2.9. Cho đồ thị G như Hình 2.26. Tìm một chu trình Hamilton xuất phát từ đỉnh S của G.
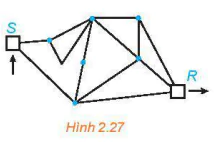
2.10. Cho đồ thị G như Hình 2.27. Tìm một đường đi Hamilton từ S đến R.
(Trang 45)
2.11. Hãy chỉ ra một ví dụ chứng tỏ rằng điều kiện bậc của mỗi đỉnh của đồ thị G không nhỏ hơn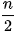 
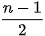" 2.12. a) Giả sử G là một đồ thị với n đỉnh và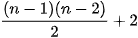 
cạnh. Sử dụng Định li Ore, hãy chứng minh G có một chu trình Hamilton.
b) Tìm một đồ thị với n đỉnh và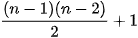 
cạnh mà không có chu trình Hamilton.
2.13. Với giá trị nào của n thì đồ thị đầy đủ Kn có một chu trình Euler? Có một đường đi Euler?
2.14. Với giá trị nào của n thì đồ thị đầy đủ Kn có một chu trình Hamilton? Có một đường đi Hamilton?
| Em có biết? Euler và lí thuyết đổ thị Leonhard Euler (1707 - 1783) là một trong những nhà toán học vĩ đại nhất trong lịch sử. Ông đã có những khám phá quan trọng và đóng góp tiên phong trong nhiều chuyên ngành toán học. Ông cũng giới thiệu nhiều thuật ngữ và kí hiệu toán hiện đại, được dùng phỗ biến ngày nay như kí hiệu số e dùng làm cơ số cho logarit tự nhiên, kí hiệu f(x) cho hàm số, kí hiệu các hàm lượng giác, kí hiệu Σ để chỉ tổng, ... Một nhận xét của nhà toán học người Pháp Laplace đã thể hiện ảnh hưởng của Euler đối với toán học: “Hãy đọc Euler, đọc Euler đi, ông ấy là bậc thẩy của tất cả chúng ta."
Leonhard Euler (1707-1783), nhà toán học người Thuy Sĩ Bài báo của Euler về lời giải bài toán Bảy cây cầu Königsberg, xuất bản năm 1736, được coi là công trình đầu tiên về thuyệt đồ thị. Một trong những bài toán nồi tiếng và thủ vị nhất của lí thuyết đồ thị là bài toán bốn màu: “Liệu rằng chỉ với bốn màu có thể tô màu một bản đồ bất kì sao cho không có hai nước nào cùng biên giới được tô cùng màu hay không?" Bài toán này được đề xuất bởi Francis Guthrine năm 1852, và chỉ được giải sau gần một thế kỉ vào năm 1976 bởi Kenneth Appel và Wolfgang Haken, với lời giải dựa vào sự hỗ trợ của máy tính. Trong khi cố gắng giải quyết bài toán này, các nhà toán học đã phát minh ra nhiều thuật ngữ và khái niệm nền tảng cho lí thuyết đồ thị. Đồ thị biều diễn được rất nhiều cấu trúc, nhiều mối quan hệ và quá trình trong các hệ vật lí, sinh học, quan hệ xã hội, hệ thống thông tin, mạng lưới giao thông,... và do đó ngày nay lí thuyết đồ thị được nghiên cứu rất mạnh mẽ và có nhiều ứng dụng thực tế quan trọng. Một vài bài toán về tìm đường đi trong thực tế như bài toán tìm đường đi tối ưu (ngắn nhất, nhanh nhất, có chi phí rẻ nhất,...) trong những tình huống đơn giản sẽ được nghiên cứu ở bài học sau. (Theo scienceworld.wolfram.com) |
Các Bài Học Khác
Chuyên đề học tập Toán 11 - Bài 10: Bài Toán Tìm Đường Đi Tối Ưu Trong Một Vài Trường Hợp Đơn Giản - Tìm hiểu các phương pháp xác định đường đi ngắn nhất hoặc hiệu quả nhất trong những đồ thị đơn giản.
Xem thêm ⟶
Bình Luận
Để Lại Bình Luận Của Bạn