Nội Dung Chính
(Trang 21)
| THUẬT NGỮ
| KIẾN THỨC, KĨ NĂNG
|
| Bằng quan sát, ta có cảm nhận rằng ba hình a), b), c) bằng nhau. Nếu cắt giấy, lấy rằng ba tường hình thì ta có hình b) và c) với nhau, hay up khít hai hình a) và c) vào nhau đối tượng toán học nào cho phép ta biến đạt hai hình bằng nhau? Hãy cùng tìm hiểu trong bài học này. |  |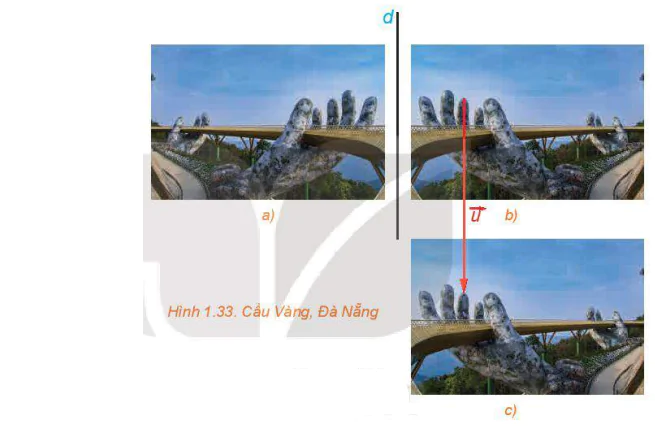
>HĐ. Các phép tịnh tiến, phép đối xứng trục, phép quay cùng có tính chất nào trong các tính chất sau?
a. Biển một vectơ thành vecto bằng nó.
b. Biến một đường tròn thành một đường tròn cùng tâm.
c. Biến một đoạn thằng thành đoạn thẳng bằng nó.
d. Biến một đường thẳng thành đường thẳng song song với nó.
| Phép biến hình f được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm bất kì. |
Chú ý
- Ta có thể chứng minh được rằng, phép dời hình biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính và có tâm là ảnh của tâm, biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự của chúng, biến đường thẳng thành đường thẳng.
- Hai hình H và H' được gọi là bằng nhau, nếu có phép dời hình biến hình H thành H'.
- Phép tịnh tiến, phép đối xứng trục, phép quay, phép đối xứng tâm đều bảo toàn khoảng cách nên chúng là các phép dời hình.
(Trang 22)
>Ví dụ 1. Trong mặt phằng toạ độ Oxy, gọi f là phép biến hình biến mỗi điểm có toạ độ (х; у) thành điểm có toạ độ (-х; y +1).
a) Chứng minh rằng f là một phép dời hình.
b) Chứng minh rằng với mọi điểm M, nếu f biến M thành M' thì M khác М'.
c) f có là phép nào trong các phép đối xứng trục, phép quay, phép tịnh tiến hay không?
Giải
a) Hai điểm bất kì M(x; y), N(x'; y') có ảnh qua f tương ứng là M'(−x; y + 1), N'(-x'; y'+ 1).
Khi đó
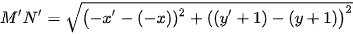
Do đó, f là một phép dời hình.
b) Phép dời hình fbiến điểm M(x; y) thành điểm có toạ độ M'(-x; y + 1). Do y ≠ y +1 nên M khác M'
c) Vì phép đối xứng trục biến mỗi điềm trên trục đối xứng thành chính nó và phép quay biến tâm quay thành chính nó, nên từ b) ta có f không thể là phép đối xứng trục hay là phép quay.
Các điểm O(0; 0), A(1; 0) tương ứng có ảnh là O'(0; 1), A'(-1; 1).
Ta có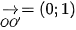 
, 
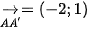. Do 
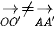nên f không thể là phép tịnh tiến.
Vậy mặc dù f là một phép dời hình, nhưng nó không phải là phép tịnh tiến, phép đối xứng trục, phép quay.
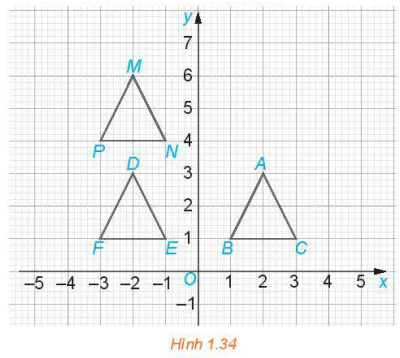
>Luyện tập. Trong mặt phẳng toạ độ Oxy ở Hình 1.34, gọi flà phép biến hình biến mỗi điểm có toạ độ (x; y) thành điểm có toạ độ (-x; y +3). Trong các khẳng định sau, những khằng định nào đúng.
a) f biến 
DEF. b) f biến DEF thành MNP
c) f biến ABC thành
(Trang 23)
Chú ý
- Phép biến hình f trong Luyện tập trên có được bằng cách thực hiện liên tiếp phép đối xứng trục Oy và phép tịnh tiến theo vecto
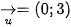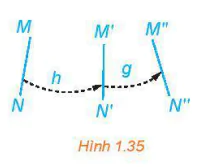
. - Thực hiện liên tiếp hai phép dời hình h và g (h trước, g sau) ta cũng được một phép dời hình, tức là, nếu h biến mỗi điềm M thành điểm M', g biến điểm M' thành M", thì phép biến hình biến mỗi điềm M thành điểm M" cũng là một phép dời hình (H.1.35).
>Ví dụ 2. Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Một đường thẳng đi qua O (khác đường chéo) cắt các cạnh AB, CD tương ứng tại M, N (H.1.36). Chứng minh rằng hai tứ giác AMND và CNMB bằng nhau.
Giải
| Ta có O là trung điềm của các đường chéo AC và BD. Ta có Do đó Phép đối xứng tâm O biến các điềm A, M, N, D tương ứng thành các điềm C, N, M, B, do đó biến tứ giác AMND thành tứ giác CNMB. Vậy hai tứ giác AMND và CNMB bằng nhau. |  |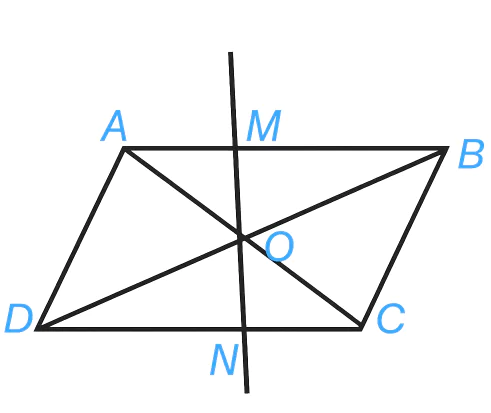
, AO = CO, 
ОАМ = >Vận dụng. Trong tình huống mở đầu, bằng quan sát (H.1.33), hãy chỉ ra phép dời hình:
a) Biến Hình a) thành Hình b).
b) Biến Hình b) thành Hình c).
c) Biến Hình a) thành Hình c).
d)Biển Hình c) thanh Hinh a).
BÀI TẬP
1.16. Trong mặt phẳng toạ độ Oxy, cho vecto u = (0; 1). Những khẳng định nào trong các khẳng định sau là đúng?
a) Phép đối xứng trục Oy biến mỗi điểm M (x; y) thành điểm M'(-x; y).
b) Phép tịnh tiến theo vectơ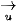 
biến điểm M'(-x; y) thành điểm M"(-x; y + 1).
c) Thực hiện liên tiếp hai phép dời hình ĐOy và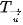 
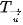sau) ta được phép dời hình biến mỗi điểm M(x; y) thành điểm M"(-х; y + 1). d) Phép dời hình có được bằng cách thực hiện liên tiếp hai phép dời hình ĐOy và 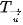biến điểm A(1; 2) thành điểm A"(–1; 1).
1.17. Bằng quan sát, hãy chỉ ra trong mỗi hình trong Hình 1.37 một phép dời hình biến hình vuông thành hình vuông A', đồng thời biến hình bình hành B thành hình bình hành B'.
(Trang 24)
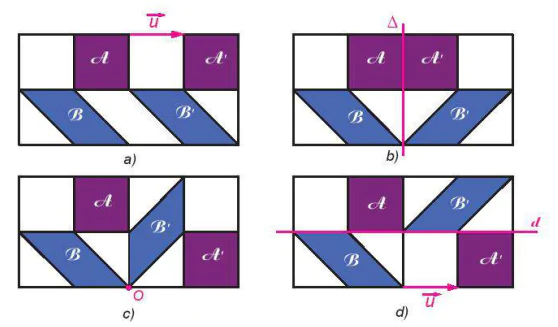
Hình 1.37
1.18. Cho một mảnh giấy hình thang cân ABCD (AB // CD). Hãy chỉ ra một cách cắt mảnh giấy đó thành hai mảnh giấy bằng nhau.
| 1.19. Hình 1.38 được vẽ dựa theo bức tranh Kị binh (horsmen) của Escher, gồm các hình bằng nhau mô tả các kị binh trên ngựa. Bằng quan sát, hãy chỉ ra những khẳng định đúng trong các khẳng định sau. a) Có phép tịnh tiến biến mỗi chiến binh thành một chiến binh cùng màu. b) Có phép đối xứng trục biến mỗi chiến binh thành một chiến binh khác màu. c) Có phép dời hình có được bằng cách thực hiện liên tiếp một phép đối xứng trục và một phép tịnh tiến biến mỗi kị binh thành một kị binh khác màu. |
Hình 1.38 |
| Em có biết? Tại các quảng trường, con phố du lịch của thành phố Lisbon (Bồ Đào Nha) hay lâu đài Alhambra (Tây Ban Nha), ta bắt gặp rất nhiều kiểu lát gạch, khảm trang trí nghệ thuật, trông đẹp mắt và thú vị. |
Hình 1.39. Quảng trường Rossio, Lisbon |
(Trang 25)
| Trong mỗi phép lát mặt phẳng (không giới hạn) bởi các viên gạch bằng nhau, ta có thể nhìn mỗi viên gạch là ảnh của viên gạch khác qua một phép dời hình (vì các viên gạch bằng nhau). Rõ ràng, người thợ sẽ có thể yên tâm tuần tự lát các viên gạch mà không sợ đến một lúc nào đó buộc phải cắt gạch nếu anh ta được cung cấp một "túi" các phép dời hình để cách khi đặt viên gạch thứ nhất anh ta chỉ việc lần lượt đặt các viên tiếp theo là ảnh của viên đã tiền qua các phép dời hình thuộc "túi" đó. Năm 1891, Fedorov đã chứng minh được rằng có tất cả 17 loại "túi" cho phép lát kín mặt phẳng mà không cần cắt gạch. Một điều khá thú vị là cả 17 cách lát mà toàn học chứng minh được đều đã được con người thực hiện trước đó rải rác ở nhiều nơi trên thế giới (Theo A.B.Sosinsky, GEOMETRIES). Để có thể thực hiện thành công việc lát mặt phẳng, rõ ràng người thợ đã "hành động địa phương" nhưng "tư duy toàn cục" (Khẩu hiệu "Think globally, act locally" được dùng trong nhiều lĩnh vực như môi trường, quy hoạch, giáo dục,...). Các phép dời hình trong mỗi việc lát còn mang đến cho người ngắm hứng khám phá và tạo nên sự chuyển động cho hình ảnh tổng thể. Nếu yêu cầu "túi" chỉ gồm phép tịnh tiến và phép quay thì có đúng 5 loại "túi" đảm bảo cho việc lát, ứng với 5 cách lát bên.
|
Các Bài Học Khác
Chuyên đề học tập Toán 11 - Bài 6: Phép Vị Tự - Trang bị kiến thức về phép vị tự, giúp hiểu rõ cách một hình được phóng đại hoặc thu nhỏ từ một tâm cố định.
Xem thêm ⟶
Chuyên đề học tập Toán 11 - Bài 7: Phép Đồng Dạng - Giới thiệu phép biến hình giữ nguyên hình dạng, có thể thay đổi kích thước, là sự kết hợp của dời hình và vị tự.
Xem thêm ⟶
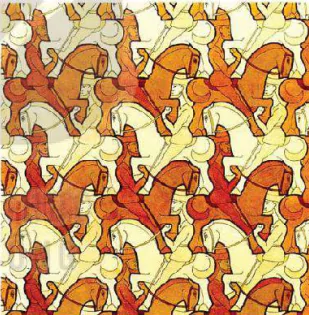
Bình Luận
Để Lại Bình Luận Của Bạn