Nội Dung Chính
(Trang 12)
| THUẬT NGỮ
| KIẾN THỨC, KĨ NĂNG
|
| Trong tự nhiên, cuộc sống, Toán học, Kiến trúc và Hội hoạ, ta bắt gặp nhiều hình ảnh cân đối. Sự cân đối có thể mang lại vẻ đẹp, làm nên sự vững chắc và nhiều điều ý nghĩa khác, có lớp ý nghĩa biến nhận ra các hình ảnh hai chiều có trục đối xứng. Bài học này cho phép ta diễn đạt chính xác và rõ ràng hơn về chúng. |
Nhà Rông Tây Nguyên (Ảnh: dantocmiennui.vn) |
1. PHÉP ĐỐI XỨNG TRỤC
| > HĐ1. Cầu Ponte Sisto in hình dưới dòng sông Tiber, tạo nên một hình ảnh có tính đối xứng trục. a) Hãy chỉ ra trục đối xứng của hình ảnh đó. b) Có thể đếm được bao nhiêu hình bóng điện dưới dòng sông? Mỗi hình đó là ảnh của hình bóng điện của bóng điện nào trên cầu? |
Cầu Ponte Sisto & Thủ đô Rome của nước Ý |
| Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó và biến mỗi điểm M không thuộc d thành điểm M' sao cho d là đường trung trực của đoạn thẳng MM' được gọi là phép đối xứng trục d, kí hiệu Đd. | 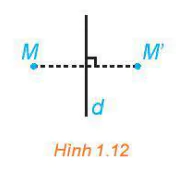 |
(Trang 13)
Chú ý
| Nếu M' là ảnh của M qua Đd thì M cũng là ảnh của M' qua Đd. Do đó, nếu hình 7đ' là ảnh của hình |  |
| Hình |
Hình 1.13 |
>Ví dụ 1. Trong mặt phẳng toạ độ Oxy, tim toạ độ ảnh của các điểm M(3; 4), N(-1;2), qua phép đối xứng trục
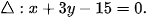
Giải
Toạ độ của điểm M(3; 4) thoả mãn phương trình đường thẳng  . Do đó, M(3; 4) thuộc A và có ảnh qua phép đối xứng trục
. Do đó, M(3; 4) thuộc A và có ảnh qua phép đối xứng trục  chính là M(3; 4).
chính là M(3; 4).
Điểm N (-1; 2) không thuộc A. Gọi N' là ảnh của N qua phép đối xứng trục 
 là đường trung trực của đoạn thằng NN' nên trung điềm của đoạn thẳng NN' thuộc
là đường trung trực của đoạn thằng NN' nên trung điềm của đoạn thẳng NN' thuộc  và đường thẳng NN' vuông góc với
và đường thẳng NN' vuông góc với  .
. Đường thằng NN' đi qua N (-1; 2) và nhận vectơ pháp tuyến 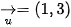 của
của 
Do đó
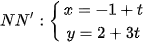
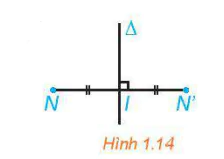
Giả sử toạ độ của N' là (–1+t; 2+3t).
Đoạn thẳng NN có trung điểm 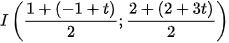 thuộc
thuộc  nên
nên
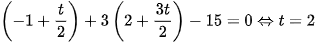
Vậy điểm N(-1; 2) có ành qua phép đối xứng trục  là N'(1; 8).
là N'(1; 8).
| >Luyện tập 1. Xét mặt phằng toạ độ Oxy (H. 1.15). Trong các khẳng định sau, chọn các khẳng định đúng. a) Phép đối xứng trục Ox biến mỗi điểm M(x; y) thành điểm có toạ độ (x;- у). b) Phép đối xứng trục Oy biến mỗi điểm M(x; y) thành điểm có toạ độ (-x; у). c) Phép đối xứng trục Ox biến A(1; 2) thành điềm A'(-1; -2). | 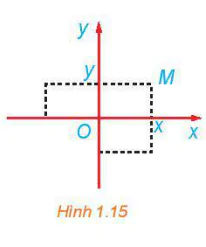 |
(Trang 14)
2. TÍNH CHẤT
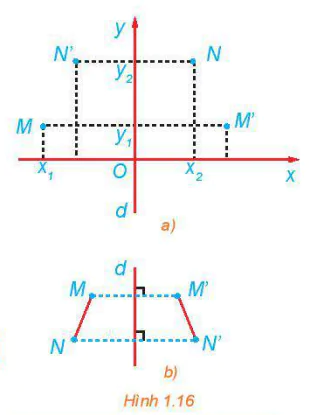
| >HĐ 2. Cho phép đối xứng trục ở biển M thành M', N thành N'. Xét hệ trục toạ độ Oxy sao cho trục Oy trùng với d (H.1.16a). Giả sử M có toạ độ là (x1; y1), N có toạ độ là (x2; y2). a) Hãy cho biết toạ độ của M', N'. b) Tính MN2, M'N'2 theo toạ độ của các điểm tương ứng. c) So sánh độ dài các đoạn thẳng MN, M'N'.
|  |
Từ tính chất trên, ta có thể rút ra:
| Phép đối xứng trục biến:
|
>Ví dụ 2. Trong mặt phẳng toạ độ Oxy, cho đường tròn
(C): x2 + y2 - 6x - 10y - 2=0.
Viết phương trình đường tròn (C') là ảnh của (C) qua phép đối xứng trục 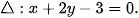
Giải
Ta có (C): (x - 3)2+(y - 5)2 = 62, nên (C) có tâm A(3; 5) và bán kính R = 6. Đường tròn ảnh (C') có bán kính R'= R = 6 và có tâm A' đối xứng với A qua A. Tương tự Vi dụ 1, ta tính được toạ độ của A' là (- 1; -3). Vậy (C) có phương trình là (x + 1)2+ (y + 3)2 = 62.
>Luyện tập 2. Trong mặt phẳng toạ độ Oxy, cho đường thẳng d: 3x - y - 1= 0. Viết phương trình đường thắng d' là ảnh của đường thẳng d qua phép đối xứng trục Ox.
(Trang 15)
>Ví dụ 3. Cho đường thẳng  và hai điểm
và hai điểm  , B không thuộc đường thẳng đó. Tìm điểm M thuộc
, B không thuộc đường thẳng đó. Tìm điểm M thuộc  đề MA + MB nhỏ nhất.
đề MA + MB nhỏ nhất.
| Giải Trường hợp 1. A và B thuộc hai nửa mặt phẳng bờ Ta có MA+ MB ≥ AB, dấu đẳng thức xảy ra khi và chỉ khi M thuộc đoạn thẳng AB. Mặt khác M thuộc Trường hợp 2. A và B thuộc cùng nửa mặt phẳng bờ  và đoạn thẳng A'B. Do đó, MA + MB nhỏ nhất bằng A'B, khi M là giao điểm của và đoạn thẳng A'B. Do đó, MA + MB nhỏ nhất bằng A'B, khi M là giao điểm của  và đoạn thắng A'B. và đoạn thắng A'B. | 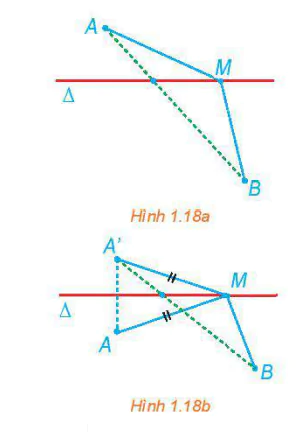 |
>Luyện tập 3. Cho đường thẳng  và hai điểm A, B, sao cho
và hai điểm A, B, sao cho 
 (M không thuộc đường thẳng AB). Gọi M’ là điểm sao cho A, B, M, M' là 4 đỉnh của một hình thang cân nhận AB là một cạnh đáy. Chứng minh rằng M' thay đổi trên một đường thằng cố định.
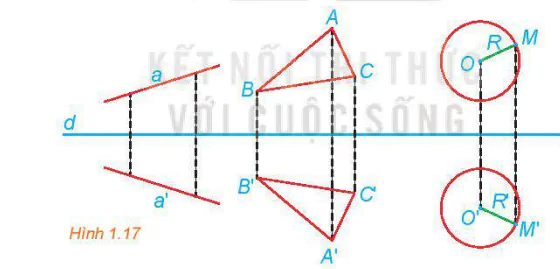
(M không thuộc đường thẳng AB). Gọi M’ là điểm sao cho A, B, M, M' là 4 đỉnh của một hình thang cân nhận AB là một cạnh đáy. Chứng minh rằng M' thay đổi trên một đường thằng cố định. | >Vận dụng. Bằng quan sát, hãy cho biết, trong hai hình ảnh bên, hình nào có trục đối xứng. |  |  |
BÀI TẬP
1.6. Cho hai điểm phân biệt A và B. Xác định phép đối xứng trục biến điểm A thành điểm B.
1.7. Cho hai đường tròn không đồng tâm, nhưng có cùng bán kính (O1; R) và (O2; R). Xác định phép đối xứng trục biến (O1; R) thành (O2; R).
1.8. Cho đường thẳng d và hai điểm phân biệt A, B sao cho đường thẳng AB không vuông góc với d. Gọi M, N tương ứng là các điểm đối xứng với A, B qua d. Hỏi A, B, M, N có là 4 đỉnh của một hình thang cân hay không?
1.9. Trong mặt phẳng toạ độ Oxy, cho 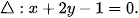 . Viết phương trình đường thẳng ở đối xứng với
. Viết phương trình đường thẳng ở đối xứng với 
1.10. Dùng com-pa, thước kẻ, bút, hãy vẽ lại các nét thẳng và tròn trong Hình 1.19.
Hình 1.19


 (H.1.18a). Khi đó đoạn thẳng AB và đường thẳng
(H.1.18a). Khi đó đoạn thẳng AB và đường thẳng 








































































Bình Luận
Để Lại Bình Luận Của Bạn