Nội Dung Chính
(Trang 26)
| THUẬT NGỮ
| KIẾN THỨC, KĨ NĂNG
|
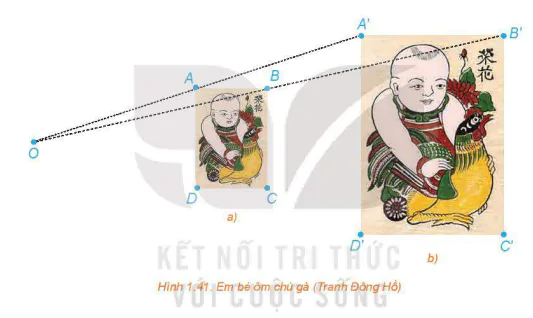
Hai bức tranh ở Hình 1.41 có hình dạng giống nhau nhưng khác nhau về kích thước, nên không có phép dời hình biến bức tranh này thành bức tranh kia. Tuy vậy, ta sẽ biết bức tranh này như là ảnh của bức tranh kia qua một phép vị tự – đối tượng mà ta sẽ học trong bài này.
1. PHÉP VỊ TỰ
>HĐ1. Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A′B′C′D′ có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ.
a) Giải thích vì sao các đường thẳng AA′, BB′, CC′, DD′ cùng đi qua một điểm O.
b) Hãy tính các tỉ số 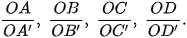
c) Dùng thước thẳng nối hai điểm tương ứng nào đó trên hai bức tranh (chẳng hạn, đầu mỏ trên của chú gà ở hai bức tranh). Đường thẳng đó có đi qua O hay không?
(Trang 27)
Cho điểm O và số thực k ≠ 0. Phép biến hình biến mỗi điểm M thành điểm M' sao cho 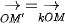 được gọi là phép vị tự tâm O, tỉ số k, kí hiệu là V(o.к) Điểm O gọi là tâm vị tự, k gọi là tỉ số vị tự. được gọi là phép vị tự tâm O, tỉ số k, kí hiệu là V(o.к) Điểm O gọi là tâm vị tự, k gọi là tỉ số vị tự. | 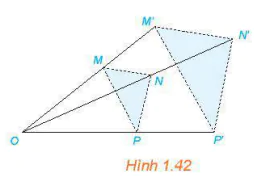 |
? Phép vị tự V(O, k) biến điểm O thành điểm nào? Nếu phép vị tự V(O, k) biến điểm M thành điểm M' thì phép vị tự 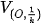 biến điềm M' thành điểm nào?
biến điềm M' thành điểm nào?
>Ví dụ 1. Cho tam giác ABC có ba đường trung tuyến AM, BN, CP và trọng tâm G.
a) Tìm ành của các điểm A, N, P qua phép vị tự V(A,2)
b) Tìm ảnh của các điểm A, B, C qua phép vị tự 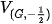
Giải
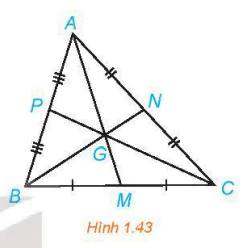
a) Phép vị tự V(A,2) biến điểm A thành điểm A. Do 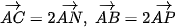 nên phép vị tự V(A,2) biến các điểm N, P tương ứng thành các điểm C, B.
nên phép vị tự V(A,2) biến các điểm N, P tương ứng thành các điểm C, B.
Vậy ảnh của các điểm A, N, P qua phép vị tự V(A,2) tương ứng là A, C, В.
b) VI G là trọng tâm của tam giác ABC nên 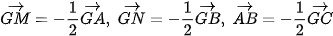 . Do đó. ảnh của các điểm A, B, C qua phép vị tự
. Do đó. ảnh của các điểm A, B, C qua phép vị tự 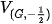 tương ứng là M, N, P.
tương ứng là M, N, P.
>Luyện tập 1. Chứng minh rằng, phép vị tự V(O, 1) là phép đồng nhất, phép vị tự V(O, -1) là phép đối xứng tâm O.
>Vận dụng 1. Quan sát hai bức tranh chú bé ôm gà ở phần mở đầu bài học và chỉ ra phép vị tự biến bức tranh nhỏ thành bức tranh lớn và phép vị tự biến bức tranh lớn thành bức tranh nhỏ.
2. TÍNH CHẤT
| >HĐ2. Cho phép vị tự tâm O, tỉ số k biến điểm M thành điểm M', điểm N thành điểm N'. a) Biểu diễn các vectơ  . . b) Giải thích vì sao | 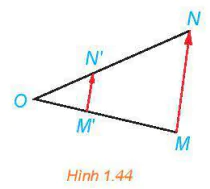 |
Nếu một phép vị tự tâm O, tỉ số k biến điềm M thành điểm M', điểm N thành điểm N thì 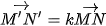 (và do đó, (và do đó, 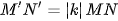 |
(Trang 28)
Chú ý. Từ tính chất trên, người ta chứng minh được rằng, phép vị tự tâm O, tỉ số k.
- Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa ba điểm đó;
- Biến đoạn thẳng (độ dài a) thành đoạn thằng (độ dài
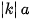 );
); - Biến đường tròn (bán kính R) thành đường tròn (bán kính
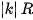 ) với tâm là ảnh của tâm;
) với tâm là ảnh của tâm; - Biến tam giác thành tam giác đồng dạng với nó (tỈ số đồng dạng là
 ):
): - Biến đường thẳng thành đường thằng song song hoặc trùng với đường thằng đó.
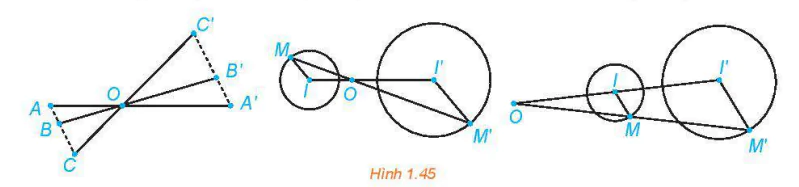
>Ví dụ 2. Một phép vị tự tâm O, tỉ số k biến tam giác ABC thành tam giác A'B'C'. Tính tỉ số diện tích hai tam giác A'B'C' và ABC.
Giải
Phép vị tự tỉ số k biến tam giác ABC thành tam giác A'B'C' nên tam giác A'B'C' đồng dạng với tam giác ABC theo ti số |k| (để ý rằng B'C'=|k|BC, C'A'=|K|CA, A'B'=|k|AB). Do đó, 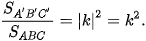
>Luyện tập 2. Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x -1)2 +(y -2)2 = 25.
a) Tìm tâm I và bán kính R của đường tròn (C).
b) Tìm tâm I' và bán kính R' của đường tròn (C') là ảnh của đường tròn (C) qua phép vị tự tâm A(3; 5), tỉ số 2.
c) Viết phương trình của (C').

Tâm I'(x; y) của (C') thoả mãn 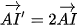
>Ví dụ 3. Cho đường tròn (O, R) và hai điềm phân biệt B, C sao cho đường thẳng BC và (O, R) không có điểm chung. Cho điểm A thay đổi trên đường tròn (O, R). Chứng minh rằng trọng tâm G của tam giác ABC thuộc một đường tròn cố định.
| Giải (H.1.46) Gọi M là trung điểm của đoạn thẳng BC. Vì G là trọng tâm tam giác ABC nên 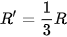 và O' là ảnh của O qua và O' là ảnh của O qua 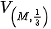 , nên được xác định bởi , nên được xác định bởi 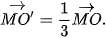 . . | 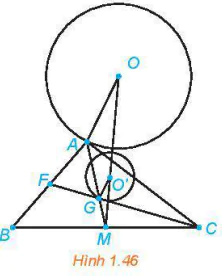 |
(Trang 29)
| >Vận dụng 2. Quan sát Hình 1.47 và cho biết hình nào trong hai hình nhỏ không phải là ảnh của hình lớn qua một phép vị tự. Nêu lí do cho sự lựa chọn đó. |
Hình 1.47 |
 |
BÀI TẬP
1.20. Cho hình thang ABCD có hai đáy AB và CD, CD = 2AB. Gọi O là giao của hai cạnh bên và I là giao của hai đường chéo. Tìm ảnh của đoạn thẳng AB qua các phép vị tự V(O, 2), V(I, -2)
1.21. Trong mặt phẳng toạ độ Oxy, cho A(1; 2), B(3; 6). Viết phương trình đường tròn (C) là ảnh của đường tròn đường kính AB qua phép vị tự V(O, 3).
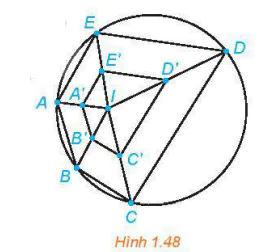
1.22. Ở Hình 1.48, A', B', C', D', E' tương ứng là trung điểm của các đoạn thẳng IA, IB, IC, ID, IE. Hỏi năm điểm đó có thuộc một đường tròn hay không? Vì sao?
1.23. Quan sát ba hình được tô màu ở Hình 1.49, hình nhỏ nào là ảnh của hình lớn qua một phép vị tự?
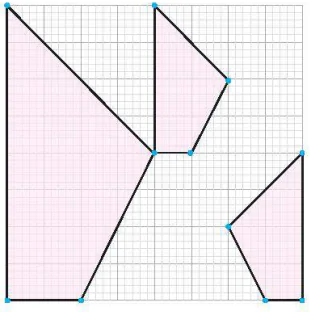
Hình 1.49
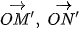
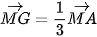 . Do đó, phép vị tự tâm M, tỉ số
. Do đó, phép vị tự tâm M, tỉ số 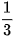 biến điểm A thành điểm G. Mặt khác, A thuộc đường tròn 3 (O, R) nên G thuộc đường tròn (O', R') cố định là ảnh của đường tròn (O, R) qua phép vị tự
biến điểm A thành điểm G. Mặt khác, A thuộc đường tròn 3 (O, R) nên G thuộc đường tròn (O', R') cố định là ảnh của đường tròn (O, R) qua phép vị tự 








































































Bình Luận
Để Lại Bình Luận Của Bạn