Nội Dung Chính
(Trang 19)
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| Tích hai đa thức
|
|
Giả sử độ dài hai cạnh của một hình chữ nhật được biểu thị bởi 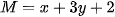
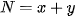 . Khi đó, diện tích của hình chữ nhật được biểu thị bởi
. Khi đó, diện tích của hình chữ nhật được biểu thị bởi 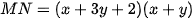
Trong tình huống này, ta phải nhân hai đa thức M và N. Phép nhân đó được thực hiện như thế nào và kết quả có phải là một đa thức hay không?
Bài học này sẽ cho các em câu trả lời cho các câu hỏi đó.
1. NHÂN ĐƠN THỨC VỚI ĐA THỨC
 Nhân hai đơn thức
Nhân hai đơn thức
Để nhân hai đơn thức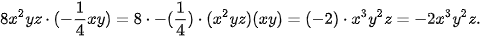
Qua ví dụ trên, ta có thể nói:
Muốn nhân hai đơn thức, ta nhân hai hệ số với nhau và nhân hai phần biến với nhau.
Ví dụ 1 Thực hiện phép nhân 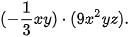
Giải
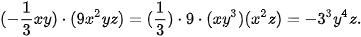
Luyện tập 1 Nhân hai đơn thức:
a) 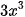 và
và 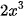 b)
b) 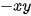 và
và 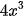
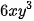 và
và 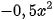 .
. (Trang 20)
 Nhân đơn thức với đa thức
Nhân đơn thức với đa thức
HĐ1: Hãy nhớ lại quy tắc nhân đơn thức với đa thức trong trường hợp chúng có một biến : bằng cách thực hiện phép nhân 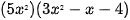 .
.
HĐ2: Bằng cách tương tự, hãy làm phép nhân 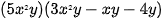
Ta rút ra quy tắc sau:

Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.
Ví dụ 2 Thực hiện phép nhân: 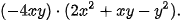
Giải 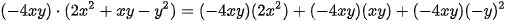
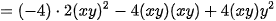
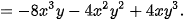
Luyện tập 2 Làm tính nhân:
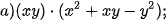
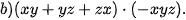
Vận dụng Rút gọn biểu thức: 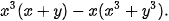
2 NHÂN ĐA THỨC VỚI ĐA THỨC
 Nhân hai đa thức
Nhân hai đa thức
HĐ3 Hãy nhớ lại quy tắc nhân hai đa thức một biến bằng cách thực hiện phép nhân:
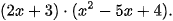
HĐ4 Bằng cách tương tự, hãy thử làm phép nhân 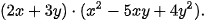
Ta rút ra quy tắc nhân hai đa thức như sau:
Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Chú ý
- Phép nhân đa thức cũng có tính chất tưởng tự phép nhân các số như:
A · B = B · A (giao hoán); (A · B) · C = A · (B · C) (kết hợp);
A · ( B · C) = A · B + A · C (phân phối đối với phép cộng).
- Nếu A, B, C là những đa thức tùy ý thì A · B · C = (A · B) · C = A · ( B · C).
(Trang 21)
Ví dụ 3

Trở lại tình huống mở đầu, ta thực hiện phép nhân như sau:
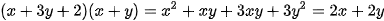
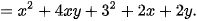
Ta thấy kết quả cũng là một đa thức.
Ví dụ 4 Rút gọn biểu thức 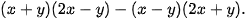
Giải
Biểu thức đã cho có dạng A-B, trong đó 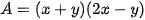 và
và 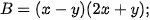
Từ đó ta có: 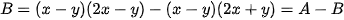
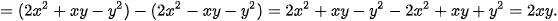
Luyện tập 3 Thực hiện phép nhân:
a) 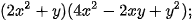 b)
b) 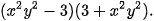
 Thử thách nhỏ
Thử thách nhỏ

Xét biểu thức đại số với hai biến k và m sau:
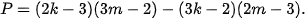
a) Rút gọn biểu thức P.
b) Chứng minh rằng tại mọi giá trị nguyên của k và m, giá trị của biểu thức P luôn là một số nguyên chia hết cho 5.
BÀI TẬP
1.24. Nhân hai đơn thức:
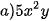 và
và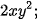 b)
b) 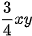 và
và 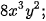
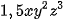 và
và 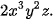
1.25. Tìm đơn thức với đa thức:
a) 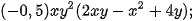 b)
b) 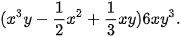
1.26. Rút gọn biểu thức: 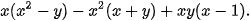
1.27. Làm tính nhân:
a) 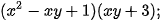 b)
b) 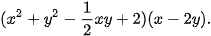
1.28. Rút gọn biểu thức sau để thấy rằng giá trị của nó không phụ thuộc vào giá trị của biến: 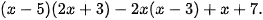
1.29. Chứng minh đẳng thức sau: 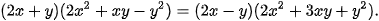






































Bình Luận
Để Lại Bình Luận Của Bạn