Nội Dung Chính
(Trang 62)
Ví dụ 1
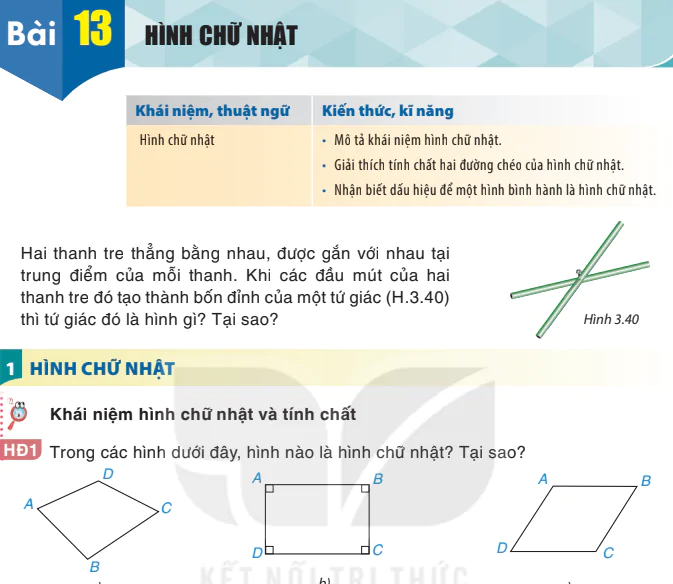
Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA của hình bình hành ABCD. Hỏi EFGH là hình gì? Vì sao?
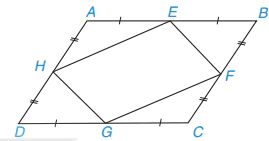
Hình 3.37
Giải (H.3.37)
Theo giả thiết, E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA của hình bình hành ABCD nên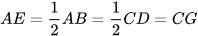 
; 
.
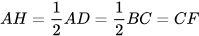Hai tam giác AHE và CFG có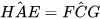 
(hai góc đối của hình bình hành ABCD),
AH=CF, AE=CG (chứng minh trên).
Vậy △AHE = △CFG (c.g.c), suy ra HE=FG. Tương tự, GH=EF
Tứ giác EGFH có GH=EF, HE=FG nên tứ giác đó là hình bình hành.
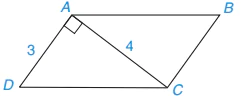
Ví dụ 2 Tính diện tích hình bình hành ABCD có đường chéo AC vuông góc với cạnh AD, biết AC = 4 cm, AD = 3 cm.
Hình 3.38
Giải (H.3.38)
Theo giả thiết, ABCD là hình bình hành nên BC II AD, BC = AD (= 3 cm). Mặt khác, AD ⊥ AC (giả thiết) suy ra BC ⊥ AC.
Ta có △ABC vuông tại C và △ADC vuông tại A nên:
) 
()
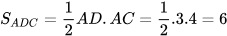
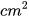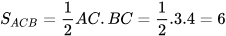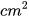Vậy diện tích hình bình hành ABCD là 12.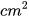
(Trang 63)
BÀI TẬP
3.19. Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao?
Hình 3.39
3.20. Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:
a) AN = CM; b)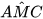 
= 
.
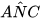3.21. Vẽ tứ giác ABCD theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB.
Bước 2. Lấy điểm C ∈ a.
Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC. Hãy giải thích tại sao tứ giác ABCD là hình bình hành.
3.22. Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm.
a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?
b) Tính khoảng cách từ giao điểm đó đến điểm C.
3.23. Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:
a) Hai tứ giác AEFD, ABFC là những hình bình hành;
b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.
3.24. Cho ba điểm không thẳng hàng.
a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành. Hãy vẽ hình và mô tả cách tìm.
b) Hỏi tìm được bao nhiêu điểm như vậy?
Bình Luận
Để Lại Bình Luận Của Bạn