Nội Dung Chính
(Trang 78)
Các em gặp rất nhiều hình ảnh trong cuộc sống và thế giới tự nhiên được tạo nên bởi các hình giống nhau. Chẳng hạn, những toà nhà trong thành phố, những bông hoa trên cây,... Những hình như vậy trong mặt phẳng ta gọi là hình đồng dạng. Trong chương này các em sẽ được tìm hiểu về chúng, đặc biệt là các tam giác đồng dạng.
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| - Hai tam giác đồng dạng - Tỉ số đồng dạng | - Nhận biết hai tam giác đồng dạng và giải thích các tính chất của chúng. - Giải thích định lí về trường hợp đồng dạng đặc biệt của hai tam giác. |
Có một chiếc bóng điện được mắc trên đỉnh (điểm A) của cột đèn thẳng đứng. Để tính chiều cao AB của cột đèn, bác Dương cắm một chiếc cọc gỗ (đoạn CD) thẳng đứng trên mặt đất rồi đo chiều dài bóng của cọc gỗ do ánh đèn điện tạo ra và đo khoảng cách từ điểm E đến chân cột đèn (điểm B) (H.9.1). Theo em, bác Dương đã tính như thế nào để ra được chiều cao cột đèn?
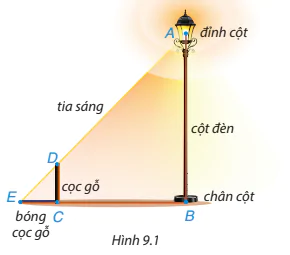
(Trang 79)
1 ĐỊNH NGHĨA
Chúng ta đã biết hai tam giác bằng nhau sẽ có các góc tương ứng bằng nhau và hình dạng giống nhau. Trong bài này chúng ta sẽ tìm hiểu một trường hợp mà hai tam giác có thể không bằng nhau những vẫn có các góc bằng nhau và hình dạng giống nhau.
Hai tam giác đồng dạng
HĐ1 Trong Hình 9.2, △ABC và △DEF là hai tam giác có các cạnh tương ứng song song và các góc tương ứng bằng nhau, tức là AB // DE, AC // DF, BC // EF và Â=D, B= Ê,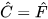 
.
Nhìn hình vẽ, hãy cho biết giá trị của các tỉ số sau:
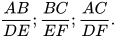
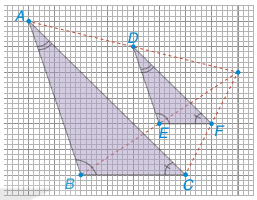
Hình 9.2
Hai tam giác như Hình 9.2 được gọi là hai tam giác đồng dạng. Cụ thể, ta có định nghĩa về hai tam giác đồng dạng như sau :
| Tam giác A'B'C' gọi là đồng dạng với tam giác ABC nếu:
Tam giác A'B'C' đồng dạng với tam giác ABC được kí hiệu là △A'B'C' ᔕ △ABC (viết theo thứ tự cặp đỉnh tương ứng). |  |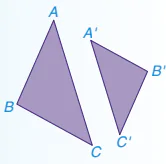
Tỉ số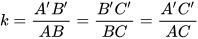 
được gọi là tỉ số đồng dạng của △A'B'C' với △ABC.
Nhận xét
• △A'B'C' ᔕ △ABC với tỉ số đồng dạng k thì △ABC ᔕ △A'B'C' với tỉ số đồng dạng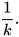 
Do vậy khi △A'B'C' ᔕ △ABC thì ta nói hai tam giác A'B'C' và ABC đồng dạng với nhau.
• Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng k = 1. Đặc biệt mọi tam giác đồng dạng với chính nó.
• Nếu △A"B"C" ᔕ △A'B'C' với tỉ số đồng dạng k và △A'B'C' ᔕ △ABC với tỉ số đồng dạng m thì △A"B"C" ᔕ △ABC với tỉ số đồng dạng k . m.
(Trang 80)
Ví dụ 1
Cho ABC và A'B'C' là hai tam giác đều có AB = 4 cm, A'B' = 3 cm. Chứng minh rằng △A'B'C' ᔕ △ABC và tìm tỉ số đồng dạng.
Giải
Ta có: BC = CA= AB= 4 cm, BC = C'A'= A'B' = 3 cm,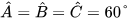 
và 
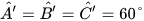
Do vậy hai tam giác ABC và A'B'C' có: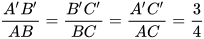 
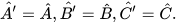
Vậy △A'B'C' ᔕ △ABC với tỉ số đồng dạng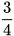 
.
Luyện tập 1
Trong các tam giác được vẽ trên ô lưới vuông (H.9.3), có một cặp tam giác đồng dạng. Hãy chỉ ra cặp tam giác đó, viết đúng kí hiệu đồng dạng và tìm tỉ số đồng dạng của chúng.
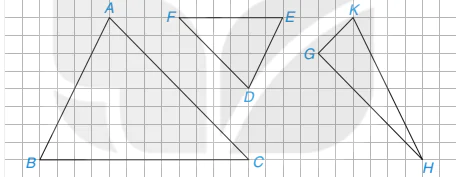
Hình 9.3
Thử thách nhỏ
Cho △ABC ᔕ △MNP. Chứng minh rằng:
a) Nếu tam giác ABC cân tại đỉnh A thì tam giác MNP cân tại đỉnh M.
b) Nếu tam giác ABC đều thì tam giác MNP đều.
c) Nếu AB ≥ AC ≥ BC thì MN ≥ MP ≥ NP.
2 ĐỊNH LÍ
Tìm hiểu định lí
HĐ2 Cho tam giác ABC và các điểm M, N lần lượt nằm trên các cạnh AB, AC sao cho MN song song với BC như Hình 9.4.
– Hãy viết các cặp góc bằng nhau của hai tam giác ABC và AMN, giải thích vì sao chúng bằng nhau.
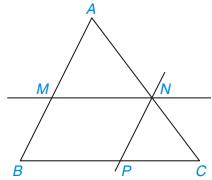
Hình 9.4
(Trang 81)
– Kẻ đường thẳng đi qua N song song với AB và cắt BC tại P. Hãy chứng tỏ MN=BP và suy ra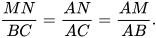 
– Tam giác ABC và tam giác AMN có đồng dạng không? Nếu có hãy viết đúng kí hiệu đồng dạng.
Tổng quát, ta có định lí sau:
| Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho. |
| GT | △ABC, MN // BC (M ∈ AB; N ∈ AC). |
| KL | △AMN ᔕ △ABC. |
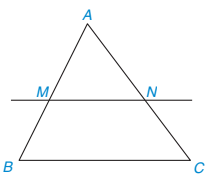
Hình 9.5
Chú ý. Định lí trên vẫn đúng nếu thay bằng đường thẳng cắt phần kéo dài của hai cạnh tam giác. Chẳng hạn, trong Hình 9.6 có ED // BC. Khi đó, △ADE ᔕ △ABC.
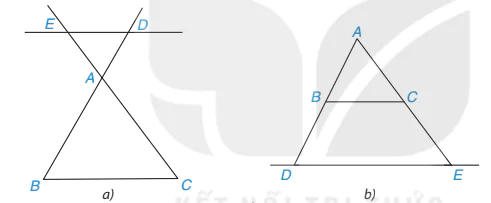
Hình 9.6
Ví dụ 2
Cho Hình 9.7, trong đó M, N lần lượt là trung điểm của AB, AC; P, Q lần lượt là trung điểm của AM, AN. Hãy liệt kê tất cả các cặp tam giác (phân biệt) đồng dạng.
Giải
Tam giác ABC có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác ABC. Suy ra MN // BC. (1)
Do đó △AMN ᔕ △ABC (theo định lí trên).
Tương tự, PQ là đường trung bình của tam giác AMN nên PQ // MN. (2)
Do đó △APQ ᔕ △AMN (theo định lí trên).
Từ (1) và (2), suy ra PQ // BC. Do đó △APQ ᔕ △ABC (theo định lí trên).
Vậy có tất cả ba cặp tam giác đồng dạng là: △AMN ᔕ △ABC; △APQ ᔕ △AMN và △ΑΡQ ᔕ △ΑΒC.
(Trang 82)
Luyện tập 2
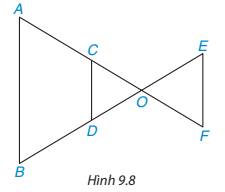
Trong Hình 9.8, các đường thẳng AB, CD, EF song song với nhau. Hãy liệt kê ba cặp tam giác (phân biệt) đồng dạng.
Vận dụng
Trở lại tình huống mở đầu, hãy giải thích bác Dương đã tính được chiều cao cột đèn như thế nào, biết cọc gỗ cao 1 m, EC = 80 cm và EB = 4 m.
BÀI TẬP
9.1. Cho AABC có AMNP, khẳng định nào sau đây không đúng?
a) △MNP ᔕ △ABC.
b) △BCA ᔕ △NPM.
c) △CAB ᔕ △PMN.
d) △ACB ᔕ △MNP.
9.2. Khẳng định nào sau đây là đúng?
a) Hai tam giác bằng nhau thì đồng dạng với nhau.
b) Hai tam giác bất kì đồng dạng với nhau.
c) Hai tam giác đều bất kì đồng dạng với nhau.
d) Hai tam giác vuông bất kì đồng dạng với nhau.
e) Hai tam giác đồng dạng thì bằng nhau.
9.3. Trong Hình 9.9, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng.
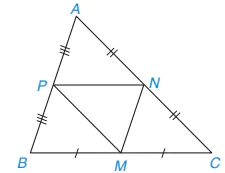
Hình 9.9
9.4. Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng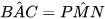 
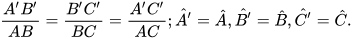
Các Bài Học Khác
Bình Luận
Để Lại Bình Luận Của Bạn