Nội Dung Chính
(Trang 98)
| Kiến thức, kĩ năng • Giải thích các trường hợp đồng dạng của tam giác vuông. • Giải quyết một số vấn đề thực tiễn gắn với việc vận dụng các tam giác vuông đồng dạng. |
Nam và Việt muốn đo chiều cao của cột cờ ở sân trường mà hai bạn không trèo lên được. Vào buổi chiều, Nam đo thấy bóng của cột cờ dài 6 m và bóng của Việt dài 70 cm. Nam hỏi Việt cao bao nhiêu, Việt trả lời là cao 1,4 m. Nam liền reo lên: “Tớ biết cột cờ cao bao nhiêu rồi đấy!”. Vậy cột cờ cao bao nhiêu và làm sao bạn Nam biết được?
Qua bài này, các em sẽ có câu trả lời cho câu hỏi trên.
1 ÁP DỤNG CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC VÀO TAM GIÁC VUÔNG
Từ các trường hợp đồng dạng góc – góc và cạnh – góc – cạnh của hai tam giác trong bài trước, ta suy ra hai định lí sau:
Định lí 1. Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Định lí 2. Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
|
Hình 9.47 | △ABC vuông tại A, △A'B'C' vuông tại A.
|
Hãy chỉ ra hai cặp tam giác vuông đồng dạng trong Hình 9.48.
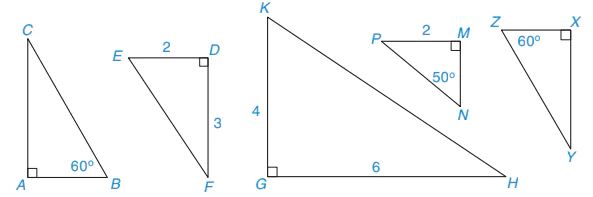
Hình 9.48
(Trang 99)
Ví dụ 1
Cho tam giác ABC có các đường cao AD, BE, CF cắt nhau tại điểm H.
Chứng minh rằng:
a) HA.HD=HB.HE=HC.HF;
b) △AEF ᔕ △ABC.
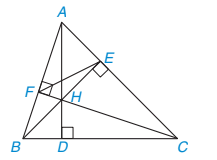
Hình 9.49
Giải. (H.9.49)
| GT | △ABC, các đường cao AD, BE, CF đồng quy tại H. |
| KL | HA.HD=HB.HE=HC.HF; △AEF ᔕ △ABC. |
a) Hai tam giác vuông AHF (vuông tại F) và CHD (vuông tại D) có:
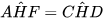 (hai góc đối đỉnh).
(hai góc đối đỉnh).
Do đó △AEF ᔕ △CHD. Suy ra 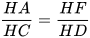 , hay HA.HD=HC.HF. (1)
, hay HA.HD=HC.HF. (1)
Tương tự, 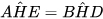 (hai góc đối đỉnh) nên hai tam giác vuông AHE (vuông tại E) và BHD (vuông tai D) đồng dạng với nhau.
(hai góc đối đỉnh) nên hai tam giác vuông AHE (vuông tại E) và BHD (vuông tai D) đồng dạng với nhau.
Suy ra 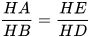 hay HA.HD=HB.HE. (2)
hay HA.HD=HB.HE. (2)
Từ (1) và (2) suy ra HA.HD=HB.HE=HC.HF.
b) Hai tam giác ABE (vuông tại E) và ACF (vuông tại F) có góc  chung nên △ABE ᔕ △ACF. Suy ra 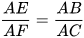
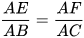 .
. Hai tam giác AEF và ABC có: Â chung, 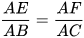 (chứng minh trên).
(chứng minh trên).
Vậy △AEF ᔕ △ABC (c.g.c).
Luyện tập 1
Trở lại tình huống mở đầu, ta thấy chiếc cột cùng với bóng của nó tạo thành hai cạnh góc vuông của tam giác ABC vuông tại đỉnh A, bạn Việt và bóng của mình cũng được xem là hai cạnh góc vuông của tam giác A'B'C vuông tại đỉnh A' (H.9.50). Vì các tia sáng Mặt Trời tạo với hai cái bóng các góc bằng nhau nên 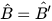 .
.
a) Hai tam giác vuông ABC và A'B'C' có đồng dạng với nhau không?
b) Bạn Nam đã tính chiều cao chiếc cột, tức là độ dài đoạn thẳng AB như thế nào và kết quả là bao nhiêu?
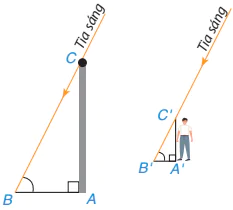
Hình 9.50
(Trang 100)
Thử thách nhỏ
Một người đo chiều cao của một cái cây bằng cách chôn một chiếc cọc xuống đất, cọc cao 2,4 m và cách vị trí gốc cây 19 m. Người đó đứng cách xa chiếc cọc 1 m và nhìn thấy đỉnh cọc thẳng với đỉnh của cây. Hãy tính chiều cao của cây, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6 m (H.9.51).
A: vị trí đỉnh cây
B: vị trí gốc cây
C: vị trí đỉnh cột
M: vị trí mắt
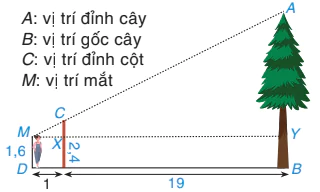
Hình 9.51
2 TRƯỜNG HỢP ĐỒNG DẠNG ĐẶC BIỆT CỦA HAI TAM GIÁC VUÔNG
HĐ1 Các tam giác vuông AHB và A'H'B' trong Hình 9.52 mô tả hai con dốc có chiều dài lần lượt là AB = 13 m, A'B' = 7,5 m và độ cao lần lượt là BH = 5 m, B'H' = 2,5 m. Độ dốc của hai con dốc lần lượt được tính bởi số đo góc HAB và H'A'B'.

Hình 9.52
– Nhận xét về hai đại lượng 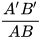 và
và 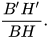
– Dùng định lí Pythagore để tính AH và A'H'.
– So sánh các đại lượng 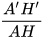 và
và 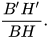
– Hai tam giác vuông A'H'B' và AHB có đồng dạng không? Từ đó rút ra kết luận gì về độ dốc của hai con dốc.
Tổng quát, ta có định lí sau:
Định lí (trường hợp đồng dạng đặc biệt của hai tam giác vuông)
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
(Trang 101)
Chứng minh định lí (H.9.53)
| GT | △ABC, △A'B'C', Â=90°, 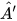 =90°, =90°, 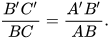 |
| KL | △A'B'C' ᔕ △ABC. |
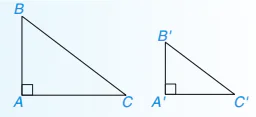
Hình 9.53
Áp dụng định lí Pythagore cho các tam giác vuông A'B'C' và ABC, ta được:
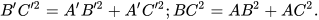
Suy ra 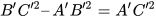
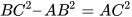 . Vậy từ giả thiết
. Vậy từ giả thiết 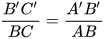 , ta có:
, ta có: 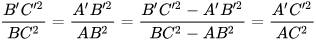 .
. Do đó, 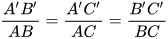 . Suy ra △A'B'C' ᔕ △ABC (c.c.c)
. Suy ra △A'B'C' ᔕ △ABC (c.c.c)
Hãy chỉ ra các cặp tam giác vuông đồng dạng với nhau trong Hình 9.54, viết đúng kí hiệu đồng dạng.
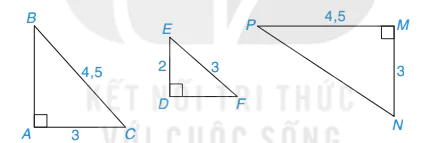
Hình 9.54
Giả sử các chân đường cao H, H' lần lượt hạ từ đỉnh A và A' của hai tam giác ABC và A'B'C' nằm trên các cạnh BC, B'C' thoả mãn 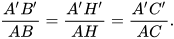 Chứng minh rằng △A'B'C' ᔕ △ABC.
Chứng minh rằng △A'B'C' ᔕ △ABC.
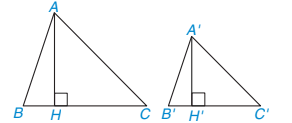
Hình 9.55
Giải. (H.9.55)
| GT | △A'B'C', △ABC, H thuộc cạnh BC, H' thuộc cạnh B'C', AH ⊥ BC, A'H' ⊥ B'C', 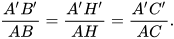 |
| KL | △A'B'C' ᔕ △ABC. |
(Trang 102)
Tam giác vuông ABH (vuông tại H) và tam giác vuông A'B'H' (vuông tạu H') có:
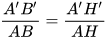 . Vậy △A'B'H' ᔕ △ABH. Suy ra
. Vậy △A'B'H' ᔕ △ABH. Suy ra 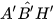
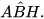 (1)
(1) Tam giác vuông ACH (vuông tại H) và tam giác vuông A'C'H' (vuông tại H') có:
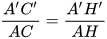 . Vậy △A'C'H' ᔕ △ACH. Suy ra
. Vậy △A'C'H' ᔕ △ACH. Suy ra 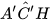 =
= 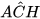 . (2)
. (2)
Hai tam giác ABC và A'B'C' có:
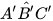
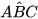 (theo (1)),
(theo (1)), 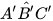 =
=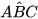 (theo (2)).
(theo (2)). Vậy △A'B'C' ᔕ △ABC (g.g).
Nhận xét. Ngược lại, nếu △A'B'C' ᔕ △ABC theo tỉ số k và AH, A'H' lần lượt là các đường cao của △ABC và △A'B'C' thì △A'B'H' có △ABH (do 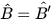 ) theo tỉ số k và
) theo tỉ số k và 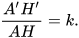
Luyện tập 2
Một ngôi nhà với hai mái lệch AB, CD được thiết kế như Hình 9.56 sao cho CD = 6 m, AB = 4 m, HA = 2 m, AC = 1 m. Chứng tỏ rằng 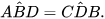
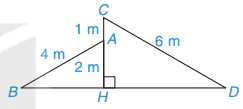
Hình 9.56
Vận dụng
Thường ngày đến công trường, bác Hoan dùng một chiếc thang lớn dựng lên một bức tường cao 6 m. Khi đặt chân thang cách chân tường 1,5 m thì vừa dựng thang lên đúng mặt trên bức tượng. "Hôm nay, bác Hoan chỉ có một chiếc thang nhỏ dài bằng 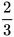 chiếc thang lớn. Để đảm bảo an toàn, bác đặt chân thang cách chân tường 1 m (H.9.57). Hỏi khi dựng chiếc thang nhỏ lên thì điểm cao nhất của thang cách mặt trên bức tường bao nhiêu mét?
chiếc thang lớn. Để đảm bảo an toàn, bác đặt chân thang cách chân tường 1 m (H.9.57). Hỏi khi dựng chiếc thang nhỏ lên thì điểm cao nhất của thang cách mặt trên bức tường bao nhiêu mét?
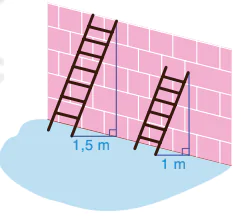
Hình 9.57
BÀI TẬP
9.23. Điều kiện nào dưới đây chứng tỏ rằng hai tam giác vuông đồng dạng?
a) Một góc nhọn của tam giác này bằng một góc nhọn của tam giác kia.
b) Cạnh góc vuông và cạnh huyền của tam giác này tỉ lệ với cạnh góc vuông và cạnh huyền của tam giác kia.
c) Một cạnh góc vuông của tam giác này bằng một cạnh góc vuông của tam giác kia.
d) Hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia.
(Trang 103)
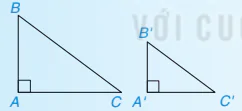
9.24. Cặp tam giác vuông nào đồng dạng với nhau trong Hình 9.58?
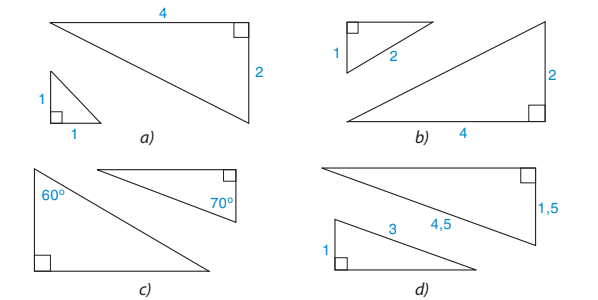
Hình 9.58
9.25. Cho góc nhọn xOy, các điểm A, N nằm trên tia Ox, các điểm B, M nằm trên tia Oy sao cho AM, BN lần lượt vuông góc với Oy, Ox. Chứng minh rằng tam giác OAM đồng dạng với tam giác OBN.
9.26. Cho hai hình chữ nhật ABCD và A'B'C'D' thoả mãn AC = 3AB, B'D' = 3A'B'.
a) Chứng minh rằng tam giác ABC đồng dạng với tam giác A'B'C'.
b) Nếu A'B' = 2AB và diện tích hình chữ nhật ABCD là 2 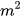 thì diện tích hình chữ nhật A'B'C'D' là bao nhiêu?
thì diện tích hình chữ nhật A'B'C'D' là bao nhiêu?
9.27. Cho tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k. Gọi A'H' và AH lần lượt là các đường cao đỉnh A' và A của tam giác A'B'C' và tam giác ABC. Chứng minh rằng:
a) 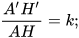
b) Diện tích tam giác A'B'C' bằng 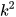 lần diện tích tam giác ABC.
lần diện tích tam giác ABC.
9.28. Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho AM = 2 m, AM vuông góc với AB và đo được số đo góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A'M'B' vuông tại A, có A'M' =1cm, 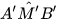 =
= 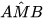

Hình 9.59
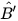 =
= 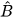 thì △A'B'C' ᔕ △ABC.
thì △A'B'C' ᔕ △ABC.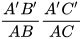 thì △A'B'C' ᔕ △ABC.
thì △A'B'C' ᔕ △ABC.





































Bình Luận
Để Lại Bình Luận Của Bạn