Ứng dụng định lí Thalès, định lí Pythagore và tam giác đồng dạng để đo chiều cao, khoảng cách | Toán 8 - Tập 2 | Hoạt động thực hành trải nghiệm tập 2 - Lớp 8 - Kết Nối Tri Thức Với Cuộc Sống

(Trang 128)

HĐ1 Dùng định lí Thalès để đo chiều cao của ngọn cây (toà nhà, toà tháp)

Chuẩn bị:

– Cọc thẳng cắm được trên mặt đất hoặc dựng đứng được, thước ngắm thẳng gắn ở trên cọc có thể quay được, thước dây, thước kẻ.

– Giấy, bút, máy tính cầm tay.

– Địa điểm thực hiện: sân trường, nơi dã ngoại.

– Chia lớp thành các nhóm, mỗi nhóm từ 6 đến 8 học sinh.

Hướng dẫn (H.T.1):

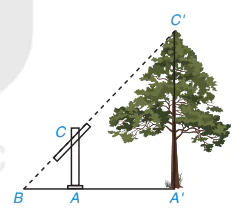
Hình T.1

– Dựng cọc AC thẳng đứng trên mặt đất, chỉnh cho thước ngắm đi qua đỉnh C' của ngọn cây.

– Xác định giao điểm B của đường thẳng đi qua CC' (chứa thước ngắm) với mặt đất.

– Gọi A' là gốc cây thì AC // A'C'. Theo định lí Thalès ta có: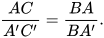

– Đo các khoảng cách AC, BA', BA và tính chiều cao A'C' của cây theo công thức: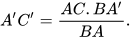

- Các nhóm cùng đo chiều cao của một cây nhưng ở các vị trí khác nhau và so sánh kết quả với nhau.

HĐ2 Dùng định lí Pythagore và tam giác đồng dạng để đo khoảng cách những điểm không tới được

Chuẩn bị:

– Giác kế ngang (dụng cụ đo góc trên mặt đất), thước dây.

– Giấy, bút, máy tính cầm tay.

– Địa điểm thực hiện: sân trường, dã ngoại.

– Chia lớp thành các nhóm, mỗi nhóm từ 6 đến 8 học sinh.

Hướng dẫn đo khoảng cách từ vị trí đang đứng (điểm A) đến vị trí khó đi đến được (điểm B) theo một trong hai phương pháp sau:

(Trang 129)

Phương pháp 1 (H.T.2):

– Dùng giác kế chọn một điểm C sao cho AC vuông góc AB, chọn điểm D trên đường thẳng BC sao cho AD vuông góc BC.

– Diện tích tam giác ABC bằng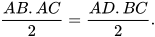

Do đó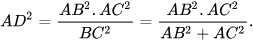

Suy ra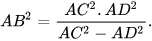

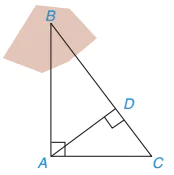
Hình T.2

– Đo độ dài các đoạn thẳng AC, AD và tính ra kết quả độ dài đoạn thẳng AB.

Phương pháp 2 (H.T.3):

– Lấy một điểm E tuỳ ý khác điểm A và không nằm trên đường thẳng AB.

– Sử dụng giác kế xác định số đo các góc 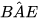và .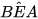

– Vẽ lên giấy tam giác A'B'E' có các góc A' và E' tương ứng bằng các góc A và E của tam giác ABE.

Như vậy tam giác A'B'E' đồng dạng với tam giác ABE. Suy ra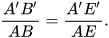

– Đo độ dài đoạn thẳng AE bằng thước dây và độ dài các đoạn thẳng A'B', A'E' bằng thước kẻ.

– Tính độ dài đoạn thẳng AB theo công thức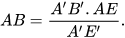

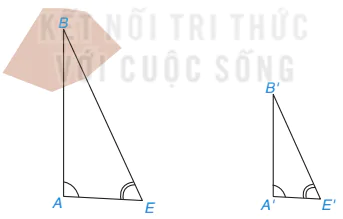
Hình T.3

Các nhóm khác nhau có thể xác định vị trí các điểm C, D, E khác nhau và so sánh kết quả cuối cùng với nhau.

Luyện tập

Trong Phương pháp 1 của HĐ2, chúng ta đã dùng định lí Pythagore để tính độ dài đoạn thẳng AB. Em hãy tính độ dài đoạn thẳng AB bằng một cách khác thông qua độ dài các đoạn thẳng AC, AD, CD.