Nội Dung Chính
(Trang 63)
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| Công thức tính xác suất | Tính xác suất bằng tỉ số giữa số kết quả thuận lợi cho biến cố và số kết quả có thể trong trường hợp các kết quả có thể là đồng khả năng. |
Một túi đựng 20 viên kẹo giống hệt nhau nhưng khác loại, trong đó có 7 viên kẹo sữa, 4 viên kẹo chanh, 6 viên kẹo dừa và 3 viên kẹo bạc hà. Bạn Lan lấy ngẫu nhiên một viên kẹo từ túi. Tính xác suất để Lan lấy được viên kẹo sữa.

| Các viên kẹo giống hệt nhau, chỉ khác loại nên có 4 kết quả có thể là lấy được viên kẹo sữa, viên kẹo chanh, viên kẹo dừa và viên kẹo bạc hà. Do đó, xác suất để Lan lấy được viên kẹo sữa là
| Không đúng, chỉ có 4 kết quả có thể nhưng chúng không đồng khả năng. Tớ thấy xác suất để Lan lấy được viên kẹo sữa là cao nhất vì trong túi có nhiều viên kẹo sữa nhất. Nhưng tớ không biết xác suất để Lan lấy được viên kẹo sữa chính xác là bao nhiêu?
|
Trong bài học này sẽ giúp các em trả lời được câu hỏi của bạn Tròn.
Cách tính xác suất bằng tỉ số
Muốn tính xác suất trong những tình huống tương tự như trên ta có công thức tính xác suất sau:
| Giả thiết rằng các kết quả có thể của một hành động hay thực nghiệm là đồng khả năng. Khi đó, xác suất của biến cố E, kí hiệu là P(E), bằng tỉ số giữa số kết quả thuận lợi cho biến cố E và tổng số kết quả có thể.
|
(Trang 64)
| Nhận xét. Việc tính xác suất của một biến cố E trong một hành động hay thực nghiệm đồng khả năng sẽ gồm các bước sau: Bước 1. Đếm các kết quả có thể (thường bằng cách liệt kê); Bước 2. Chỉ ra các kết quả có thể là đồng khả năng; Bước 3. Đếm các kết quả thuận lợi cho biến cố E; Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E và tổng số kết quả có thể. |
Ví dụ 1
Một tấm bìa cứng hình tròn được chia thành 12 hình quạt như nhau và đánh số 1; 2; 3;...; 12 (H.8.1), được gắn vào trục quay có mũi tên cố định ở tâm. Quay tấm bìa xem mũi tên chỉ vào hình quạt nào khi tấm bìa dừng lại, tính xác suất của các biến cố sau:
a) A: “Mũi tên chỉ vào hình quạt ghi số nguyên tố”;
b) B: “Mũi tên chỉ vào hình quạt ghi số chính phương”.
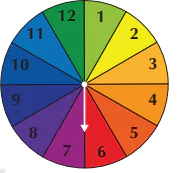
Hình 8.1
Giải
Có 12 kết quả có thể, đó là 1; 2;..; 12. Do 12 hình quạt như nhau nên 12 kết quả có thể này là đồng khả năng.
a) Các kết quả thuận lợi cho biến cố A là 2; 3; 5; 7; 11. Có 5 kết quả thuận lợi cho biến cố A. Do đó, xác suất của biến cố A là 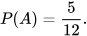
b) Các kết quả thuận lợi cho biến cố B là 1; 4; 9. Có 3 kết quả thuận lợi cho biến cố B. Do đó, xác suất của biến cố B là 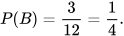
Luyện tập 1
Trở lại tình huống mở đầu. Tính xác suất để Lan lấy được:
a) Viên kẹo sữa;
b) Viên kẹo chanh.
Ví dụ 2
Một hộp đựng 18 viên bi cùng khối lượng và kích thước, với hai màu đỏ và vàng, trong đó số viên bi màu vàng gấp đôi số viên bi màu đỏ. Bình lấy ngẫu nhiên một viên bi từ trong hộp. Tính xác suất để Bình lấy được viên bi màu vàng.
(Trang 65)
Giải
Gọi x là số viên bi màu đỏ. Khi đó số viên bi màu vàng là 2x.
Theo đề bài, ta có x + 2x = 18, hay 3x = 18, tức là x = 6.
Do đó, số viên bi màu vàng là 12.
Do Bình lấy ngẫu nhiên một viên bi từ hộp có 18 viên nên có 18 kết quả có thể và các kết quả đó là đồng khả năng.
Vậy xác suất để Bình lấy được viên bi màu vàng là 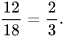
Luyện tập 2
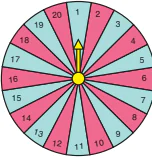
Trên giá sách của thư viện có 15 cuốn sách, trong đó có một số cuốn tiểu thuyết. Người thủ thư đặt thêm 5 cuốn tiểu thuyết thư viện mới mua vào giá sách. Bạn Nam đến mượn sách, chọn ngẫu nhiên một cuốn sách trên giá. Biết rằng xác suất để chọn được cuốn tiểu thuyết là 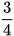 . Hỏi lúc đầu trên giá sách có bao nhiêu cuốn tiểu thuyết?
. Hỏi lúc đầu trên giá sách có bao nhiêu cuốn tiểu thuyết?
Tranh luận
Một túi đựng 17 viên bi cùng khối lượng và kích thước, chỉ khác màu, trong đó có 8 viên bi màu đỏ, 5 viên bi màu xanh và 4 viên bi màu vàng. Lấy ngẫu nhiên một viên bi từ trong túi. Tính xác suất của biến cố E: “Lấy được viên bi màu đỏ”.
| Có 17 viên bị nên có 17 kết quả có thể. Có 8 viên bị màu đỏ nên có 8 kết quả thuận lợi cho biến cố E. Vậy
| Các viên bi cùng khối lượng và kích thước, chỉ khác màu, nên chỉ có 3 kết quả có thể là viên bi màu đỏ, viên bi màu trắng và viên bi màu vàng. Do đó
|
Vuông và Tròn ai nói đúng? Tại sao?
BÀI TẬP
8.4. Một hình tròn được chia thành 20 hình quạt như nhau, đánh số từ 1; 2;...; 20 và được gắn vào trục quay có mũi tên cố định ở tâm (H.8.2). Quay tấm bìa và quan sát xem mũi tên chỉ vào hình quạt nào khi tấm bìa dừng lại.
Hình 8.2
(Trang 66)
Tính xác suất để mũi tên:
a) Chỉ vào hình quạt ghi số chia hết cho 4.
b) Chỉ vào hình quạt ghi số không phải là số nguyên tố.
8.5. Một túi đựng các viên kẹo giống hệt nhau, chỉ khác màu, trong đó có 5 viên kẹo màu đen, 3 viên kẹo màu đỏ, 7 viên kẹo màu trắng. Lấy ngẫu nhiên một viên kẹo trong túi.
Tính xác suất của các biến cố sau:
a) E: “Lấy được viên kẹo màu đen”;
b) F: “Lấy được viên kẹo màu đen hoặc màu đỏ”;
c) G: “Lấy được viên kẹo màu trắng”;
d) H: “Không lấy được viên kẹo màu đỏ”.
8.6. Trong một chiếc hộp có 15 tấm thẻ giống nhau được đánh số 10; 11;...; 24. Rút ngẫu nhiên một tấm thẻ từ trong hộp. Tính xác suất của các biến cố sau:
a) A: “Rút được tấm thẻ ghi số lẻ”;
b) B: “Rút được tấm thẻ ghi số nguyên tố”.
8.7. Trò chơi vòng quay may mắn.
Một bánh xe hình tròn được chia thành 12 hình quạt như nhau, trong đó có 2 hình quạt ghi 100 điểm, 2 hình quạt ghi 200 điểm, 2 hình quạt ghi 300 điểm, 2 hình quạt ghi 400 điểm, 1 hình quạt ghi 500 điểm, 2 hình quạt ghi 1.000 điểm, 1 hình quạt ghi 2.000 điểm (H.8.3). Ở mỗi lượt, người chơi quay bánh xe. Mũi tên cố định gắn trên vành bánh xe dừng ở hình quạt nào thì người chơi nhận được số điểm ghi trên hình quạt đó.
Bạn Lan chơi trò chơi này. Tính xác suất của các biến cố sau:
a) A: “Trong một lượt quay, Lan được 400 điểm”;
b) B: “Trong một lượt quay, Lan được ít nhất 500 điểm”.

Hình 8.3
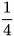


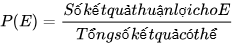
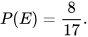

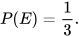





































Bình Luận
Để Lại Bình Luận Của Bạn