(Trang 40)
| Khái niệm, thuật ngữ | Kiến thức, kĩ năng |
| - Hàm số - Biến số - Mặt phẳng toạ độ - Toạ độ của điểm - Đồ thị của hàm số | - Nhận biết những mô hình thực tế dẫn đến khái niệm hàm số. - Tính giá trị của hàm số khi hàm số đó xác định bởi công thức. - Xác định toạ độ của một điểm trên mặt phẳng toạ độ; xác định một điểm trên mặt phẳng toạ độ khi biết toạ độ của nó. - Nhận biết đồ thị hàm số. |
Hình 7.1 là biểu đồ đoạn thẳng mô tả sản lượng tiêu thụ ô tô của thị trường Việt Nam trong 5 tháng đầu năm 2020. Em hãy cho biết trong tháng nào thì số lượng ô tô tiêu thụ là ít nhất.
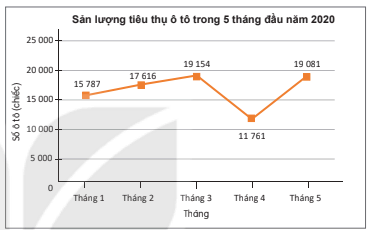
Hình 7.1. (Theo Hiệp hội các nhà sản xuất ô tô Việt Nam (VAMA))
1 KHÁI NIỆM HÀM SỐ
Nhận biết khái niệm hàm số
HĐ1 Quảng đường đi được 5 (km) của một ô tô chuyển động với vận tốc 60 km/h được cho bởi công thức S = 60t, trong đó t (giờ) là thời gian ô tô di chuyển.
a) Tính và lập bảng các giá trị tương ứng của S khi t nhận các giá trị lần lượt là 1; 2; 3; 4 (giờ).
b) Với mỗi giá trị của t, ta xác định được bao nhiêu giá trị tương ứng của S?
HĐ2 Nhiệt độ T (°C) tại các thời điểm t (giờ) của Hà Nội vào một ngày được cho trong bảng sau:
| t (giờ) | 0 | 4 | 8 | 12 | 16 | 20 |
| T (°C) | 24 | 25 | 27 | 30 | 28 | 27 |
a) Hãy cho biết nhiệt độ của Hà Nội vào thời điểm 12 giờ trưa ngày hôm đó.
b) Với mỗi giá trị của t, ta xác định được bao nhiêu giá trị tương ứng của T?
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biển số.
(Trang 41)
Chú ý. Khi y là hàm số của x, ta thường viết y = f(x), y = g(x),... Chẳng hạn, với hàm số y = 2x + 1, ta còn viết y = f(x) = 2x + 1. Khi đó, thay cho câu “Khi x bằng 1 thì giá trị tương ứng của y là 3”, ta viết ngắn gọn là f(1) = 3.
Ví dụ 1
Cho hàm số y = f(x) = 3x. Lập bảng các giá trị tương ứng của y khi x nhận các giá trị lần lượt là -2; -1; 0; 1; 2.
| Hàm số có thể được cho bằng công thức (như ở HĐ1), bằng bảng (như ở HĐ2),...
|
Giải
Bảng các giá trị tương ứng của y:
| x | -2 | -1 | 0 | 1 | 2 |
| y=f(x)=3x | -6 | -3 | 0 | 3 | 6 |
Ví dụ 2
Các giá trị tương ứng của hai đại lượng x và y được cho bởi các bảng sau. Đại lượng y có phải là một hàm số của đại lượng x không?
a)
| x | -3 | -2 | 2 | 4 | 6 |
| y | -4 | -6 | 6 | 3 | 2 |
b)
| x | -2 | -1 | 0 | 1 | -2 |
| y | -1 | 0 | 1 | 2 | 1 |
Giải
a) Đại lượng y là hàm số của x vì với mỗi giá trị của x (x ∈ {-3; -2; 2; 4; 6}), ta luôn xác định được chỉ một giá trị tương ứng của y.
b) Đại lượng y không phải là một hàm số của x vì với x = -2 ta xác định được hai giá trị tương của y ( y = -1 và y = 1).
Luyện tập 1
Viết công thức tính thời gian di chuyển t (giờ) của một ô tô chuyển động trên quãng đường dài 150 km với vận tốc không đổi v (km/h). Thời gian di chuyển t có phải là một hàm số của vận tốc v không? Tính giá trị của t khi v = 60 (km/h).
Vận dụng
Trở lại tình huống mở đầu, em hãy cho biết:
a) Tháng nào thì số lượng ô tô tiêu thụ là ít nhất và số tiêu thụ trong tháng đó là bao nhiêu?
b) Nếu gọi y là số lượng ô tô tiêu thụ trong tháng x (x ∈ {1; 2; 3; 4; 5}) thì y có phải là một hàm số của x không? Tính giá trị của y khi x = 5.
| Đây là một ví dụ về hàm số cho bằng biểu đồ: Số lượng ô tô tiêu thụ là hàm số của tháng.
|
(Trang 42)
2 MẶT PHẲNG TOẠ ĐỘ
Ở lớp 7 các em đã biết mỗi điểm trên trục số biểu diễn một số thực nào đó và ngược lại, mỗi số thực sẽ được biểu diễn bởi một điểm trên trục số. Liệu chúng ta có thể xác định được vị trí của một điểm bất kì trên mặt phẳng bằng cách tương tự không nhỉ?
Nhận biết toạ độ của một điểm trong mặt phẳng toạ độ
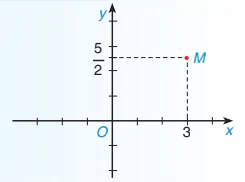
| Trên mặt phẳng, ta vẽ hai trục số Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục số như Hình 7.2. Các trục Ox và Oy gọi là các trục toạ độ, Ox thường vẽ nằm ngang và gọi là trục hoành, Oy thường vẽ thẳng đứng và gọi là trục tung, giao điểm O gọi là gốc toạ độ. Mặt phẳng có hệ trục toạ độ Oxy gọi là mặt phẳng toạ độ. Lấy một điểm M bất kì trong mặt phẳng toạ độ Oxy. Từ M kẻ các đường thẳng vuông góc với các trục toạ độ. Giả sử các đường vuông góc này cắt trục hoành tại điểm 3 và cắt trục tung tại điểm 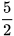 gọi là tung độ của điểm M. gọi là tung độ của điểm M. |
Hình 7.2
|
Trong mặt phẳng toạ độ, mỗi điểm M xác định duy nhất một cặp số (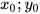 ) và mỗi cặp số (
) và mỗi cặp số (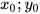
Cặp số (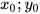 ) gọi là toạ độ của điểm M và kí hiệu là M(
) gọi là toạ độ của điểm M và kí hiệu là M(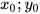 ), trong đó
), trong đó 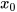 là hoành độ và
là hoành độ và 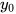 là tung độ của điểm M.
là tung độ của điểm M.
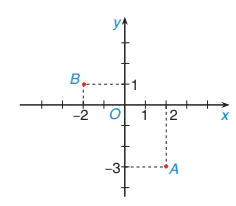
| Hãy cho biết toạ độ của gốc toạ độ O. Ví dụ 3 a) Viết toạ độ của các điểm A, B trong Hình 7.3. b) Xác định các điểm C(0; -2) và D(-1; 0) trong Hình 7.3. Giải a) Ta có toạ độ của hai điểm A, B là: A(2; –3), B(-2; 1). |
Hình 7.3 |
(Trang 43)
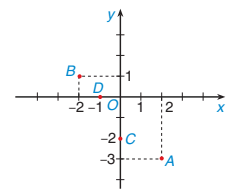
| b) Các điểm C(0; -2), D(-1; 0) được xác định như Hình 7.4.
Hình 7.4 |
|
Luyện tập 2
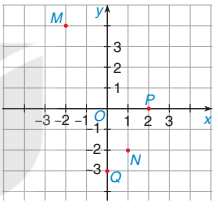
| a) Xác định toạ độ của các điểm M, N, P, Q trong Hình 7.5. b) Xác định các điểm R(2; -2) và S(-1; 2) trong Hình 7.5. Chú ý. Hệ trục toạ độ Oxy chia mặt phẳng toạ độ thành 4 góc phần tư (góc phần tư thứ I, II, III, IV) như Hình 7.6. |
Hình 7.5 |
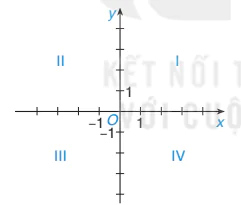
Hình 7.6
Tranh luận
| Những điểm có cả hoành độ và tung độ đều âm nằm ở góc phần tư thứ mấy?
| Em nghĩ là nằm ở góc phần tư thứ II.
| Không đúng, em nghĩ là nằm ở góc phần tư thứ III.
|
Ý kiến của em như thế nào?
(Trang 44)
3 ĐỒ THỊ CỦA HÀM SỐ
Nhận biết khái niệm đồ thị của hàm số
HĐ3 Hàm số y = f(x) được cho bởi bảng sau:
| x | -2 | -1 | 0 | 1 | 2 |
| y = f(x) | -1 | 0 | 1 | 2 | 3 |
a) Viết tập hợp {(x; y)} các cặp giá trị tương ứng của x và y.
b) Vẽ hệ trục toạ độ Oxy và biểu diễn các điểm có toạ độ là các cặp số trên. Tập hợp các điểm này gọi là đồ thị của hàm số y = f(x) đã cho.
| Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; y) trên mặt phẳng toạ độ. |
Ví dụ 4 Vẽ đồ thị của hàm số y = f(x) cho bởi bảng sau:
Giải Đồ thị của hàm số y = f(x) gồm bốn điểm như Hình 7.7. |
Hình 7.7 |
Luyện tập 3
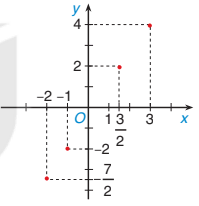
Vẽ đồ thị của hàm số y = f(x) cho bởi bảng sau:
| x | -3 | -1 | 1 | 2,5 |
| y | 4 | 3,5 | 1 | 0 |
BÀI TẬP
7.18. Các giá trị tương ứng của hai đại lượng x và y cho bởi các bảng sau. Đại lượng y có phải là một hàm số của x không?
a)
| x | -3 | -1 | 0 | 2 | 4 |
| y | 1 | 1 | 1 | 1 | 1 |
b)
| x | -2 | 1 | 0 | 1 | 2 |
| y | -2 | 1 | 0 | 2 | 2 |
(Trang 45)
7.19. Cho hàm số 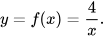
a) Tính f(–4); f(8).
b) Hoàn thành bảng sau vào vở:
| x | -2 | ? | 2 | 3 | ? |
| y=f(x) | ? | -4 | ? | ? | 8 |
7.20. a) Xác định toạ độ của các điểm A; B; C; D trong Hình 7.8.
b) Xác định các điểm E(0; -2) và F(2; −1) trong Hình 7.8.
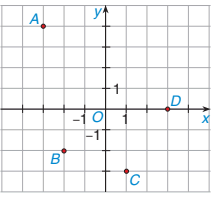
Hình 7.8
7.21. Hàm số y = f(x) được cho bởi bảng sau:
| x | -2 | -1 | 0 | 1 | 2 |
| y=f(x) | -5 | -2,5 | 0 | 2,5 | 5 |
Vẽ đồ thị của hàm số y=f(x).
7.22. Cân nặng và tuổi của bốn bạn An, Bình, Hưng, Việt được biểu diễn trên mặt phẳng toạ độ như Hình 7.9.
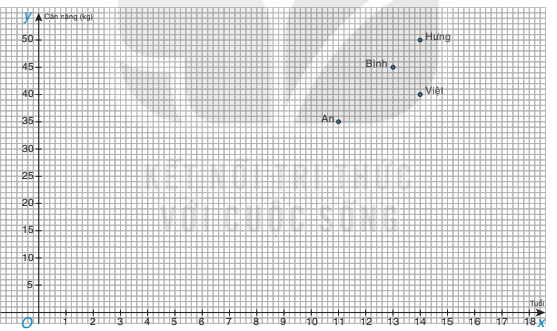
Hình 7.9
(Do số liệu về tuổi và cân nặng rất chênh lệch nên trong Hình 7.9, ta đã lấy một đơn vị dài trên trục tung bằng 5 lần đơn vị dài trên trục hoành).
Hãy cho biết:
a) Ai là người nặng nhất và nặng bao nhiêu?
b) Ai là người ít tuổi nhất và bao nhiêu tuổi?
c) Bình và Việt ai nặng hơn và ai nhiều tuổi hơn?
d) Thay dấu “?” bằng số thích hợp để hoàn thành bảng sau vào vở:
(Trang 46)
| Tên | An | Bình | Hưng | Việt |
| Tuổi | ? | ? | ? | ? |
| Cân nặng (kg) | ? | ? | ? | ? |
Theo bảng đã hoàn thành, cân nặng có phải là hàm số của tuổi không? Vì sao?
7.23. Hình 7.10 là đồ thị của hàm số mô tả nhiệt độ T (°C) tại các thời điểm t (giờ) của một thành phố ở châu Âu từ giữa trưa đến 6 giờ tối.
a) Tìm T(1), T(2), T(5) và giải thích ý nghĩa của các số này.
b) Trong hai giá trị T(1) và T(4), giá trị nào lớn hơn?
c) Tìm t sao cho T(t) = 5.
d) Trong khoảng thời gian nào thì nhiệt độ cao hơn 5 °C?
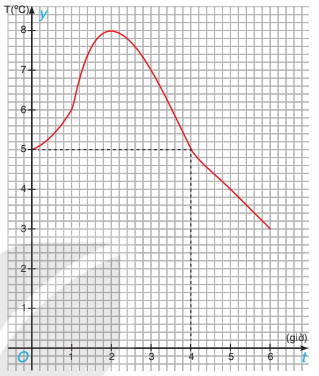
Hình 7.10
EM CÓ BIẾT ?
Nhà toán học René Descartes (1596 - 1650)
René Descartes là nhà triết học, nhà khoa học, nhà toán học người Pháp. Ông sinh ngày 31 tháng 3 năm 1596 ở La Haye en Touraine, ngày nay là vùng Descartes. Ông mất ngày 11 tháng 2 năm 1650 tại Stockholm, Thuỵ Điển.

René Descartes (1596-1650)
Đóng góp lớn nhất trong toán học của Descartes là đã giới thiệu khái niệm hệ toạ độ, ngày nay thường gọi là hệ toạ độ Descartes, cung cấp công cụ để có thể dùng đại số trong việc nghiên cứu hình học, giúp thống nhất đại số và hình học Euclid. Đóng góp này của ông có ảnh hưởng lớn đến sự phát triển của các lĩnh vực như hình học giải tích, phép tính vi tích phân và khoa học bản đồ.
Descartes cũng có những đóng góp về lí thuyết các đẳng thức. Ông là người đầu tiên đề xuất việc sử dụng những chữ cái cuối cùng của bảng chữ cái Latinh để chỉ các ẩn số và dùng những chữ cái đầu tiên của bảng chữ cái để chỉ các giá trị đã biết. Ông cũng đã sáng tạo ra hệ thống kí hiệu để mô tả luỹ thừa của các số (chẳng hạn trong biểu thức x^). Mặt khác, chính ông đã thiết lập ra phương pháp, gọi là phương pháp dấu hiệu Descartes, để tìm số nghiệm âm và số nghiệm dương của một đa thức bất kì.











































Bình Luận
Để Lại Bình Luận Của Bạn