Luyện tập chung bài 37 | Toán 8 - Tập 2 | Chương IX: Tam giác đồng dạng - Lớp 8 - Kết Nối Tri Thức Với Cuộc Sống

(Trang 108)

Ví dụ 1

Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 5 cm, AH = 4 cm.

a) Chứng minh △AHB ᔕ △CHA.

b) Tính độ dài các đoạn thẳng BH, CH, AC.

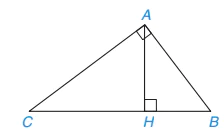
Hình 9.73

Giải. (H.9.73)

a) Xét tam giác AHB vuông tại H và tam giác CHA vuông tại H, ta có:

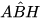= 90° - = - =

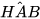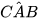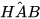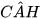
Vậy △AHB ᔕ △CHA (cặp góc nhọn bằng nhau).

b) Áp dụng định lí Pythagore cho tam giác vuông AHB, ta có:

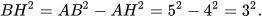
Suy ra BH = 3 cm.

Mặt khác, vì △AHB ᔕ △CHA nên 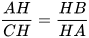. Suy ra 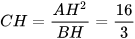(cm).

Đồng thời, 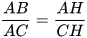. Do đó,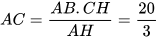

Ví dụ 2

Cho tam giác ABC có AB = 4 cm, AC = 3 cm, BC = 5 cm. Cho AH là đường cao của tam giác ABC. Chứng minh rằng:

a);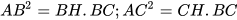

b) 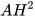= BH. CH;

c) Gọi M, N lần lượt là trung điểm của AH, BH. Chứng minh rằng △ANB ᔕ △CMA.

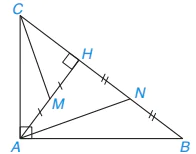
Hình 9.74

Giải. (H.9.74)

Từ giả thiết, ta thấy .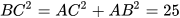

Theo định lí Pythagore đảo thì ABC là tam giác vuông tại A.

a) Tam giác AHB vuông tại H và tam giác CAB vuông tại A có: góc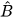

(Trang 109)

Do đó 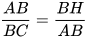, hay 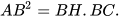Tương tự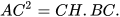

b) Tam giác AHB vuông tại H và tam giác CHA vuông tại H có: 

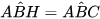= 90° -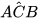

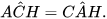
Vậy △AHB ᔕ △CHA (một góc nhọn bằng nhau). Do đó 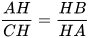, hay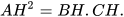

c) Vì △AHB ᔕ △CHA nên 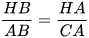và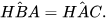

HaI tam giác ANB và CMA có:

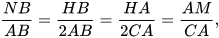
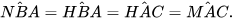
Vậy △ANB ᔕ △CMA (c.g.c)

Nhận xét. Cho △ABC vuông tại A có đường cao AH với BC = a, AC = b, AB = c, BH = b', CH = c', AH = h. Theo chứng minh câu a và câu b của Ví dụ 2 ta suy ra 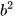= ab'; 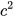= ac';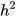

BÀI TẬP

9.32. Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH = 16 cm, CH = 9 cm.

a) Tính độ dài đoạn thẳng AH.

b) Tính độ dài các đoạn thẳng AB và AC.

9.33. Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Cho điểm M nằm trên cạnh BC sao cho BM = 4 cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB tại P.

a) Chứng minh rằng △BMP ᔕ △MCN.

b) Tính độ dài đoạn thẳng AM.

9.34. Trong Hình 9.75, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC.

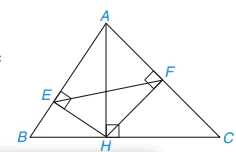
Hình 9.75

Chứng minh rằng:

a) △AEH ᔕ △AHB;                    b) △AFH ᔕ △AHC;

c) △AFE ᔕ △ABC.

9.35. Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt là trung điểm của AB và AC. Chứng minh △HBM ᔕ △HAN.

9.36. Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3 m.

a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét?

b) Vào buổi chiều khi bóng bạn An dài 3 m, hỏi bóng cột cờ dài bao nhiêu mét?