Bài 5. Khảo sát sự biến thiên và vẽ đồ thị của hàm số | Bài giải GIẢI TÍCH 12 | CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ - Lớp 12 - Sách Bài Giải

Câu hỏi 1 trang 32 SGK

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số đã học

y = ax + b              y = ax² + bx + c

theo sơ đồ trên.

Lời giải:

* Hàm số y = ax + b

Trường hợp a > 0

1. TXĐ: D = ℝ.

2. Sự biến thiên.

y’ = a > 0. Vậy hàm số đồng biến trên toàn bộ ℝ.

Ta có:  

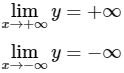
Bảng biến thiên:

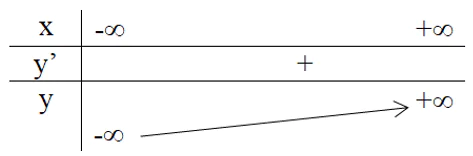
3. Vẽ đồ thị

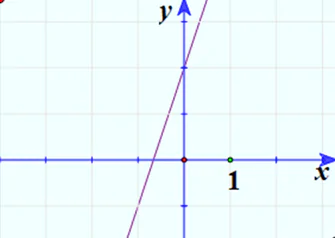
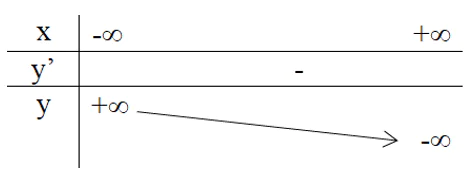
Trường hợp a < 0

1. TXĐ: D = ℝ.

2. Sự biến thiên.

y’ = a < 0. Vậy hàm số đồng biến trên toàn bộ ℝ.

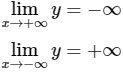
Bảng biến thiên:

3. Vẽ đồ thị

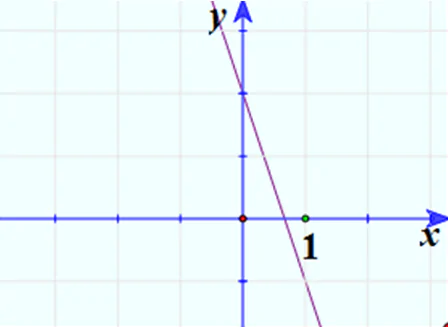
* Hàm số y = ax2 + bx + c

Trường hợp a > 0

1. TXĐ: D = ℝ.

2. Sự biến thiên.

y’ = 2ax + b. Cho y’ = 0 thì x = −b/2a

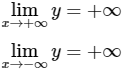
Bảng biến thiên:

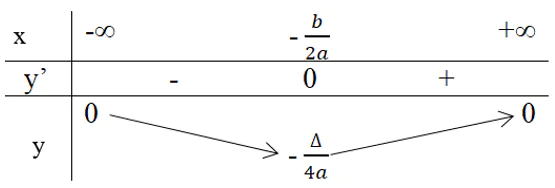
Hàm số nghịch biến trên khoảng (-∞, −b/2a).

Hàm số đồng biến trên khoảng [−b/2a, +∞].

Hàm số đạt cực tiểu bằng −Δ/4a tại x = −b/2a.

3. Vẽ đồ thị:

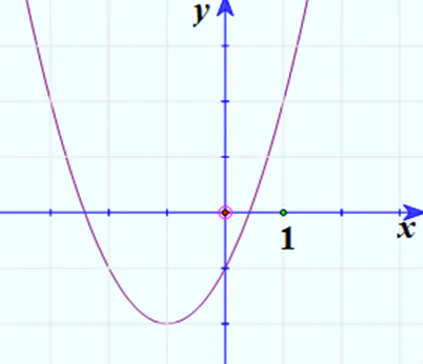
Trường hợp a < 0

1. TXĐ: D = ℝ.

2. Sự biến thiên.

y’ = 2ax + b. Cho y’ = 0 thì x = −b/2a.

Bảng biến thiên:

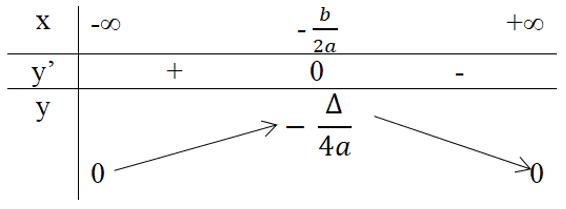
Hàm số đồng biến trên khoảng (-∞, −b/2a).

Hàm số nghịch biến trên khoảng [−b/2a, +∞].

Hàm số đạt cực đại bằng −Δ/4a tại x = −b/2a.

3. Vẽ đồ thị:

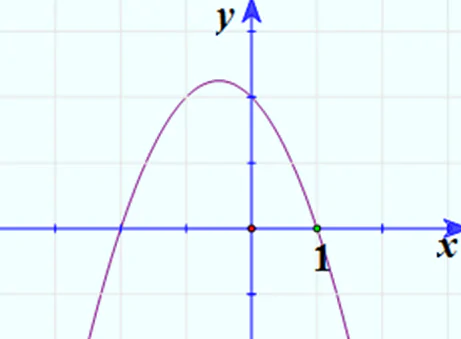
Câu hỏi 2 trang 33 SGK

Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = -x³ + 3x² – 4. Nêu nhận xét về đồ thị của hàm số này với đồ thị của hàm số khảo sát trong Ví dụ 1.

Lời giải:

1.TXĐ: D = R.

2. Sự biến thiên:

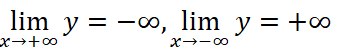
y’ = -3x² + 6x. Cho y’ = 0 ⇒ x = 0 hoặc x = 2.

Bảng biến thiên:

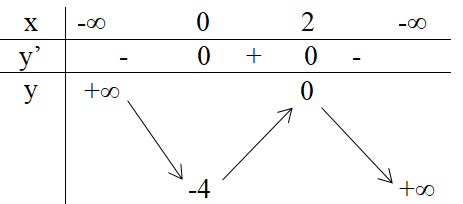
Hàm số đồng biến trên khoảng (0 , 2)

Hàm số nghịch biến trên các khoảng (-∞ , 0), (2 ,+ ∞).

Hàm số đạt cực đại bằng 0 tại x = 2.

Hàm số đạt cực tiểu bằng -4 tại x = 0.

3. Đồ thị

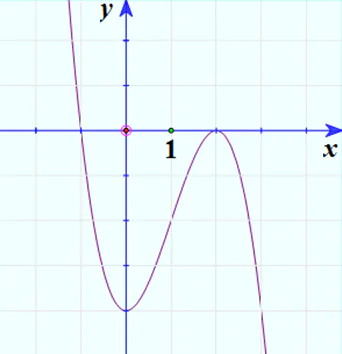
Nhận xét: hai đồ thị đối xứng nhau qua Oy.

Câu hỏi 3 trang 35 SGK

Khảo sát sự biến thiên và vẽ đồ thị hàm số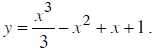

Lời giải:

1.TXĐ: D = ℝ.

2. Sự biến thiên:

Ta có: y’ = x² – 2x + 1 = (x - 1)² ≥ 0 với mọi x.

Vậy hàm số đồng biến trên toàn bộ ℝ.

Cho y’ = 0 ⇒ x = 1.

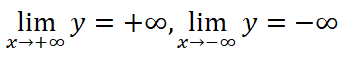
Bảng biến thiên

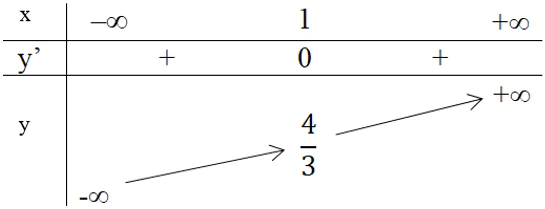
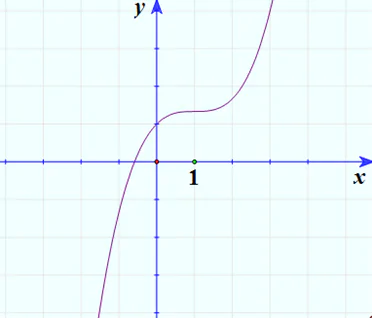
3. Đồ thị

 

Câu hỏi 4 trang 36 SGK

Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = -x⁴ + 2x² + 3.

Bằng đồ thị, biện luận theo m số nghiệm của phương trình -x⁴ + 2x² + 3 = m.

Lời giải:

1.TXĐ: D = R.

2. Sự biến thiên:

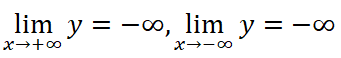
y’ = -4x³ + 4x. Cho y’ = 0 ⇒ x = 0 hoặc x = ±1.

Bảng biến thiên:

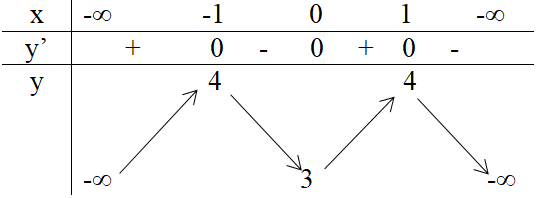
Hàm số đồng biến trên: (-∞ ,-1), (0 , 1).

Hàm số nghịch biến trên: (-1 , 0), (1 , +∞).

Hàm số đạt cực đại bằng 4 tại x = -1 và x = 1.

Hàm số đạt cực tiểu bằng 3 tại x = 0.

3. Đồ thị

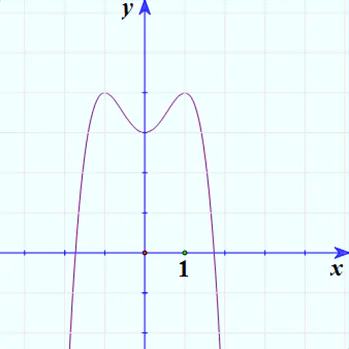
Giải biện luận phương trình -x⁴ + 2x² + 3 = m.

Số giao điểm của hai đồ thị y = -x⁴ + 2x² + 3 và y = m là số nghiệm của phương trình trên.

Với m > 4. Hai đồ thị không giao nhau nên phương trình vô nghiệm.

Với m = 4 và m < 3. Hai đồ thị giao nhau tại 2 điểm phân biệt nên phương trình có hai nghiệm phân biệt.

Với m = 3. Hai đồ thị giao nhau tại 3 điểm phân biệt nên phương trình có ba nghiệm phân biệt.

Với 3 < m < 4. Hai đồ thị giao nhau tại 4 điểm phân biệt nên phương trình có bốn nghiệm phân biệt.

Câu hỏi 5 trang 38 SGK

Lấy một ví dụ về hàm số có dạng y = ax⁴ + bx² + c sao cho phương trình y’ = 0 chỉ có một nghiệm.

Lời giải:

Ví dụ hàm số y = x⁴. Có đạo hàm y’ = 4x³. Cho y’ = 0 thì x = 0.

Câu hỏi 6 trang 42 SGK

Tìm tọa độ giao điểm của đồ thị hai hàm số

y = x² + 2x – 3

y = -x² – x + 2.

Lời giải:

Xét phương trình tương giao:

-x² – x + 2 = x² + 2x – 3

⇔ 2x² + 3x – 5 = 0

⇔ x = 1 hoặc x =−5/2

Với x = 1 thì y = 1² + 2.1 – 3 = 1 + 2 – 3 = 0

Với x = −5/2 thì y = (−5/2)² + 2.(−5/2) − 3 = −7/4

Vậy tọa độ giao điểm là (1 , 0) và (−5/2 , −7/4)

Bài 1 trang 43 SGK

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc ba sau:

a) y = 2 + 3x - x³;

b) y = x³ + 4x² + 4x;

c) y = x³ + x² + 9x;

d) y = -2x³ + 5.

Lời giải:

a) Hàm số y = -x³ + 3x + 2.

1) Tập xác định: D = R

2) Sự biến thiên:

+ Chiều biến thiên:

y' = -3x² + 3.

y' = 0 ⇔ x = ±1.

Trên các khoảng (-∞ ; -1) và (1 ; +∞), y’ < 0 nên hàm số nghịch biến.

Trên (-1 ; 1), y’ > 0 nên hàm số đồng biến.

+ Cực trị :

Hàm số đạt cực đại tại x = 1, y_CĐ = 4 ;

Hàm số đạt cực tiểu tại x = -1 ; y_CT = 0.

+ Giới hạn:

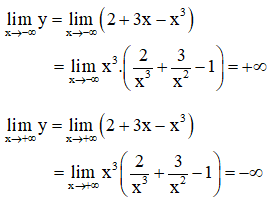
+ Bảng biến thiên:

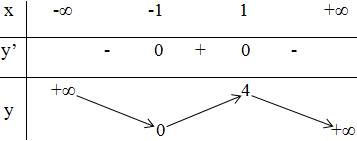
3) Đồ thị:

Ta có : 2 + 3x – x3 = 0 ⇔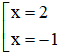

Vậy giao điểm của đồ thị với trục Ox là (2 ; 0) và (-1 ; 0).

y(0) = 2 ⇒ giao điểm của đồ thị với trục Oy là (0 ; 2).

Đồ thị hàm số :

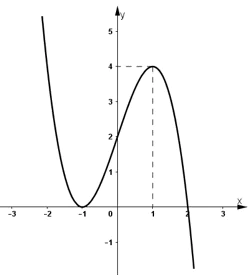
b) Hàm số y = x³ + 4x² + 4x.

1) Tập xác định: D = ℝ

2) Sự biến thiên:

y' = 3x2 + 8x + 4;

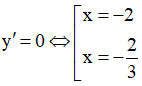
Trên các khoảng (-∞ ; -2) và (−2/3 ; +∞) thì y’ > 0 nên hàm số đồng biến.

Trên (-2 ; −2/3) thì y’ < 0 nên hàm số nghịch biến.

+ Cực trị:

Hàm số đạt cực đại tại x = -2, y_CD = 0;

Hàm số đạt cực tiểu tại x = −2/3; y_CT = −32/27.

+ Giới hạn:

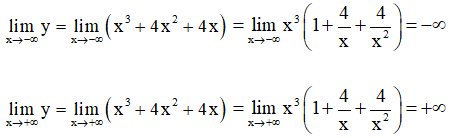
+ Bảng biến thiên:

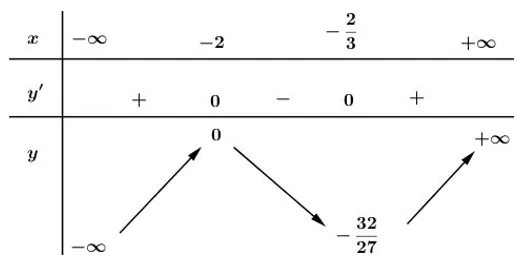
3) Đồ thị:

Ta có : x³ + 4x² + 4x = 0 ⇔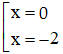

Vậy giao điểm của đồ thị với Ox là (0 ; 0) và (-2 ; 0).

Đồ thị hàm số :

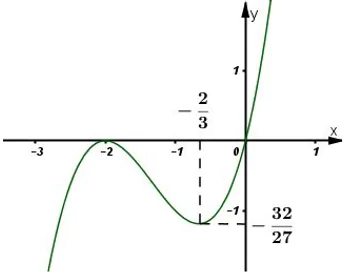
c) Hàm số y = x³ + x² + 9x.

1) Tập xác định: D = R

2) Sự biến thiên:

+ Chiều biến thiên:

y' = 3x² + 2x + 9 > 0

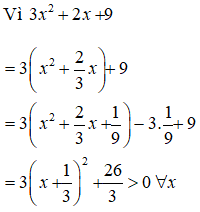
⇒ Hàm số luôn đồng biến trên R.

+ Hàm số không có cực trị.

+ Giới hạn:

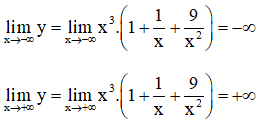
+ Bảng biến thiên:

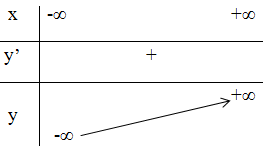
3) Đồ thị hàm số.

+ Đồ thị hàm số cắt trục Ox tại (0 ; 0).

+ Đồ thị hàm số đi qua (1 ; 11) ; (-1 ; -9)

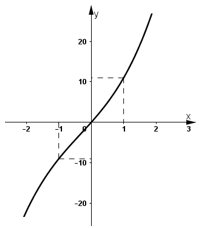
d) Hàm số y = 2x³ + 5.

1) Tập xác định: D = R

2) Sự biến thiên:

+ Chiều biến thiên:

y' = 6x² ≥ 0 ∀ x ∈ R

Hàm số đồng biến trên R

Hàm số không có cực trị.

+ Giới hạn:

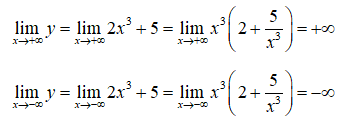
+ Bảng biến thiên:

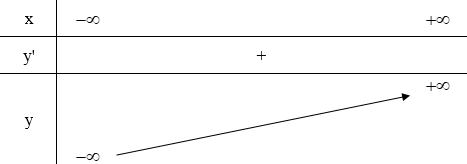
3) Đồ thị:

Đồ thị hàm số cắt trục tung tại (0 ; 5)

Đồ thị hàm số đi qua điểm (1 ; 7) và (-1 ; 3)

Kiến thức áp dụng

Các bước khảo sát hàm số và vẽ đồ thị: 1. Tìm tập xác định. 2. Khảo sát sự biến thiên + Tính y’ ⇒ Chiều biến thiên của hàm số. + Tìm cực trị. + Tính các giới hạn Từ đó suy ra Bảng biến thiên. 3. Vẽ đồ thị hàm số.

Bài 2 trang 43 SGK

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:

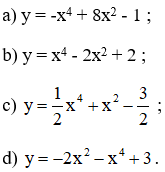
Lời giải:

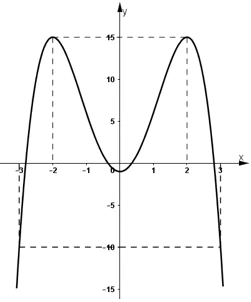
a) Hàm số y = -x⁴ + 8x² – 1.

1) Tập xác định: D = ℝ

2) Sự biến thiên:

+ Chiều biến thiên:

y' = -4x³ + 16x = -4x(x² - 4)

y' = 0 ⇔ -4x(x² - 4) = 0 ⇔ x = 0; x = ±2

Trên khoảng (-∞ ; -2) và (0 ; 2), y’ > 0 nên hàm số đồng biến.

Trên các khoảng (-2 ; 0) và (2 ; +∞), y’ < 0 nên hàm số nghịch biến.

+ Cực trị:

Hàm số đạt cực đại tại x = 2 và x = -2; y_CĐ = 15

Hàm số đạt cực tiểu tại x = 0; y_CT = -1.

+ Giới hạn:

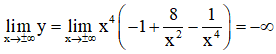
+ Bảng biến thiên:

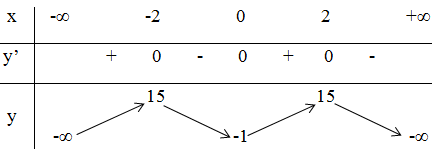
3) Đồ thị:

+ Hàm số đã cho là hàm số chẵn, vì:

y(-x) = -(-x)⁴ + 8(-x)² - 1 = -x⁴ + 8x² - 1 = y(x)

Suy ra đồ thị nhận Oy làm trục đối xứng.

+ Giao với Oy tại điểm (0 ; -1) (vì y(0) = -1).

+ Đồ thị hàm số đi qua (-3 ; -10) và (3 ; - 10).

b) Hàm số y = x⁴ – 2x² + 2.

1) Tập xác định: D = ℝ

2) Sự biến thiên:

+ Chiều biến thiên:

y' = 4x³ - 4x = 4x(x² - 1)

y' = 0 ⇔ 4x(x² - 1) = 0 ⇔ x = 0 ; x = ±1.

+ Giới hạn:

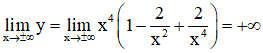
+ Bảng biến thiên:

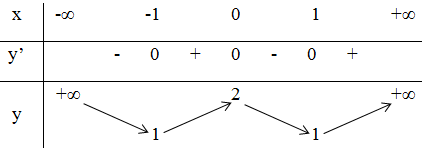
Kết luận:

Hàm số đồng biến trên khoảng (-1 ; 0) và (1 ; +∞).

Hàm số nghịch biến trên các khoảng (-∞ ; -1) và (0 ; 1).

Đồ thị hàm số có hai điểm cực tiểu là: (-1 ; 1) và (1 ; 1).

Đồ thị hàm số có điểm cực đại là: (0 ; 2)

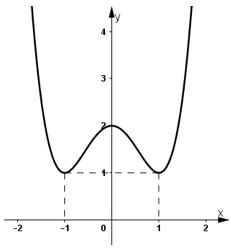
3) Đồ thị:

+ Hàm số chẵn nên đồ thị hàm số nhận trục Oy là trục đối xứng.

+ Đồ thị hàm số cắt trục tung tại (0 ; 2).

+ Đồ thị hàm số đi qua (-1 ; 1) và (1 ; 1).

+ Đồ thị hàm số:

c) Hàm số

1) Tập xác định: D = ℝ

2) Sự biến thiên:

+ y' = 2x³ + 2x = 2x(x² + 1)

   y' = 0 ⇔ 2x(x² + 1) = 0 ⇔ x = 0

+ Giới hạn:

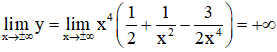
+ Bảng biến thiên:

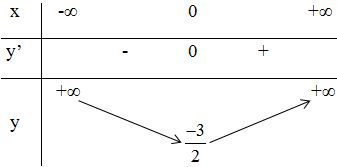
Kết luận:

Hàm số đồng biến trên khoảng (0 ; +∞).

Hàm số nghịch biến trên các khoảng (-∞ ; 0).

Đồ thị hàm số có điểm cực đại là:.

3) Đồ thị:

+ Hàm số chẵn nên nhận trục Oy là trục đối xứng.

+ Hàm số cắt trục hoành tại điểm (-1 ; 0) và (1 ; 0).

+ Hàm số cắt trục tung tại điểm

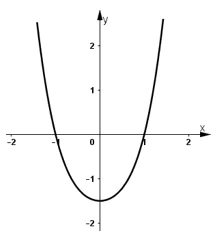
d) Hàm số y = -2x² – x⁴ + 3.

1) Tập xác định: D = ℝ

2) Sự biến thiên:

+ Chiều biến thiên:

y' = -4x - 4x³ = -4x(1 + x²)

y' = 0 ⇔ -4x(1 + x²) = 0 ⇔ x = 0

+ Giới hạn:

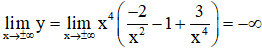
+ Bảng biến thiên:

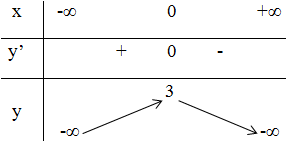
Kết luận:

Hàm số đồng biến trên khoảng (-∞ ; 0).

Hàm số nghịch biến trên các khoảng (0 ; +∞).

Đồ thị hàm số có điểm cực đại là: (0 ; 3).

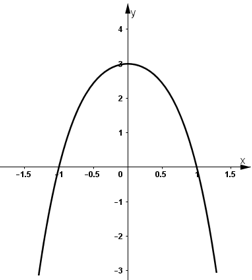
3) Đồ thị:

+ Hàm số là hàm số chẵn nên nhận trục Oy là trục đối xứng.

+ Hàm số cắt trục Ox tại (-1 ; 0) và (1 ; 0).

+ Hàm số cắt trục Oy tại (0 ; 3).

Bài 3 trang 43 SGK

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số phân thức:

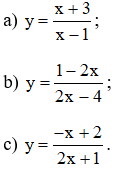
Lời giải:

a) Hàm số

1) Tập xác định: D = ℝ \ {1}

2) Sự biến thiên:

+ Chiều biến thiên:

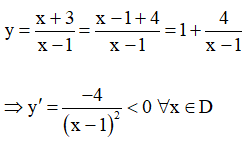
Suy ra hàm số nghịch biến trên (-∞ ; 1) và (1 ; +∞).

+ Cực trị: Hàm số không có cực trị.

+ Tiệm cận:

Suy ra x = 1 là tiệm cận đứng.

Lại có:

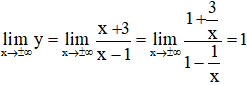
Suy ra y = 1 là tiệm cận ngang.

+ Bảng biến thiên:

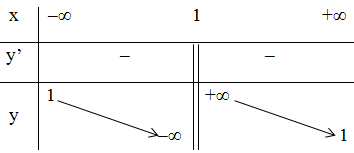
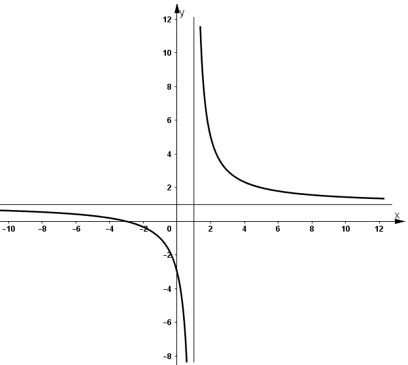
3) Đồ thị:

+ Giao với Oy: (0 ; -3)

+ Giao với Ox: (-3 ; 0)

+ Đồ thị nhận (1 ; 1) là tâm đối xứng.

b) Hàm số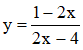

1) Tập xác định: D = ℝ \ {2}

2) Sự biến thiên:

+ Chiều biến thiên:

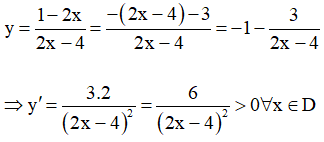
Suy ra hàm số đồng biến trên (-∞ ; 2) và (2 ; +∞).

+ Cực trị: Hàm số không có cực trị.

+ Tiệm cận:

Suy ra x = 2 là tiệm cận đứng của đồ thị hàm số.

Lại có:

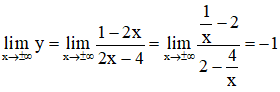
Suy ra y = -1 là tiệm cận ngang.

+ Bảng biến thiên:

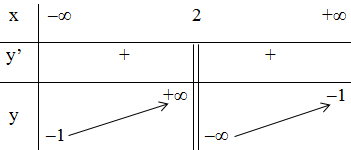
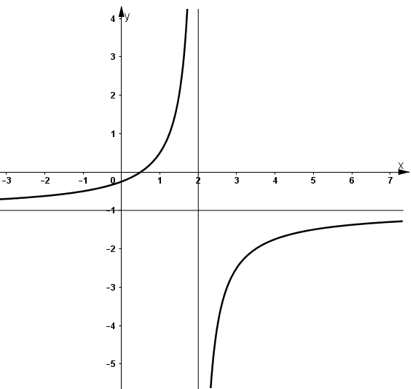
3) Đồ thị:

+ Giao với Oy: (0 ; −1/4)

+ Giao với Ox: (1/2 ; 0)

+ Đồ thị hàm số nhận (2; -1) là tâm đối xứng.

c) Hàm số

1) Tập xác định: D = ℝ \ {-1/2}

2) Sự biến thiên:

+ Chiều biến thiên:

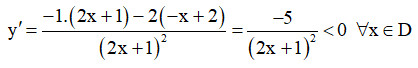
Suy ra hàm số nghịch biến trên (-∞; −1/2) và (−1/2 ; +∞).

+ Cực trị: Hàm số không có cực trị.

+ Tiệm cận:

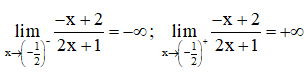
Suy ra  là tiệm cận đứng của đồ thị hàm số.

Lại có:

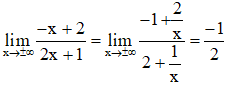
Suy ra là tiệm cận ngang của đồ thị hàm số.

+ Bảng biến thiên:

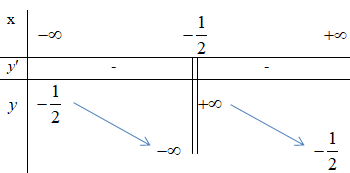
3) Đồ thị:

+ Giao với Oy: (0 ; 2)

+ Giao với Ox: (2 ; 0)

+ Đồ thị hàm số nhận (−1/2 ; −1/2) là tâm đối xứng.

Bài 4 trang 44 SGK

Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau:

a) x³ - 3x² + 5 = 0;

b) -2x³ + 3x² - 2 = 0;

c) 2x² - x⁴ = -1.

Lời giải:

a) Xét y = f(x) = x³ - 3x² + 5 (1)

- TXĐ: D = R

- Sự biến thiên:

+ Chiều biến thiên:

f'(x) = 3x² - 6x = 3x(x - 2)

f'(x) = 0 ⇔ x = 0 ; x = 2

+ Giới hạn:

+ Bảng biến thiên:

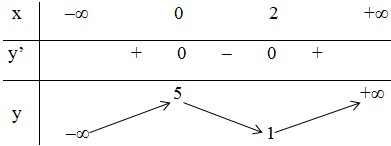
- Đồ thị:

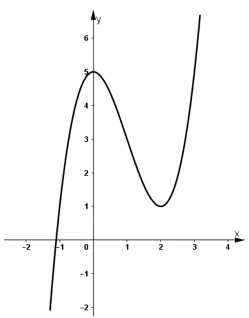
Đồ thị hàm số y = f(x) cắt trục hoành tại 1 điểm duy nhất.

⇒ phương trình x³ - 3x² + 5 = 0 chỉ có 1 nghiệm duy nhất.

b) Xét hàm số y = f(x) = -2x³ + 3x² – 2.

- TXĐ: D = R

- Sự biến thiên:

+ Chiều biến thiên:

y' = -6x² + 6x = -6x(x - 1)

y' = 0 ⇔ x = 0 ; x = 1

+ Giới hạn:

+ Bảng biến thiên:

 

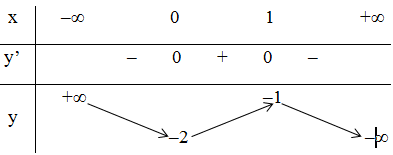
- Đồ thị:

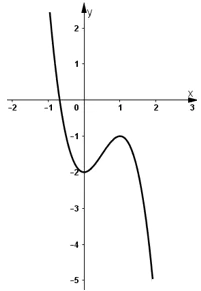
Đồ thị hàm số y = f(x) cắt trục hoành tại 1 điểm duy nhất

⇒ phương trình f(x) = 0 có nghiệm duy nhất.

Vậy phương trình -2x³ + 3x² - 2 = 0 chỉ có một nghiệm.

c) Xét hàm số y = f(x) = 2x² - x4

- TXĐ: D = ℝ

- Sự biến thiên:

+ Chiều biến thiên:

y' = 4x - 4x³ = 4x(1 - x²)

y' = 0 ⇔ x = 0 ; x = ±1

+ Giới hạn:

+ Bảng biến thiên:

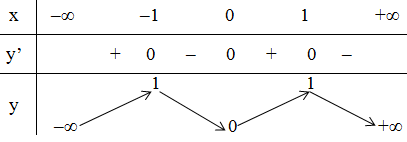
- Đồ thị:

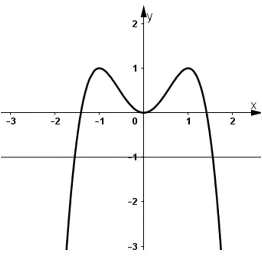
Đồ thị hàm số y = f(x) cắt đường thẳng y = -1 tại hai điểm.

Suy ra phương trình f(x) = -1 có hai nghiệm phân biệt.

Vậy phương trình đã cho có 2 nghiệm phân biệt.

Kiến thức áp dụng

Số nghiệm của phương trình f(x) = m phụ thuộc vào số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m.

Bài 5 trang 44 SGK

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số

y = -x³ + 3x + 1

b) Dựa vào đồ thị (C), biện luận về số nghiệm của phương trình sau theo tham số m:

x³ - 3x + m = 0

Lời giải:

a) Khảo sát hàm số y = -x³ + 3x + 1

- Tập xác định: D = R

- Sự biến thiên:

+ Chiều biến thiên:

y' = -3x² + 3 = -3(x² - 1)

y' = 0 ⇔ -3(x² - 1) = 0 ⇔ x = ±1.

+ Giới hạn:

+ Bảng biến thiên:

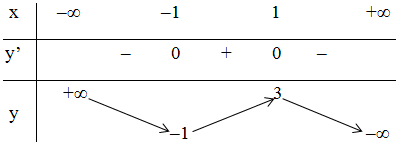
Kết luận:

Hàm số đồng biến trên khoảng (-1 ; 1).

Hàm số nghịch biến trên các khoảng (-∞ ; -1) và (1 ; +∞).

Hàm số đạt cực tiểu tại x = -1 ; y_CT = -1.

Hàm số đạt cực đại tại x = 1 ; y_CĐ = 3.

- Đồ thị:

+ Giao với Oy: (0 ; 1).

+ Đồ thị (C) đi qua điểm (-2 ; 3), (2 ;-1).

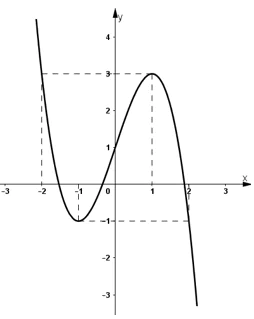
b) Ta có: x³ - 3x + m = 0 (*)

⇔ -x³ + 3x + 1 = m + 1

Số nghiệm của phương trình (*) phụ thuộc số giao điểm của đồ thị hàm số y = -x³ + 3x + 1 và đường thẳng y = m + 1.

Kết hợp với quan sát đồ thị hàm số ta có:

+ Nếu m + 1 < –1 ⇔ m < –2

⇒ (C ) cắt (d) tại 1 điểm.

⇒ phương trình (*) có 1 nghiệm.

+ Nếu m + 1 = –1 ⇔ m = –2

⇒ (C ) cắt (d) tại 2 điểm

⇒ phương trình (*) có 2 nghiệm.

+ Nếu –1 < m + 1 < 3 ⇔ –2 < m < 2

⇒ (C ) cắt (d) tại 3 điểm.

⇒ phương trình (*) có 3 nghiệm.

+ Nếu m + 1 = 3 ⇔ m = 2

⇒ (C ) cắt (d) tại 2 điểm.

⇒ phương trình (*) có hai nghiệm.

+ Nếu m + 1 > 3 ⇔ m > 2

⇒ (C ) cắt (d) tại 1 điểm

⇒ phương trình (*) có một nghiệm.

Kết luận:

+ Với m < -2 hoặc m > 2 thì phương trình có 1 nghiệm.

+ Với m = -2 hoặc m = 2 thì phương trình có 2 nghiệm.

+ Với -2 < m < 2 thì phương trình có 3 nghiệm.

Kiến thức áp dụng

- Các bước khảo sát hàm số và vẽ đồ thị: 1. Tìm tập xác định. 2. Khảo sát sự biến thiên + Tính y’ ⇒ Chiều biến thiên của hàm số. + Tìm cực trị. + Tính các giới hạn Từ đó suy ra Bảng biến thiên. 3. Vẽ đồ thị hàm số. - Số nghiệm của phương trình f(x) = m phụ thuộc vào số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m.

Bài 6 trang 44 SGK

Cho hàm số

a) Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn đồng biến trên mỗi khoảng xác định của nó.

b) Xác định m để tiệm cận đứng của đồ thị đi qua A(-1, √2).

c) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 2.

Lời giải:

TXĐ: D = ℝ \ {}

a) Với mọi tham số m ta có:

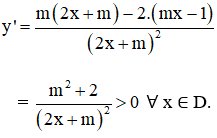
Vậy hàm số luôn đồng biến trên mỗi khoảng xác định của nó.

b) Ta có:

⇒

 là tiệm cận đứng của đồ thị hàm số.

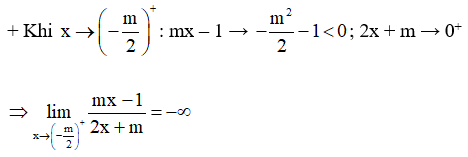
+ Tiệm cận đứng đi qua A(-1; √2)

⇔ ⇔ m = 2.

Vậy với m = 2 thì tiệm cận đứng của đồ thị đi qua A(-1; √2)

c) Với m = 2 ta được hàm số: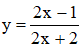

- TXĐ: D = ℝ \ {-1}

- Sự biến thiên:

+ Chiều biến thiên: Theo kết quả câu a)

Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞)

+ Cực trị: Hàm số không có cực trị.

+ Tiệm cận:

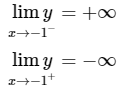
Suy ra đồ thị có tiệm cận đứng là x = -1.

Lại có

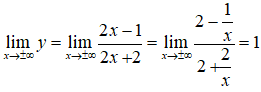
Suy ra đồ thị có tiệm cận ngang là y = 1.

+ Bảng biến thiên:

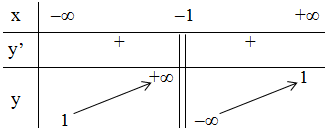
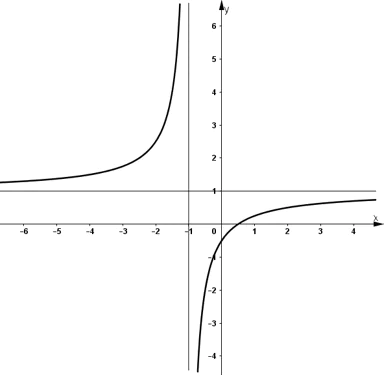
- Đồ thị:

+ Đồ thị cắt trục hoành tại (1/2 ; 0).

+ Đồ thị cắt trục tung tại (0 ; -1/2).

+ Đồ thị nhận I(-1 ; 1) là tâm đối xứng.

Kiến thức áp dụng

+ Hàm số y = f(x) có đạo hàm trên khoảng K xác định thì : f(x) đồng biến nếu f’(x) > 0 với ∀ x ∈ K. + Đường thẳng x = x0 là tiệm cận đứng của đồ thị hàm số y = f(x) nếu có   hoặc  .

Bài 7 trang 44 SGK

Cho hàm số _.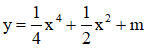

a) Với giá trị nào của tham số m, đồ thị của hàm đi qua điểm (-1 ; 1)?

b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1.

c) Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng 7/4.

Lời giải:

a) Đồ thị hàm số qua điểm (-1 ; 1)

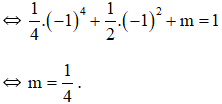
Vậy m = 1/4 thì đồ thị hàm số đi qua điểm (-1 ; 1).

b) Với m = 1, hàm số trở thành

- TXĐ: D = ℝ

- Sự biến thiên:

+ Chiều biến thiên:

y' = x³ + x = x(x² + 1)

y' = 0 ⇔ x(x² + 1) ⇔ x = 0

+ Giới hạn:

+ Bảng biến thiên:

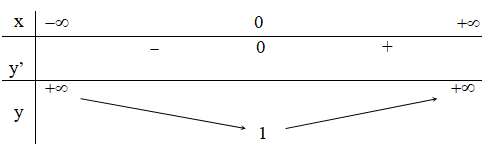
Kết luận:

Hàm số đồng biến trên (0 ; +∞)

Hàm số nghịch biến trên (-∞ ; 0)

Hàm số có điểm cực tiểu là (0 ; 1).

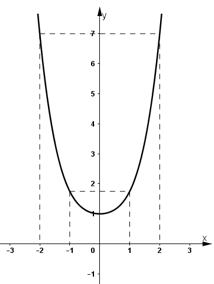
- Đồ thị:

+ Đồ thị nhận trục Oy là trục đối xứng.

+ Đồ thị cắt trục tung tại (0 ; 1).

+ Đồ thị hàm số đi qua (-1 ; 1,75); (1 ; 1,75); (-2 ; 7); (2 ; 7).

c) Điểm thuộc (C) có tung độ bằng 7/4 nên hoành độ của điểm đó là nghiệm của phương trình:

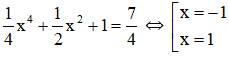
Có: y' = x³ + x

+ Phương trình tiếp tuyến của (C) tại :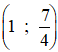

y’(1) = 2

⇒ Phương trình tiếp tuyến:  hay

+ Phương trình tiếp tuyến của (C) tại :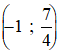

y’(-1) = -2.

⇒ Phương trình tiếp tuyến: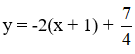

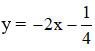
hay y =

Kiến thức áp dụng

- Các bước khảo sát hàm số và vẽ đồ thị: 1. Tìm tập xác định. 2. Khảo sát sự biến thiên + Tính y’ ⇒ Chiều biến thiên của hàm số. + Tìm cực trị. + Tính các giới hạn Từ đó suy ra Bảng biến thiên. 3. Vẽ đồ thị hàm số.   - Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại M(y0; f(y0)): y = f’(y0)(x – y0) + f(y0)

Bài 8 trang 44 SGK

Cho hàm số 

y = x³ + (m + 3)x² + 1 - m (m là tham số)

có đồ thị (C_m).

a) Xác định m để hàm số có điểm cực đại là x = -1.

b) Xác định m để đồ thị (C_m) cắt trục hoành tại x = -2.

Lời giải:

a) Xét hàm số y = x3 + (m + 3)x2 + 1 – m.

+ TXĐ : D = R.

+ y’ = 3x² + 2(m + 3).x

⇒ y’’ = 6x + 2(m + 3).

+ Hàm số có điểm cực đại là x = -1

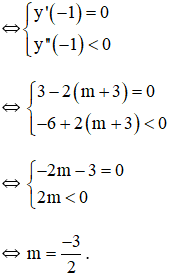
Vậy với thì hàm số có điểm cực đại là x = -1.

b) Đồ thị (C_m) cắt trục hoành tại x = -2

⇔ y(-2) = 0

⇔ (-2)³ + (m + 3)(-2)² + 1 - m = 0

⇔ -8 + 4(m + 3) + 1 - m = 0

⇔ 3m + 5 = 0

⇔

Vậy

 thì đồ thị (C_m) cắt trục hoành tại x = - 2.

Kiến thức áp dụng

Hàm số y = f(x) có đạo hàm cấp hai trong khoảng K, khi đó, với y0 ∈ K ta có: Nếu f’(y0) = 0 và f’’(y0) < 0 thì y0 là điểm cực đại.

Bài 9 trang 44 SGK

Cho hàm số 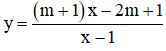(m là tham số)

có đồ thị (G).

a) Xác định m để đồ thị (G) đi qua điểm (0 ; -1).

b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m tìm được.

c) Viết phương trình tiếp tuyến của đồ thị trên tại giao điểm của nó với trục tung.

Lời giải:

a) Đồ thị (G) đi qua điểm (0 ; -1)

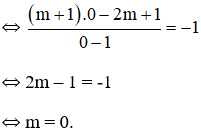
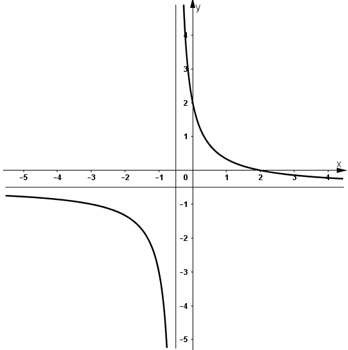
b) Với m = 0, hàm số trở thành: 

- TXĐ: D = R \ {1}

- Sự biến thiên:

+ Chiều biến thiên:

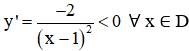
⇒ Hàm số nghịch biến trên (-∞; 1) và (1; +∞).

+ Cực trị: Hàm số không có cực trị.

+ Tiệm cận:

⇒ x = 1 là tiệm cận đứng của đồ thị hàm số.

⇒ y = 1 là tiệm cận ngang của đồ thị hàm số.

+ Bảng biến thiên:

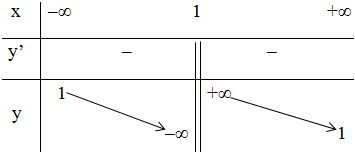
- Đồ thị:

+ Giao điểm với Ox: (-1 ; 0)

+ Giao điểm với Oy: (0 ; -1)

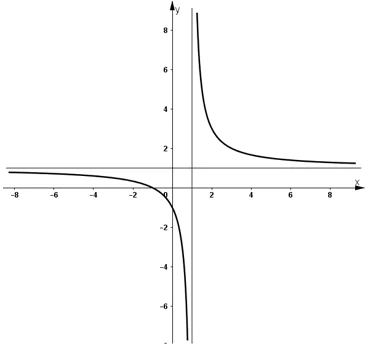
c) Đồ thị cắt trục tung tại điểm P(0 ; -1), khi đó phương trình tiếp tuyến tại điểm P(0 ; -1) là:

y = y'(0).(x – 0) – 1

hay y = -2x – 1

Vậy phương trình tiếp tuyến cần tìm là: y = -2x – 1.