Nội Dung Chính
Câu hỏi 1 trang 57 SGK
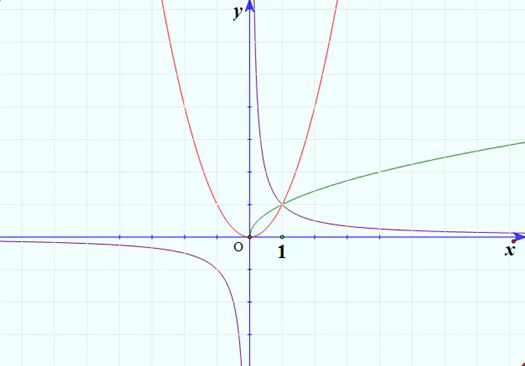
Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau và nêu nhận xét về tập xác định của chúng:
![]()
Lời giải:
Đồ thị của hàm số y = x2: đường màu đỏ.
Đồ thị của hàm số y = x1/2: đường màu xanh.
Đồ thị của hàm số y = x-1 đường màu tím.
 Ta có:
Ta có:
Tập xác định của hàm số y = x2 là D1 = ℝ.
Tập xác định của hàm số y = x1/2 là D2 = [0; +∞).
Tập xác định của hàm số y = x-1 là D3 = ℝ\{0}.
Câu hỏi 2 trang 57 SGK
Tính đạo hàm của các hàm số:
![]()
Lời giải:
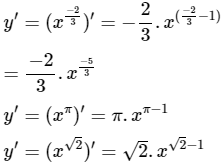
Câu hỏi 3 trang 58 SGK
Tính đạo hàm của hàm số ![]()
Lời giải:
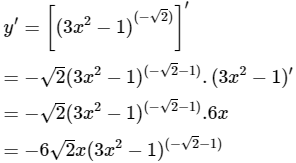
Bài 1 trang 60 SGK
Tìm tập xác định của các hàm số:

Lời giải:
a) Hàm số ![]() xác định
xác định
⇔ 1 – x > 0
⇔ x < 1.
Vậy tập xác định D = (-∞ ; 1).
b) Hàm số ![]() xác định
xác định
⇔ 2 – x2 > 0
⇔ x2 < 2
⇔ −√2< x <√2
Vậy tập xác định D = (−√2 ; √2).
c) Hàm số y = (x2 – 1)-2 xác định khi và chỉ khi:
x2 - 1 ≠ 0 ⇔ x2 ≠ 1 ⇔ x ≠ ±1
Vậy tập xác định của hàm số là D = R\ {-1; 1}.
d) Hàm số ![]() xác định
xác định
⇔ x2 – x – 2 > 0
⇔ (x + 1)(x – 2) > 0
⇔ x < -1 hoặc x > 2
Vậy tập xác định D = (-∞ ; -1) ∪ (2 ; +∞).
Kiến thức áp dụng
| 1. Khi xét lũy thừa với số mũ 0 hoặc số mũ nguyên âm thì cơ số phải khác 0. 2. Khi xét lũy thừa với số mũ không nguyên thì cơ số phải dương. |
Bài 2 trang 61 SGK
Tìm các đạo hàm của các hàm số:

Lời giải:
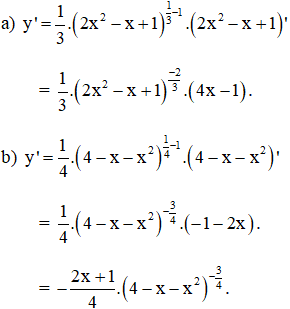
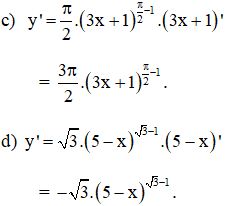
Kiến thức áp dụng
| Đạo hàm của hàm số y = uα là: y' = (uα)' = α.uα – 1.u' |
Bài 3 trang 61 SGK
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số:
![]()
Lời giải:
a) Xét hàm số ![]() ta có:
ta có:
- Tập khảo sát: (0 ; +∞).
- Sự biến thiên:
+ ![]()
Do đó, hàm số đã cho đồng biến trên tập xác định.
+ Giới hạn:
![]()
+ Tiệm cận: Đồ thị hàm số không có tiệm cận.
+ Bảng biến thiên:
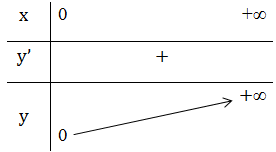
- Đồ thị hàm số:
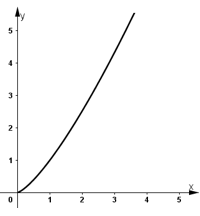
b) Xét hàm số y = x-3, ta có :
- Tập xác định: D = ℝ\{0}
- Sự biến thiên:
+ y' = -3.x-3 - 1 = -3.x-4 < 0 với ∀ x ∈ D.
Do đó, hàm số đã cho nghịch biến trên các khoảng (– ∞; 0) và (0 ; +∞).
+ Giới hạn:
![]()
Suy ra: x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số
y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên:
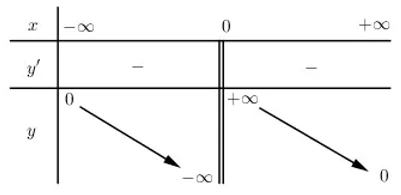
- Đồ thị:
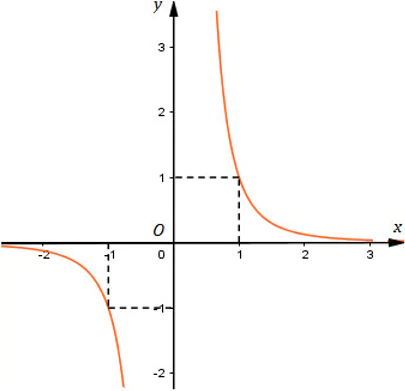
Kiến thức áp dụng
| y = xα; α > 0 | y = xα; α < 0 |
| 1. Tập khảo sát: (0; +∞) 2. Sự biến thiên y' = α.xα – 1 > 0; ∀x > 0 Giới hạn đặc biệt
Tiệm cận: Không có + Đồ thị hàm số luôn đi qua điểm (1 ; 1) | 1. Tập khảo sát: (0; +∞) 2. Sự biến thiên y' = α.xα – 1 < 0; ∀x > 0 Giới hạn đặc biệt
Tiệm cận: Trục Ox là tiệm cận ngang Trục Oy là tiệm cận đứng + Đồ thị hàm số luôn đi qua điểm (1 ; 1) |
Bài 4 trang 61 SGK
Hãy so sánh các số sau với 1:
a) (4,1)2,7;
b) (0,2)0,3;
c) (0,7)3,2;
d) (√3)0,4.
Lời giải:
a)
Cách 1. Ta có: 2,7 > 0 nên hàm y = x2,7 luôn đồng biến trên (0 ; +∞).
Vì 4,1 > 1 ⇒ (4,1)2,7 > 12,7 = 1.
Cách 2. Ta có 4,1 > 1 và 2,7 > 0 nên ta có :
(4,1)2,7 > (4,1)0 hay (4,1)2,7 > 1
b) Ta có: 0,3 > 0 nên hàm số y = x0,3 đồng biến trên (0 ; +∞).
Vì 0,2 < 1 ⇒ 0,20,3 < 10,3 = 1.
c) Ta có: 3,2 > 0 nên hàm số y = x3,2 đồng biến trên (0 ; +∞)
Vì 0,7 < 1 ⇒ 0,73,2 < 13,2 = 1.
d) Ta có: 0,4 > 0 nên hàm số y = x0,4 đồng biến trên (0 ; +∞)
Vì √3 > 1 ⇒ (√3)0,4 > 10,4= 1.
Kiến thức áp dụng
| Hàm số y = xα có y' = α.xα – 1 > 0 với α > 0 và x > 0 ⇒ Hàm số luôn đồng biến với > 0 và x > 0 Hay: Với α > 0, nếu x1 < x2 thì x1α < x2α Với mọi α > 0 ta có : 1α = 1 |
Bài 5 trang 61 SGK
Hãy so sánh các cặp số sau:
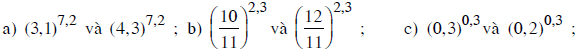
Lời giải:
Hàm số y = xα luôn đồng biến trên (0 ; +∞) với α > 0
a) Ta có: 7,2 > 0
Vì 3,1 < 4,3 nên (3,1)7,2 < (4,3)7,2.
b) Ta có: 2,3 > 0
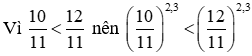
c) Ta có: 0,3 > 0
Vì 0,3 > 0,2 nên (0,3)0,3 > (0,2)0,3.
Kiến thức áp dụng
| Hàm số y = xα có y' = α.xα – 1 > 0 với α > 0 và x > 0 ⇒ Hàm số luôn đồng biến với > 0 và x > 0 Hay: Với α > 0, nếu x1 < x2 thì x1α < x2α |
















Bình Luận
Để Lại Bình Luận Của Bạn