Nội Dung Chính
Câu hỏi 1 trang 139 SGK
Thế nào là căn bậc hai của số thực dương a?
Lời giải:
Căn bậc hai của một số thực dương a là một số thực b sao cho b2 = a.
Bài 1 trang 140 SGK
Tìm các căn bậc hai phức của các số sau: -7; -8; -12; -20; -121
Lời giải:
Căn bậc hai của -7 là ±i√7 vì (±i√7)2 = -7
Căn bậc hai của -8 là ±2√2i vì (±2√2i)2 = -8
Căn bậc hai của -12 là ±2√3i vì (±2√3i)2 = -12
Căn bậc hai của -20 là ±2√5i vì (±2√5i)2 = -20
Căn bậc hai của -121 là ±11i vì (±11i)2 = -121
Kiến thức áp dụng
| Căn bậc hai của số thực a âm là |
Bài 2 trang 140 SGK
Giải các phương trình sau trên tập hợp số phức:
a) -3z2 + 2z – 1 = 0
b) 7z2 + 3z + 2 = 0
c) 5z2 – 7z + 11 = 0
Lời giải:
a) Phương trình -3z2 + 2z – 1 = 0
có Δ' = 12 – 3 = -2
⇒ Phương trình có hai nghiệm ![]()
b) Phương trình 7z2 + 3z + 2 = 0
có Δ = 32 – 4.7.2 = -47 < 0
⇒ Phương trình có hai nghiệm ![]()
c) Phương trình 5z2 – 7z + 11 = 0
có Δ = 72 – 4.5.11 = -171 < 0
⇒ Phương trình có hai nghiệm ![]()
Kiến thức áp dụng
| Phương trình bậc hai ax2 + bx + c = 0 có Δ = b2 – 4ac + Nếu Δ > 0, phương trình có hai nghiệm thực phân biệt: + Nếu Δ = 0, phương trình có nghiệm kép + Nếu Δ < 0, phương trình có hai nghiệm ảo phân biệt |
Bài 3 trang 140 SGK
Giải các phương trình sau trên tập hợp số phức:
a) z4 + z2 – 6 = 0
b) z4 + 7z2 + 10 = 0
Lời giải:
a) z4 + z2 – 6 = 0
⇔ z4 – 2z2 + 3z2 – 6 = 0
⇔ z2 .(z2 – 2)+ 3. (z2 – 2) = 0
⇔ (z2 – 2)(z2 + 3) = 0
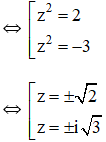
Vậy phương trình có tập nghiệm ![]()
b) z4 + 7z2 + 10 = 0
⇔ z4 + 5z2 + 2z2 + 10 = 0
⇔ z2 (z2 + 5) + 2.(z2 + 5) = 0
⇔ (z2 + 2)(z2 + 5) = 0
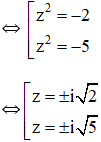
Vậy phương trình có tập nghiệm ![]()
Bài 4 trang 140 SGK
Cho a, b, c ∈ ℝ, a ≠ 0, z1, z2 là hai nghiệm của phương trình az2 + bz + c = 0.
Hãy tính z1 + z2 và z1.z2 theo hệ số a, b, c.
Lời giải:
Cách 1:
Phương trình az2 + bz + c = 0 có Δ = b2 – 4ac
+ TH1: Δ < 0, phương trình có hai nghiệm phức 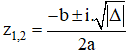
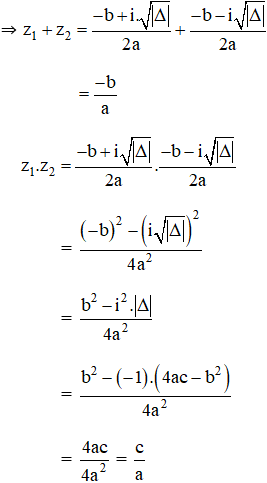
+ TH2: Δ ≥ 0, theo định lý Vi-et ta có:
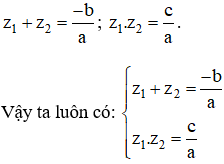
Cách 2:
Vì z1; z2 là hai nghiệm của phương trình az2 + bz + c = 0 nên ta có:
a.z12 + bz1 + c = 0 (1)
az22 + bz2 + c = 0 (2).
+ Trừ hai vế tương ứng của (1) cho (2) ta được:
a.(z12 – z22) + b(z1 – z2) = 0
⇔ a.(z1 – z2)(z1 + z2) + b.(z1 – z2) = 0
⇔ a.(z1 + z2) + b = 0
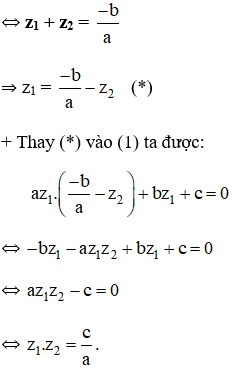
Bài 5 trang 140 SGK
Cho z = a + bi là một số phức. Hãy tìm một phương trình bậc hai với hệ số thực nhận z và ![]()
Lời giải:

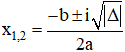

















Bình Luận
Để Lại Bình Luận Của Bạn