Nội Dung Chính
Câu hỏi 1 trang 114 SGK
Tính diện tích hình thang vuông được giới hạn các đường thẳng y = -2x – 1, y = 0, x = 1 và x = 5.
So sánh với diện tích hình thang vuông trong câu hỏi 1 bài 2.
Lời giải:
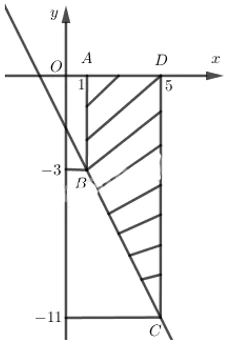
Gọi A(1; 0), D(5; 0)
B là giao điểm của đường thẳng x = 1 với đường thẳng y = -2x – 1 thì B(1; -3)
C là giao điểm của đường thẳng x = 5 với đường thẳng y = -2x − 1 thì C(5; -11)
Diện tích hình thang SABCD = ![]()
Diện tích hình thang này bằng diện tích hình thang vuông trong hoạt động 1 bài 2.
Câu hỏi 2 trang 117 SGK
Hãy nhắc lại công thức tính thể tích khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h.
Lời giải:
Công thức tính thể tích lăng trụ có diện tích đáy là B và chiều cao là h là:
V = B.h.
Câu hỏi 3 trang 119 SGK
Nhắc lại khái niệm mặt tròn xoay và khối tròn xoay trong hình học.
Lời giải:
- Khái niệm mặt tròn xoay: Trong không gian cho mặt phẳng (P) chứa đường thẳng Δ và một đường C. Khi quay mặt phẳng (P) quanh Δ một góc 360o thì mỗi điểm M trên đường C vạch ra một đường tròn có tâm O thuộc Δ và nằm trên mặt phẳng vuông góc với Δ. Như vậy khi quay mặt phẳng (P) quanh đường thẳng Δ thì đường C sẽ tao nên một hình được goi là mặt tròn xoay.
Đường C được gọi là đường sinh của mặt tròn xoay đó. Đường thẳng Δ được gọi là trục của mặt tròn xoay.
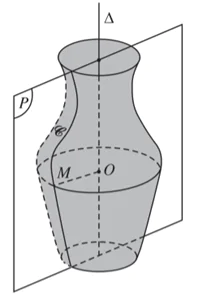
- Khái niệm khối tròn xoay: Khối tròn xoay là khối hình học được tạo thành khi quay một hình phẳng quanh một đường thẳng cố định (trục quay) của hình.

Bài 1 trang 121 SGK
Tính diện tích hình phẳng giới hạn bởi các đường:
a) y = x2; y = x + 2
b) y =|lnx|; y = 1
c) y = (x – 6)2; y = 6x – x2
Lời giải:
a) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
x2 = x + 2 ⇔ x2 – x – 2 = 0 ⇔ ![]()
Vậy diện tích cần tìm là:
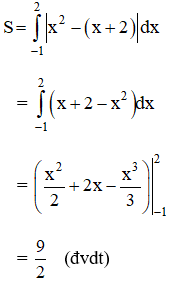
b) Hoành độ giao điểm hai đồ thị là nghiệm của pt:
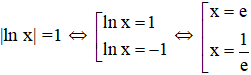
Vậy diện tích cần tìm là:
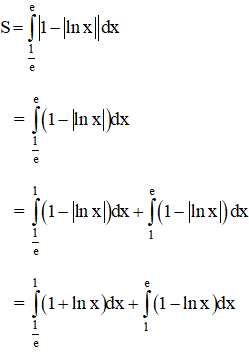
(Vì lnx > 0 khi 1 < x < e và lnx < 0 khi ![]() ).
).
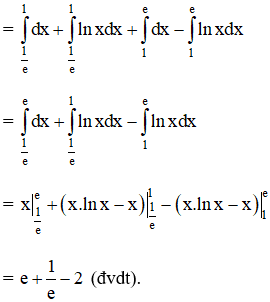
c) Hoành độ giao điểm của hai đồ thị là nghiệm của pt:
(x – 6)2 = 6x – x2
⇔ (x – 6)2 + x2 – 6x = 0
⇔ (x – 6). (x – 6+ x) = 0
⇔ (x – 6)(2x – 6) = 0
⇔ x = 3 hoặc x = 6
Vậy diện tích cần tìm là:
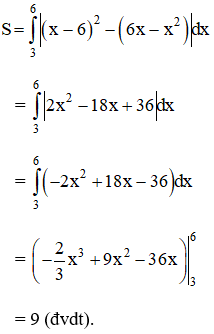
Kiến thức áp dụng
| + Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x); y = g(x) và hai đường thẳng x = a; x = b là:
|
Bài 2 trang 121 SGK
Tính diện tích hình phẳng giới hạn bởi đường cong y = x2 + 1 tiếp tuyến với đường này tại điểm M(2 ; 5) và trục Oy.
Lời giải:
Xét hàm số y = x2 + 1 có đạo hàm y’ = 2x
Phương trình tiếp tuyến với đường cong y = x2 + 1 tại điểm M(2 ; 5) là:
y = y’(2).(x – 2) + 5 ⇔ y = 4(x – 2) + 5 hay y = 4x – 3
Phương trình hoành độ giao điểm của đường cong và tiếp tuyến là :
x2 + 1 = 4x – 3 ⇔ x2 – 4x + 4 = 0 ⇔ x= 2
Vậy diện tích hình giới hạn bởi y = x2 + 1; tiếp tuyến y = 4x – 3 và trục Oy (x = 0) là:
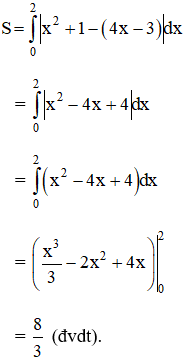
Kiến thức áp dụng
| + Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x); y = g(x) và hai đường thẳng x = a; x = b là:
+ Phương trình tiếp tuyến của đường cong y = f(x) tại điểm M(x0 ; y0) là: y = f’(x0).( x – x0) + y0 |
Bài 3 trang 121 SGK
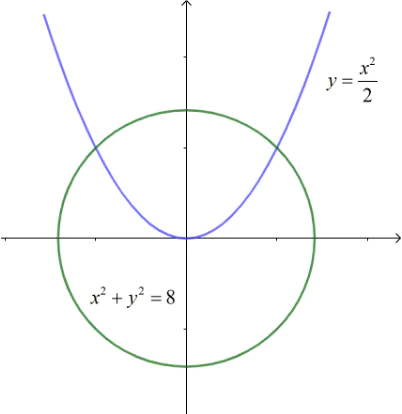
Parabol ![]() chia hình tròn có tâm tại gốc tọa độ, bán kính 2√2 thành hai phần. Tìm tỉ số diện tích của chúng.
chia hình tròn có tâm tại gốc tọa độ, bán kính 2√2 thành hai phần. Tìm tỉ số diện tích của chúng.
Lời giải:
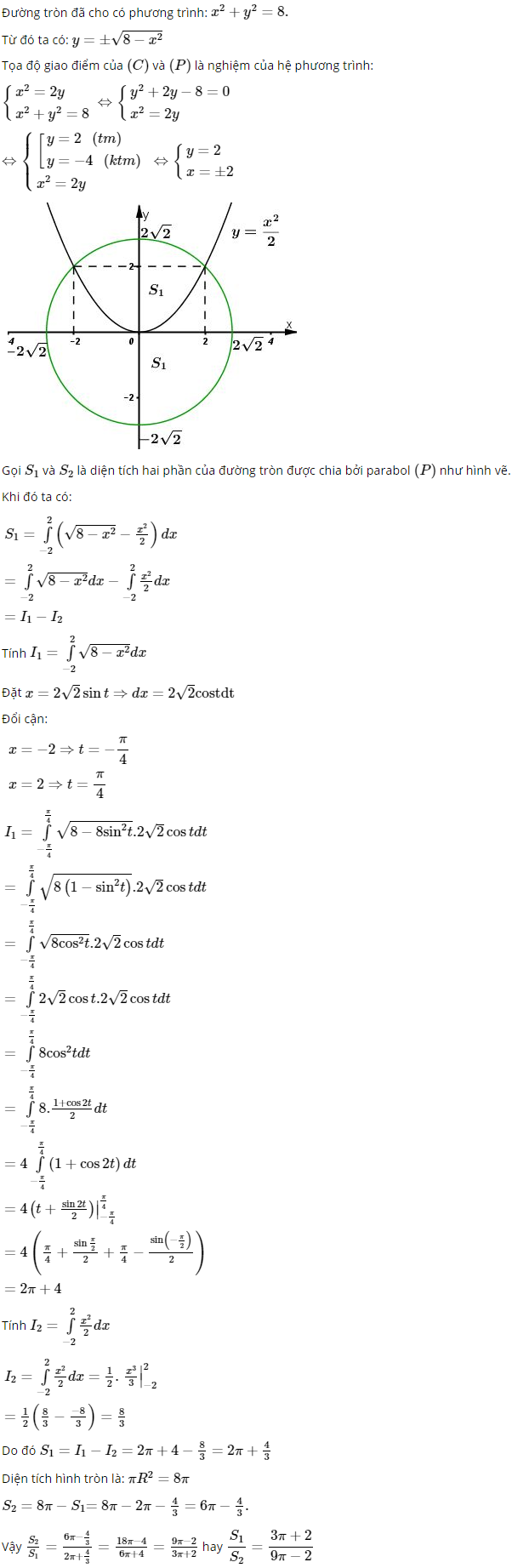
Bài 4 trang 121 SGK
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục Ox.
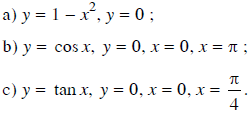
Lời giải:
a) Hoành độ giao điểm là nghiệm của phương trình :
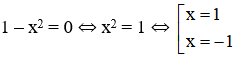
Vậy thể tích khối tròn xoay cần tính là:
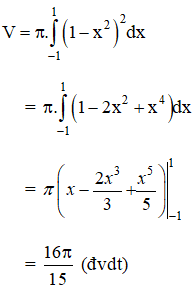
b) Thể tích khối tròn xoay cần tính:
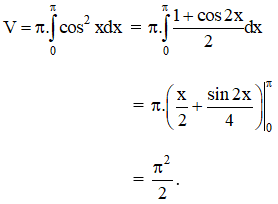
c) Thể tích khối tròn xoay cần tính:
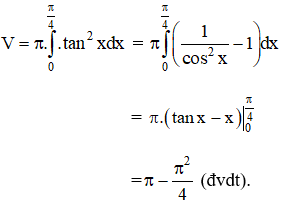
Kiến thức áp dụng
| Thể tích khối tròn xoay do hình phẳng giới hạn bởi đồ thị y = f(x), trục Ox, đường thẳng x = a; x = b quay quanh trục Ox tạo thành là:
|
Bài 5 trang 121 SGK
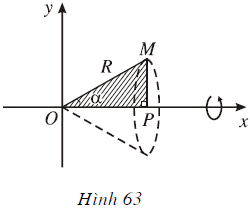
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt
![]()
Gọi V là khối tròn xoay thu được khi quay tam giác đó quanh trục Ox (H.63).
a) Tính thể tích của V theo α và R.
b) Tìm α sao cho thể tích V lớn nhất.
Lời giải:
a) Ta có: OP = OM.cosα = R. cosα
Phương trình đường thẳng OM đi qua O nên có dạng: y = k.x
OM tạo với trục hoành Ox 1 góc
⇒ Hệ số góc k = tanα
⇒ OM: y = x.tanα
Vậy khối tròn xoay được tạo bởi hình phẳng giới hạn bởi đường thẳng y = x.tanα; y = 0; x = 0; x = R.cosα quay quanh trục Ox
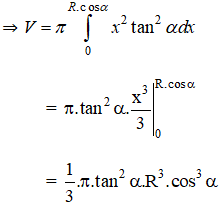
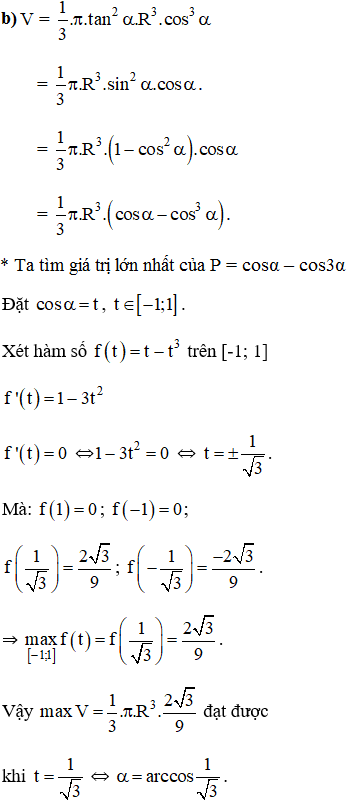
Kiến thức áp dụng
| + Đường thẳng đi qua gốc tọa độ có dạng: y = kx. Trong đó, k là hệ số góc và k = tan α với α là góc tạo bởi đưởng thẳng và tia Ox. + Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số y = f(x); trục Ox và hai đường thẳng x = a và x = b (a < b) là:
|
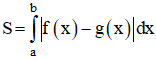
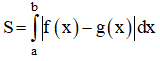
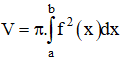
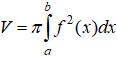
















Bình Luận
Để Lại Bình Luận Của Bạn