Nội Dung Chính
Bài 1 trang 126 SGK
a) Phát biểu định nghĩa nguyên hàm của hàm số f(x) trên một khoảng.
b) Nêu phương pháp tính nguyên hàm từng phần. Cho ví dụ minh họa.
Lời giải:
a) Cho hàm số f(x) xác định trên K.
Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K
⇔ F’(x) = f(x) ∀ x ∈ K.
b)
+ Phương pháp nguyên hàm từng phần:
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:
∫u(x).v’(x)dx = u(x).v(x) – ∫v(x).u’(x)dx
Hay viết gọn: ∫udv = uv – ∫vdv.
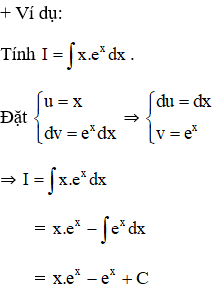
Bài 2 trang 126 SGK
a) Phát biểu định nghĩa tích phân của hàm số f(x) trên một đoạn.
b) Nêu các tính chất của tích phân. Cho ví dụ minh họa.
Lời giải:
a) Cho hàm số y = f(x) liên tục trên [a; b].
F(x) là một nguyên hàm của f(x) trên [a; b].
Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x)
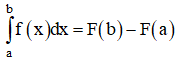
b) Các tính chất:
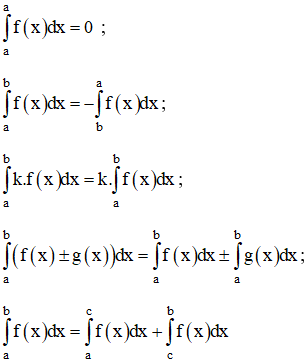
Bài 3 trang 126 SGK
Tìm nguyên hàm của các hàm số sau:
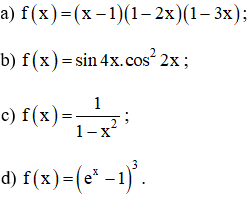
Lời giải:
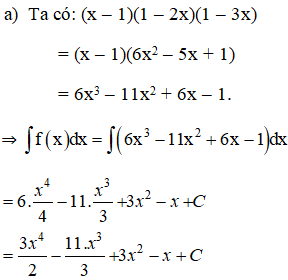
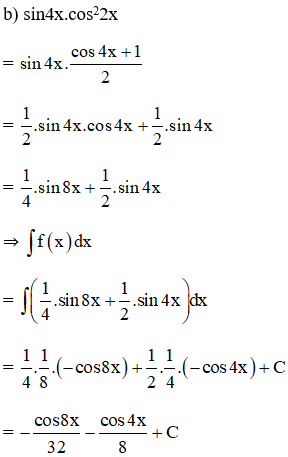
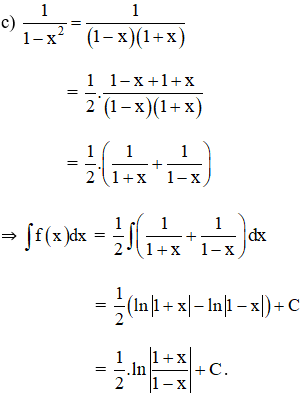
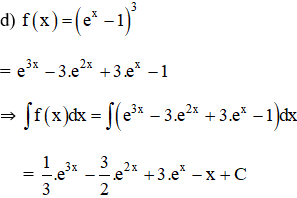
Kiến thức áp dụng
| Một số nguyên hàm thường dùng:
|
Bài 4 trang 126 SGK
Tính:
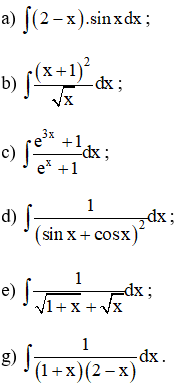
Lời giải:

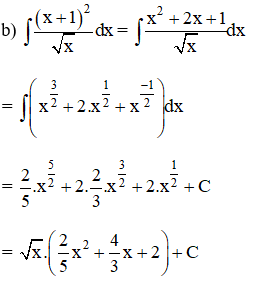
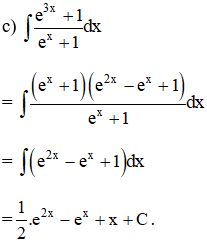
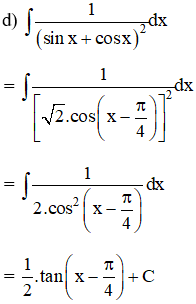
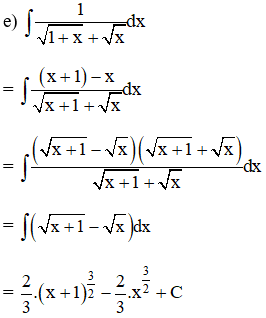
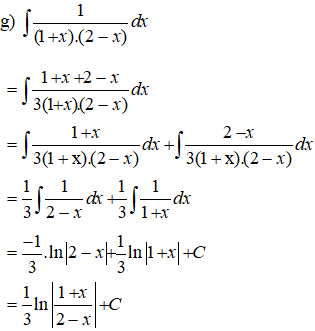
Kiến thức áp dụng
| + Phương pháp nguyên hàm từng phần: Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì: ∫u(x).v’(x)dx = u(x).v(x) – ∫v(x).u’(x)dx Hay viết gọn: ∫udv = uv – ∫vdv.
|
Bài 5 trang 127 SGK
Tính:
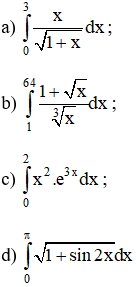
Lời giải:
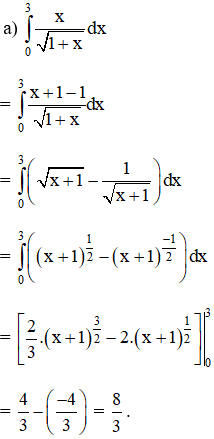
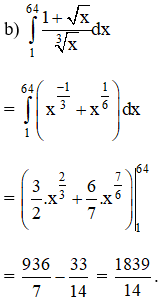
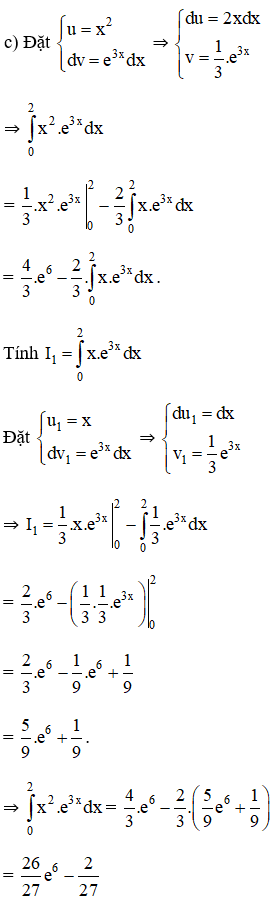
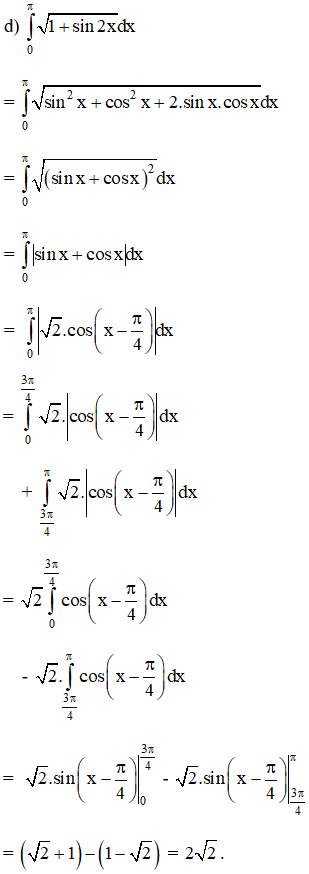
Bài 6 trang 127 SGK
Tính:
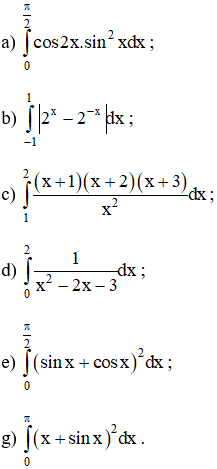
Lời giải:
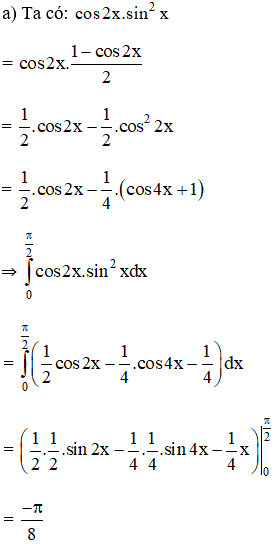
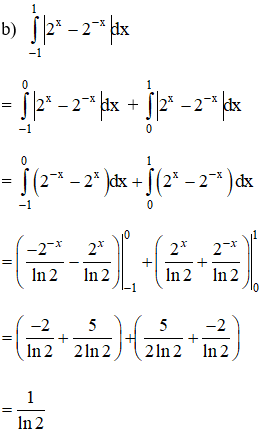
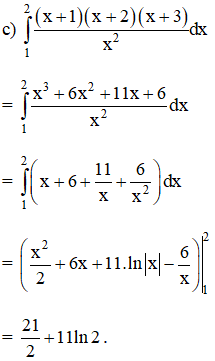
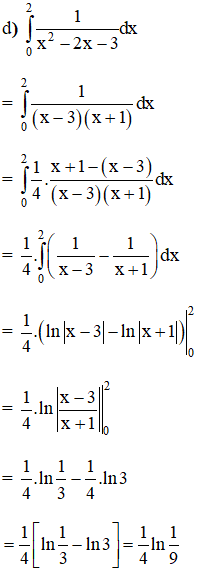
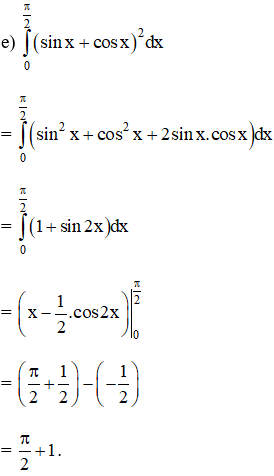
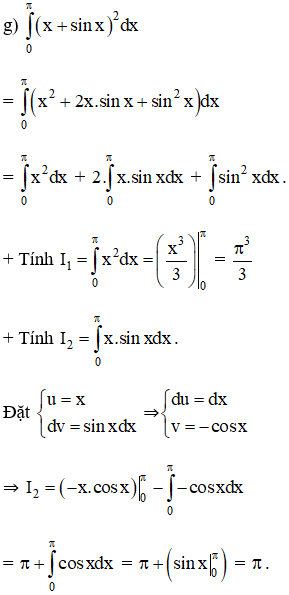
Bài 7 trang 127 SGK
Xét hình phẳng D giới hạn bởi ![]() và y = 2(1 - x)
và y = 2(1 - x)
a) Tính diện tích hình D.
b) Quay hình D xung quanh trục Ox. Tính thể tích khối tròn xoay được tạo thành.
Lời giải:
a) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
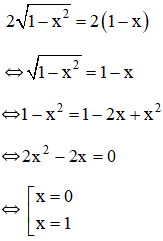
Vậy diện tích hình D là:
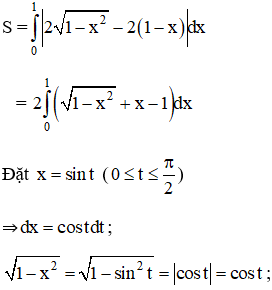
Đổi biến:
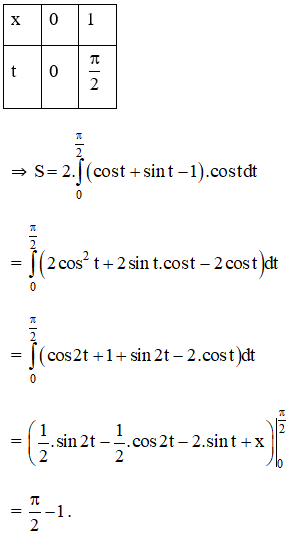
b)
+ Thể tích khối tròn xoay do hình phẳng giới hạn bởi 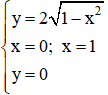 quay quanh trục Ox tạo thành là:
quay quanh trục Ox tạo thành là:
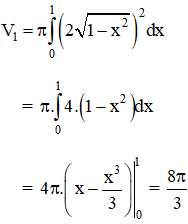
+ Thể tích khối tròn xoay do hình phẳng giới hạn bởi 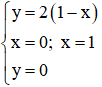
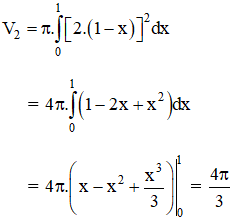
+ Thể tích khối tròn xoay do hình phẳng D quay quanh trục Ox là:
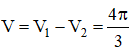
Bài tập trắc nghiệm
Bài 1 trang 127 SGK
Tính ![]() , kết quả là:
, kết quả là:
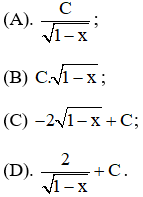
Lời giải:
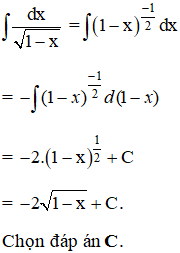
Bài 2 trang 128 SGK
Tính ![]() , kết quả sai là:
, kết quả sai là:
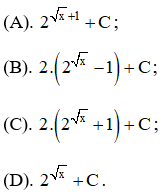
Lời giải:
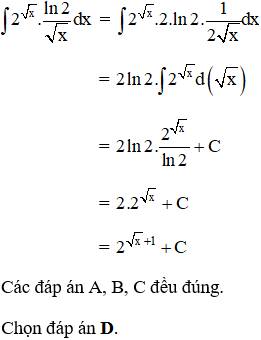
Bài 3 trang 128 SGK
Tích phân 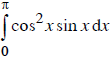 bằng:
bằng:
![]()
Lời giải:
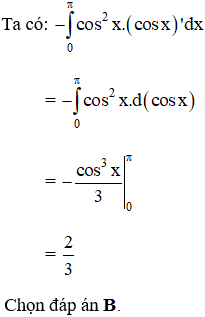
Bài 4 trang 128 SGK
Cho hai tích phân 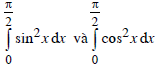 . Hãy chỉ ra khẳng định đúng:
. Hãy chỉ ra khẳng định đúng:

Lời giải:
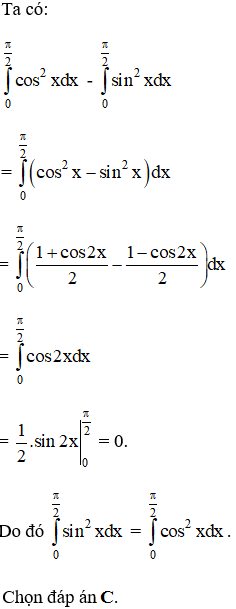
Bài 5 trang 128 SGK
Diện tích hình phẳng giới hạn bởi các đường cong
a) y = x3 và y = x5 bằng:
A. 0 B. −4 C. 1/6 D. 2
b) y = x + sinx và y = x (0≤ x ≤2π) bằng:
A. −4 B. 4 C. 0 D. 1
Lời giải:
a) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
x3 = x5 ⇔ x3(x2 – 1) = 0 ⇔ 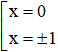
Vậy diện tích cần tính:
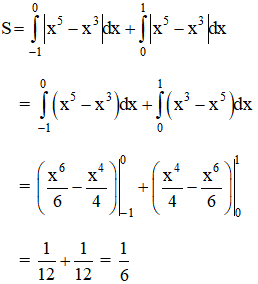
Chọn đáp án C.
b) Hoành độ giao điểm là nghiệm của phương trình:
x + sin x = x ⇔ sin x = 0 ⇔ 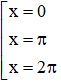
Diện tích cần tính:
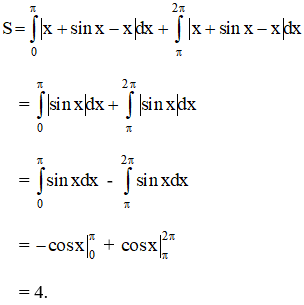
Chọn đáp án B.
Bài 6 trang 128 SGK
Cho hình phẳng giới hạn bởi các đường thẳng y =√x và y = x quay xung quanh trục Ox. Thể tích của khối tròn xoay tại thành bằng:
A. 0 B. –π
C. π D. π/6
Lời giải:
Hoành độ giao điểm hai đồ thị là nghiệm của phương trình:
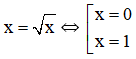
Thể tích cần tính:
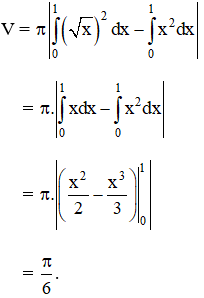
Chọn đáp án D.
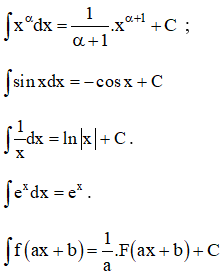
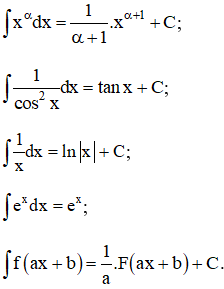

















Bình Luận
Để Lại Bình Luận Của Bạn