Nội Dung Chính
Câu hỏi và bài tập
Bài 1 trang 7 SGK
Xét chiều biến thiên của các hàm số sau:

Lời giải:
a. Hàm số y = 2x3 + 3x2 + 1 xác định trên R.
Ta có: y' = 6x2 + 6x = 0 = 6x (x + 1)
y' = 0 => x = 0 hoặc x = -1
Chiều biến thiên của hàm số được nêu trong bảng sau:
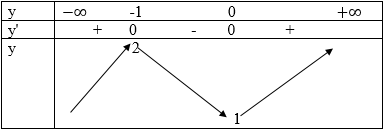
Vậy hàm số đồng biến trên mỗi khoảng (-∞; -1) và (0; +∞) nghịch biến trên (-1;0)
b. Tập xác định: R
Đạo hàm y’ = 3x2 – 4x + 1
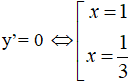
Bảng biến thiên:
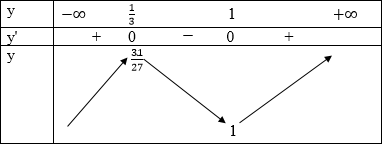
Vậy hàm số đồng biến trên mỗi khoảng (-∞; 1/3) và (1; +∞) nghịch biến trên ( 1/3; 1)
c. Tập xác định: R\{0}
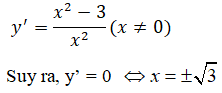
Bảng biến thiên:
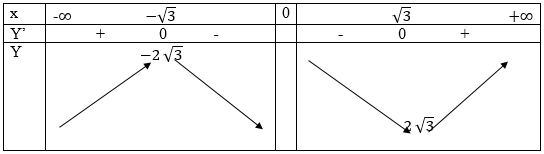
Vậy hàm số đồng biến trên mỗi khoảng (-∞,-√3) và (√3; +∞) hàm nghịch biến trên mỗi khoảng (-√3; 0) và (0; √3)
d. Tập xác định: D = R\ {0}
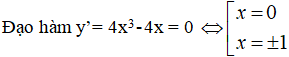
Vậy hàm số đồng biến trên mỗi khoảng (-∞; 0) và (0; +∞)
e. Tập xác định: R
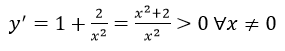
Bảng biến thiên:
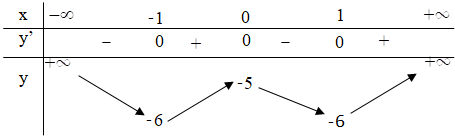
Hàm số đồng biến trên khoảng (-1; 0) và (1; +∞)
Hàm số nghịch biến trên khoảng (-∞; -1) và (0; 1).
f. Hàm số ![]()
Tập xác định : D = [-2; 2]
Đạo hàm: 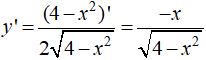
Bảng biến thiên:
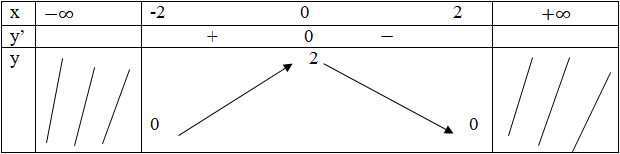
Vậy hàm số đồng biến trên [-2; 0] và nghịch biến trên [0; 2] (có thể trả lời: hàm số đồng biến trên (-2; 0) và nghịch biến trên (0; 2).
Bài 2 trang 7 SGK
Chứng minh rằng:
a) Hàm số ![]() đồng biến trên mỗi khoảng xác định của nó;
đồng biến trên mỗi khoảng xác định của nó;
b) Hàm số ![]() nghịch biến trên mỗi khoảng xác định của nó.
nghịch biến trên mỗi khoảng xác định của nó.
a. Hàm số xác định trên R \ {-2}
Ta có đạo hàm:
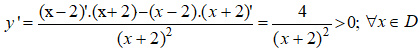
Nên hàm số đồng biến trên mỗi khoảng (-∞; -2) và (-2 ; +∞)
b. Hàm số xác định trên R \ {-1}
Đạo hàm:
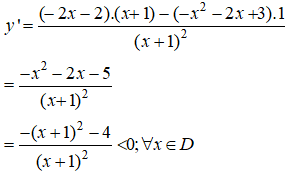
Nên hàm số nghịch biến trên mỗi khoảng ( -∞; -1) và (-1; +∞)
Bài 3 trang 8 SGK
Chứng minh rằng các hàm số sau đây đồng biến trên R:
a)f(x) = x3 – 6x2 + 17x + 4 = 0;
b) f(x) = x3 + x – cosx – 4
Lời giải:
a. Hàm số f(x) = x3 – 6x2 + 17x + 4 = 0 xác định trên R.
Ta có f' (x) = 3x2 – 12x + 17 = 3(x –2)2 + 5 > 0 ∀x ∈ R.
Nên hàm số đồng biến trên R.
b. Hàm số f(x) xác định trên R.
Và f' (x) = 3x2 + 1 + sinx > 0 ∀x ∈ R
Vì: x2 ≥ 0; 1 + sinx ≥ 0; 3x2 + 1 + sinx = 0 vô nghiệm nên hàm số đồng biến trên R.
Bài 4 trang 8 SGK
Với giá trị nào của a, hàm số y = ax – x3 nghịch biến trên R?
Lời giải:
Hàm số xác định trên R, y' = a – 3x2
Cách 1. Nếu a < 0 => y’ < 0 ∀x ∈ R => hàm số nghịch biến trên R.
Nếu a = 0 => y’ = -3x2 ≤ 0, ∀x ∈ R, y' = 0 ⇔ x = 0
Vậy hàm số nghịch biến trên R.
Nếu a > 0 thì y' = 0
![]()
Bảng biến thiên:
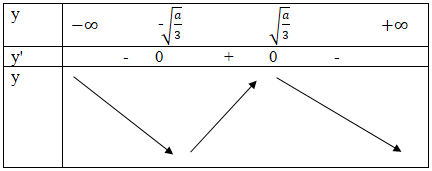
Cách 2. Hàm số nghịch biến trên R, điều kiện y' ≤ 0, ∀x ∈ R, y'= 0 chỉ tại một số hữu hạn điểm.
Ta có: y' ≤ 0 ⇔ a – 3x2 ≤ 0, ∀x ⇔ 3x2 ≥ a2 ∀x ∈ R
⇔ a ≤ min(3x2 ), mà 3x2 ≥0 ∀x ∈ R
⇔ a ≤ min(3x2), mà 3x2 ≥ 0 ∀x ∈ R
![]()
Kết luận: với a ≤ 0 thì y = ax – 3x3 nghịch biến trên R.
Bài 5 trang 8 SGK
Tìm các giá trị của tham số a để hàm số
![]()
đồng biến trên R.
Lời giải:
Tập xác định: D = R.
Đạo hàm: f’ = x2 + 2ax + 4 có ![]()
Để hàm số đã cho đồng biến trên R khi và chỉ khi ![]()
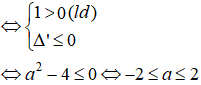
Kết luận: Vậy để hàm số đã cho đồng biến trên R khi và chỉ khi -2 ≤ a ≤ 2
Chú ý: Để tam thức bậc hai f(x)= ax2 + bx + c ≤ 0; ∀ x khi và chỉ khi: 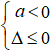
Luyện tập
Bài 6 trang 8 SGK
Xét chiều biến thiên của các hàm số sau:
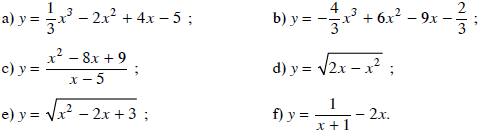
Lời giải:
![]()
TXĐ: D = R
y′ = x2 − 4x + 4 = (x − 2)2 ≥ 0, ∀x ∈ R
Dấu bằng chỉ xảy ra khi x = 2
Vậy hàm số đồng biến trên R.
![]()
TXĐ: D = R
y′ = −4x2 + 12x − 9
= −(4x2 −12x + 9)
= −(2x − 3)2 ≤ 0, ∀x ∈ R
Dấu bằng chỉ xảy ra khi x = ![]() .
.
Vậy hàm số nghịch biến trên R.
![]()
TXĐ: D = R∖{5}
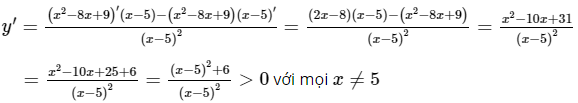
Vậy hàm số đồng biến trên mỗi khoảng (−∞; 5) và (5; +∞).
![]()
Hàm số xác định khi và chỉ khi 2x − x2 ≥ 0 ⇔ 0 ≤ x ≤ 2.
TXĐ: D = [0; 2]
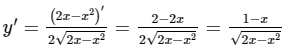
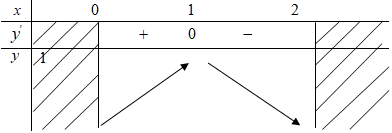
y′ = 0 ⇔ x = 1 (y = 1)
Hàm số đồng biến trên khoảng (0; 1) và nghịch biến trên khoảng (1; 2).
Bảng biến thiên:
![]()
TXĐ: D = R
(vì x2 − 2x + 3 = (x − 1)2 + 2 > 0, ∀x ∈ R)
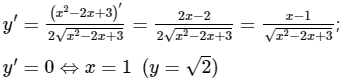
Bảng biến thiên
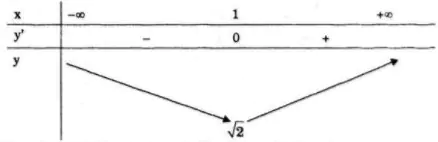
Hàm số nghịch biến trên khoảng (−∞; 1) và đồng biến trên khoảng (1; +∞).
![]()
TXĐ: D = R∖{−1}
![]()
Hàm số nghịch biến trên mỗi khoảng (−∞; −1) và (−1; +∞) .
Bài 7 trang 8 SGK
Chứng minh rằng hàm số: f(x) = cos2x − 2x + 3 nghịch biến trên R.
Lời giải:
TXĐ: D = R
f′(x) = -2sin2x − 2
= -2(sin2x + 1)
Do -1 ≤ sin2x ≤ 1
⇒ sin2x + 1 ≥ 0, ∀x
⇒ f′(x) = -2(sin2x + 1) ≤ 0, ∀x
f′(x) = 0 ⇔ sin2x = -1
⇔ 2x = ![]() + k2π, k ∈ Z
+ k2π, k ∈ Z
⇔ x = ![]() + kπ, k ∈ Z
+ kπ, k ∈ Z
Do đó hàm số nghịch biến trên mỗi đoạn [![]()
![]() + (k + 1)π]
+ (k + 1)π]
Vậy hàm số nghịch biến trên R.
Bài 8 trang 8 SGK
Chứng minh các bất đẳng thức sau:
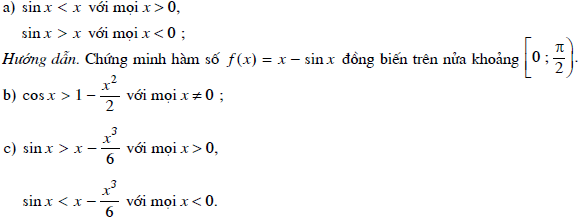
Lời giải:
a) sinx < x với mọi x > 0, sinx > x với mọi x < 0
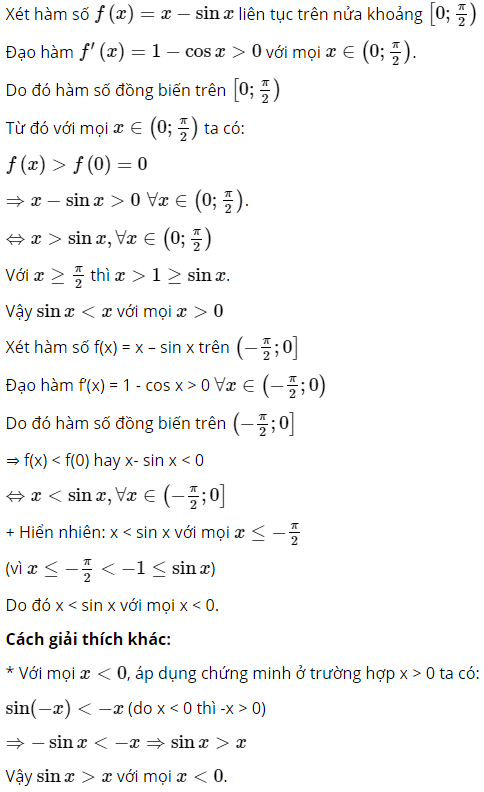

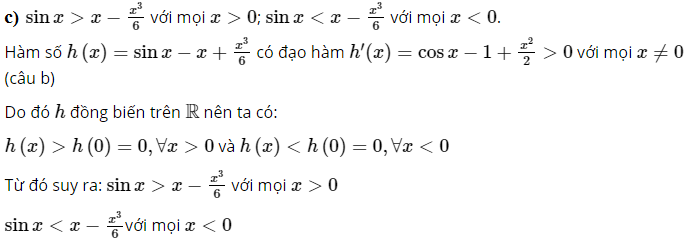
Bài 9 trang 9 SGK
Chứng minh rằng
![]()
Hướng dẫn
Chứng minh hàm số đồng biến trên nửa khoảng (0; ![]() ).
).
Lời giải:
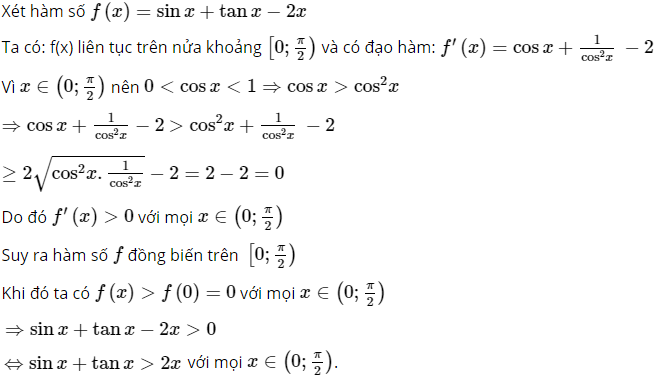
Bài 10 trang 9 SGK
Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức
![]()
(f(t) được tính bằng nghìn người).
a) Tính số dân của thị trấn vào năm 1980 và năm 1995.
b) Xem f là một hàm số xác định trên nửa khoảng [0; +∞). Tính f′ và xét chiều biến thiên của hàm số f trên nửa khoảng [0; +∞)
c) Đạo hàm của hàm số f biểu thị tốc độ tăng dân số của thị trấn ( tính bằng nghìn người/năm).
• Tính tốc độ tăng dân số vào năm 1990 và năm 2008 của thị trấn.
• Vào năm nào thì tốc độ gia tăng dân số là 0,125 nghìn người/năm?
Lời giải:
a)

b)
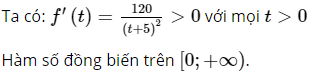
c)
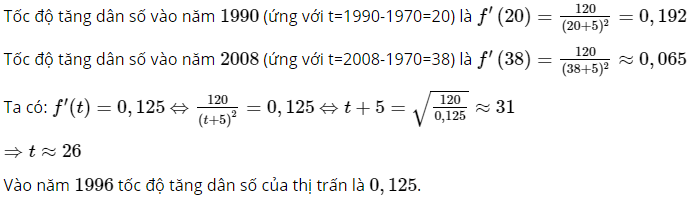

















Bình Luận
Để Lại Bình Luận Của Bạn