Bài 3. Dạng lượng giác của số phức và ứng dụng | Bài giải GIẢI TÍCH 12 (Nâng Cao) | CHƯƠNG IV - SỐ PHỨC - Lớp 12 - Sách Bài Giải

Câu hỏi và bài tập

Bài 27 trang 205 SGK

Hãy tìm dạng lượng giác của các số phức

a) z = r(cos⁡φ + isinφ) (r>0);

b) z = 1 + i√3.

Lời giải:

a) Ta có:

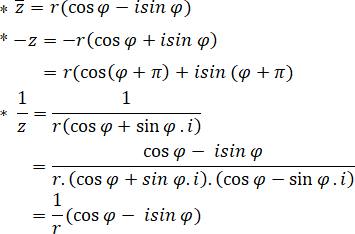
Kz là một số phức có modun là |Kz| = |K|. |z| = |K|.r, có acgumen là φ nếu K > 0, là φ+π nếu k < 0.

Vậy Kz = |K|.r(cos⁡φ + isinφ) nếu k > 0

Kz = |K|r. (cos⁡(φ + π) + isin (φ + π) nếu k < 0

b) Khi z = 1 + i√3

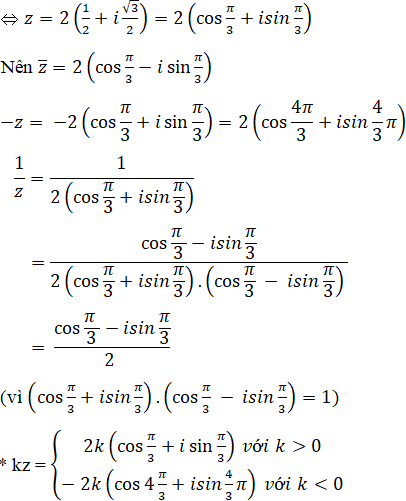
Bài 28 trang 205 SGK

Viết các số phức sau dưới dạng lượng giác:

a) 1 – i√3;  1+i;  (1 – i√3)(1 + i);  (1 – i√3)/(1 + i);

b) 2i(√3 – i);

c) 1/(2 + 2i);

d) z = sin⁡φ + cosφ (φ ∈ R).

Lời giải:

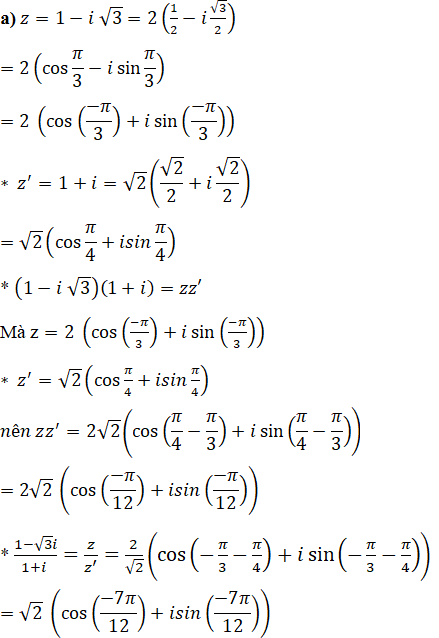
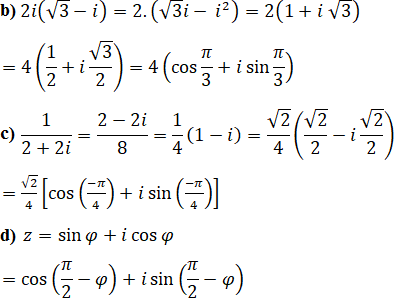
Bài 29 trang 206 SGK

Dùng công thức khai triển nhị thức Niu-tơn (1 + i)¹⁹ và công thức Moa-vrơ để tính:

Lời giải:

Theo nhị thức Nui-tơn ta có:

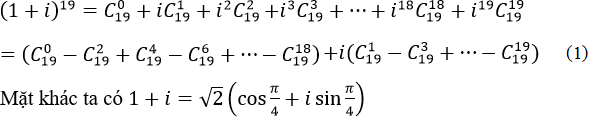
Nên công thức Moa-vrơ ta có:

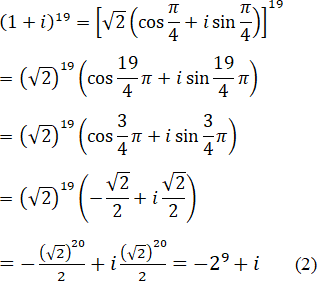
So sánh (1) và (2) ta có:

Bài 30 trang 206 SGK

Gọi M, M’ là các điểm trong mặt phẳng phức theo thứ tự biểu diễn các số z = 3 + i; z' = (3 – √3) + (1 + 3√3)i.

a) Tính z'/z.

b) Chứng minh rằng hiệu số acgumen của z’ với acguemn của z là một số đo của góc lượng giác (OM, OM’). Tính số đo đó.

Lời giải:

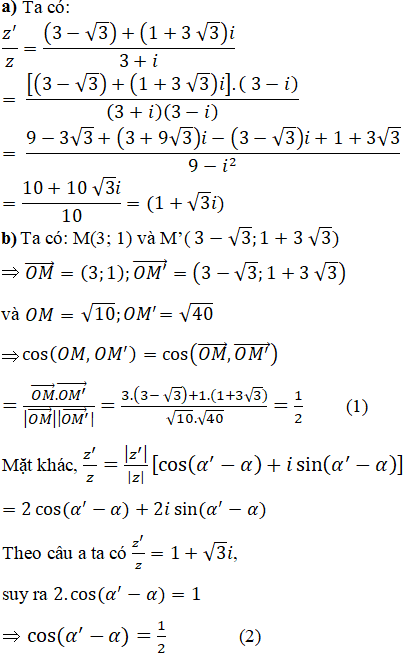
Từ (1) và (2) ta có: cos⁡(α' – α) = cos⁡(OM, OM') nên kí hiệu α' – α là một số đo của góc lượng giác (OM, OM’) và số đo là

Bài 31 trang 206 SGK

Cho các số phức

a) Chứng minh rằng z₀ = cos(π/12) + isin(π/12), z₁ = z₀ε, z₂ = z₀ε² là các nghiệm của phương trình z³ − w = 0;

b) Biểu diễn hình học các số phức z₀; z₁; z₂.

Lời giải:

a) Ta có: z₀ = cos(π/12) + isin(π/12)

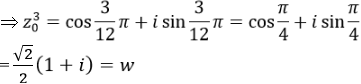
Vậy z₀³ – w = 0 hay z₀ là một nghiệm của phương trình: z³ − w = 0

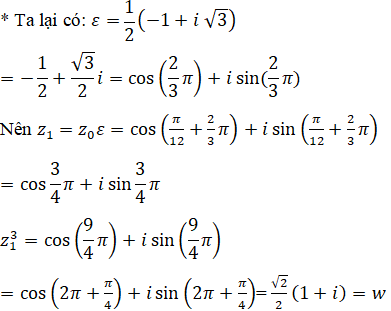
Vậy z₁³ – w = 0 hay z₁ là một nghiệm của phương trình: z³ − w = 0

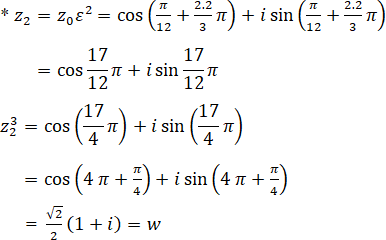
Vậy z₂³ – w = 0 hay z₂ là một nghiệm của phương trình: z³ − w = 0

b) Các điểm A, B, C lần lượt biểu diễn các số:

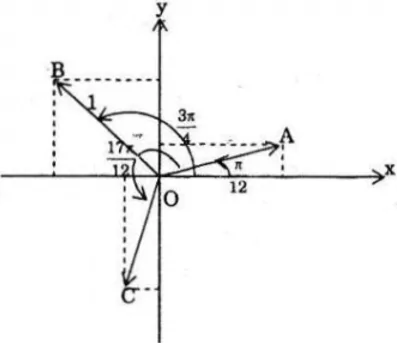
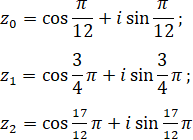
Nhận xét: ba điểm A, B, C tạo thành một tam giác đều.

Luyện tập

Bài 32 trang 207 SGK

Sử dụng công thức Moa-vrơ để tính sin⁡4α và cos⁡4α theo các lũy thừa sin⁡α và cos⁡α.

Lời giải:

Theo công thức Moa-vrơ ta có:

(cos⁡α + i sin⁡α)⁴ = cos⁡4α + i sin⁡4α

⇔ (cos⁴α – 6 sin²⁡α . cos²⁡α + sin⁴α) + 4(cos³⁡α sin⁡α – sin³⁡α.cos⁡α )i = cos⁡4α + i sin⁡4α

Bài 33 trang 207 SGK

Tính

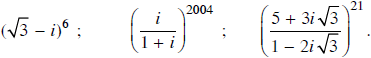
Lời giải:

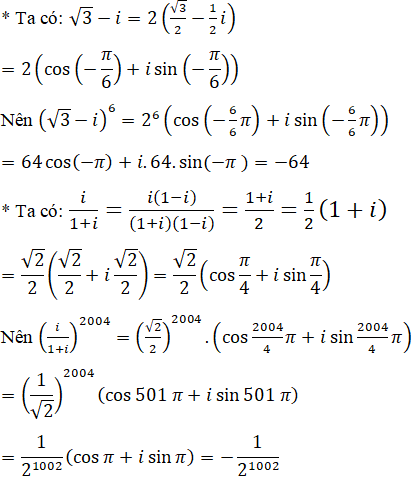
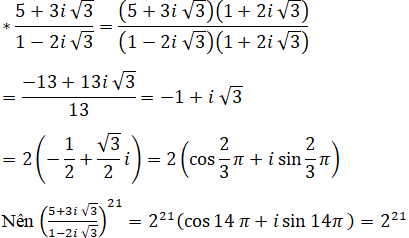
Bài 34 trang 207 SGK

Cho số phức

Tìm các số nguyên dương n để wⁿ là số thực. hỏi có số nguyên dương m nào để wm là số ảo?

Lời giải:

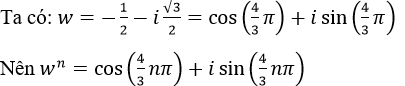
Để wⁿ là số thực thì

Để n ∈ N* thì k = 4 với t ∈ N*. Khi đó n = 3t, với t ∈ N*

Để w^m là số ảo thì

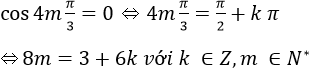
Vì phương trình này vô nghiệm, nên không tồn tại m để w^m là số ảo.

Bài 35 trang 207 SGK

Viết dạng lượng giác của số phức z và của các căn bậc hai của z cho mỗi mỗi trường hợp sau:

Lời giải:

Giả sử z = r(cos⁡α + isin⁡α)

a) Vì |z| = 3 ⇒ r = 3

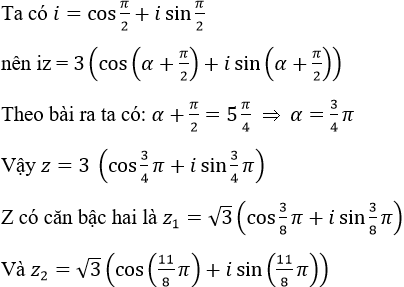
b) Vì |z| = 1/3 ⇒ r = 1/3

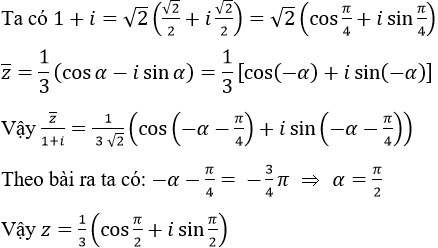
z có hai căn bậc hai là:

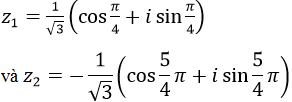
Bài 36 trang 207 SGK

Viết dạng lượng giác của các số phức:

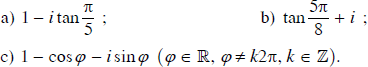
Lời giải: