Nội Dung Chính
Câu hỏi và bài tập
Bài 29 Trang 172 SGK
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = -1 và x = 1, biết rằng thiết diện vuông góc với trục Ox tại điểm có hoành độ x (-1 ≤ x < 1) là một hình vuông cạnh 2 √(1 – x2 ).
Lời giải:
Diện tích của thiết diện là:
![]()
Thể tích của vật thể cần tìm là:
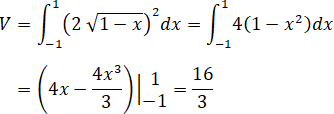
Bài 30 Trang 172 SGK
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 và x = π, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ (0 ≤ x ≤ π) là một tam giác đều cạnh 2 √(sinx).
Lời giải:
Diện tích thiết diện là:
![]()
Vậy thể tích của vật thể đã cho là:
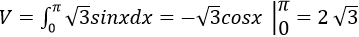
Bài 31 Trang 172 SGK
Cho hình phẳng A giới hạn bởi các đường y = 0; x = 4, y = √x – 1. Tính thể tích khối tròn xoay tạo thành khi quay quanh A trục hoành.
Lời giải:
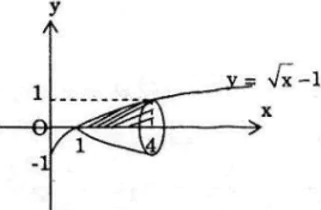
Giao điểm của đường y = √x – 1 và đường y = 0 có hoành độ giao điểm là x = 1, như vậy:
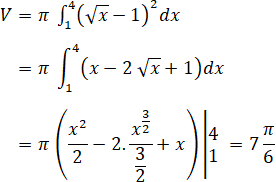
Bài 32 Trang 173 SGK
Cho hình phẳng B giới hạn bởi các đường x = 2/y, y = 1 và y = 4. Tính thể tích khối tròn xoay tạo thành khi quay hình B quanh trục tung.
Lời giải:
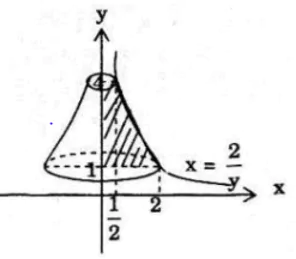
Thể tích vật cần tìm là:
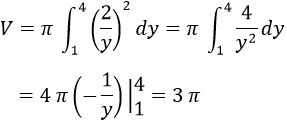
Bài 33 Trang 173 SGK
Cho hình phẳng B giới hạn bởi các đường x = √5 y2, x = 0, y = -1 và y = 1. Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung.
Lời giải:
Thể tích khối tròn xoay tạo thành:
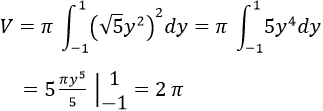
Luyện tập
Bài 34 Trang 174 SGK
Tính diện tích hình phẳng giới hạn bởi:
a) Đồ thị hai hàm số y = x, y = 1 và y = x2/4 trong miền x ≥ 0; y ≤ 1;
b) Đồ thị hai hàm số y = x4 – 4x2 + 4; y = x2, trục tung và đường thẳng x = 1;
c) Đồ thị các hàm số y = x2, y = 4x – 4 và y = -4x – 4.
Lời giải:
a) Cách 1.
Hoành độ giao điểm của đường thẳng y = x và y = 1 là x = 1
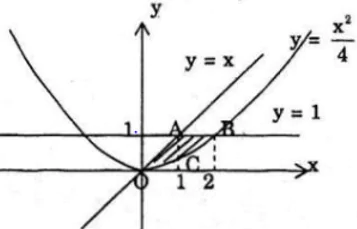
Hoành độ giao điểm của đường thẳng y = 1 và đường cong y = x2/4 trong miền x ≥ 0 là x = 2.
Diện tích hình phẳng cần tìm chính là tổng diện tích tam giác cong OAC và tam giác cong ACB.
Diện tích tam giác cong OAC là:
![]()
Diện tích tam giác cong ACB là:
![]()
Vậy diện tích hình phẳng cần tìm là: ![]()
Cách 2. Gọi hình phẳng đã cho là hình phẳng giới hạn bởi đường cong có phương trình x=2 √y,dường thẳng x = y và y = 0 và đường thẳng y = 1. Diện tích cần tìm là:
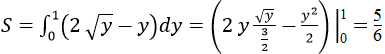
b) Diện tích hình phẳng cần tìm là:
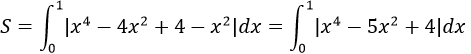
Vì x4 – 5x2 + 4 = (x2 – 1)(x2 – 4) > 0 ∀x ∈ [0; 1]
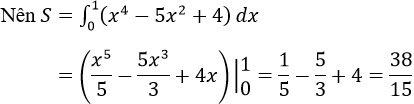
c) Ta thấy đường thẳng y = -4x – 4 và đường thẳng y = 4x – 4 lần lượt là hai tiếp tuyến của đồ thị hàm số y = x2 tại các tiếp điểm có hoành độ x = -2 và x = 2.
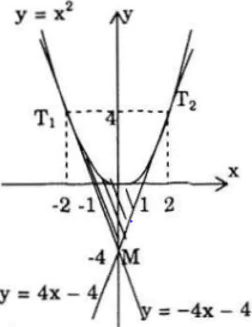
Do tính đối xứng qua Oy của parabol y = x2 nên diện tích hình phẳng cần tìm bằng 2 lần diện tích tam giác cong OMT2 và bằng:
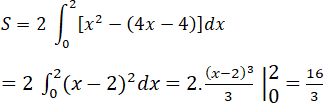
Bài 35 Trang 175 SGK
Tính diện tích hình phẳng giới hạn bởi:
a) Đồ thị hai hàm số y = x2 + 1 và y = 3 – x;
b) Các đường có Phương trình x = y3, y = 1, x = 8;
c) Đồ thị hai hàm số y = √x, y = 6 – x và trục hoành.
Lời giải:
a) Hoành độ giao điểm của hai đồi thị hàm số y = x2 + 1 và y = 3 – x là nghiệm của phương trình:
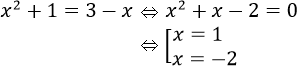
Vậy diện tích cần tìm là:
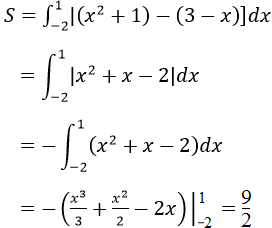
b) Tung độ giao điểm của đường cong x = y3 và đường thẳng x = 8 là nghiệm của phương trình y3 = 8 ⇔ y = 2. Vậy diện tích cần tìm là:
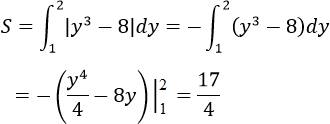
c) Ta có: y = √x ⇔ y2 = x (y ≥ 0); y = 6 – x ⇔ x = 6 – y
Tung độ giao điểm của hai đường thẳng x = y2; x = 6 – y là nghiệm của phương trình
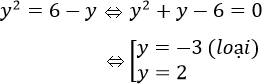
Vậy diện tích cần tìm:
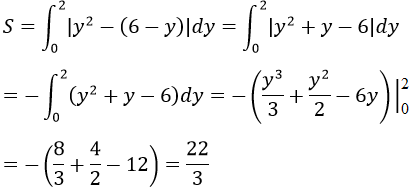
Bài 36 Trang 175 SGK
Tính thể tích vật thể T nằm giữa hai mặt phẳng x = 0 và x = π, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ π) là một hình vuông cạnh là 2√(sinx).
Lời giải:
Diện tích thiết diện là
![]()
Vật thể tích của vật T cần tìm là:
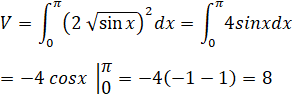
Bài 37 Trang 175 SGK
Cho hình phẳng A giới hạn bởi các đường y = x2, y = 0, x = 0 và x = 2. Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.
Lời giải:
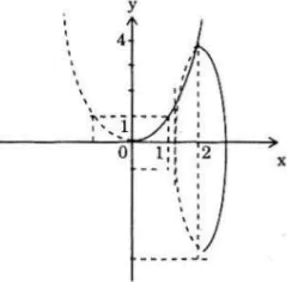
Thể tích khối tròn xoay tạo thành được tính theo công thức
![]()
Vậy thể tích cần tìm là: ![]()
Bài 38 Trang 175 SGK
Cho hình phẳng A giới hạn bởi các đường cong y = cosx, y = 0, x = 0, x = π/4. Tính thể tích khối tròn xoay tạo thành khi quay quanh hình A quanh trục hoành.
Lời giải:
Thể tích cần tìm là:
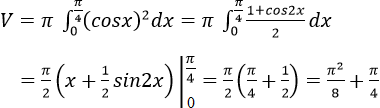
Bài 39 Trang 175 SGK
Cho hình phẳng A giới hạn bởi các đường y = x.ex/2, y = 0, x = 0, x = 1. Tính thể tích khối tròn xoay tạo thành khi quay hình A quanh trục hoành.
Lời giải:
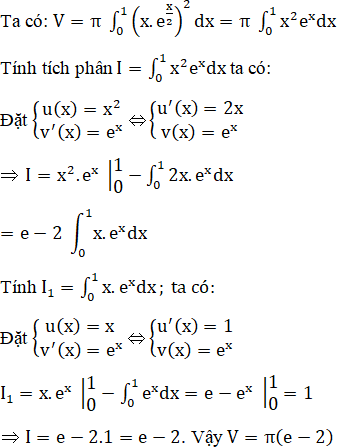
Bài 40 Trang 175 SGK
Cho hình phẳng B giới hạn bởi các đường ![]()
Tính thể tích của khối tròn xoay tạo thành khí quay hình B quanh trục tung.
Lời giải:
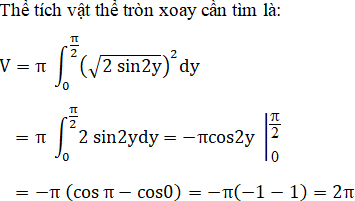

















Bình Luận
Để Lại Bình Luận Của Bạn