Câu hỏi và bài tập Ôn tập cuối năm | Bài giải GIẢI TÍCH 12 (Nâng Cao) | CHƯƠNG IV - SỐ PHỨC - Lớp 12 - Sách Bài Giải

I - BÀI TẬP TỰ LUẬN

Câu 1 trang 211 SGK

Chứng minh rằng hàm số f(x) = e^x – x – 1 đồng biến trên nửa khoảng [0; +∞)

b) Từ đó suy ra e^x > x + 1 với mọi x > 0.

Lời giải:

a) Ta có: f’(x) = (e^x – x – 1 )' = e^x – 1

f' (x) ≥ 0 ⇔ e^x – 1 ≥ 0 ⇔ e^x ≥ 1 ⇔ x ≥ 0

Vậy f(x) đồng biến trên [0; +∞)

b) Vì f(x) =  e^x – x – 1 đồng biến trên [0; +∞) nên:

f(x) > f(0) với mọi x > 0, mà f(0) = 0 nên ta có:

f(x) > 0 ⇔ e^x – x – 1 > 0 ⇔  e^x > x + 1 (đpcm)

Câu 2 trang 211 SGK

a) Khảo sát và vẽ đồ thị hàm số f(x) = 2x³ – 3x² – 12x – 10

b) Chứng minh rằng phương trình 2x³ – 3x² – 12x – 10 = 0 có nghiệm thực duy nhất.

c) Gọi nghiệm thực duy nhất của hàm số là α. Chứng minh rằng 3,5 < α < 3,6.

Lời giải:

a) Tập xác định: R

f' (z) = 6x² – 6x – 12; f(x) = 0 ⇔ x = -1 ; x = 2.

f'' (x) = 12x – 6; f''(x) = 0 ⇔ x = 1/2.

Bảng biến thiên

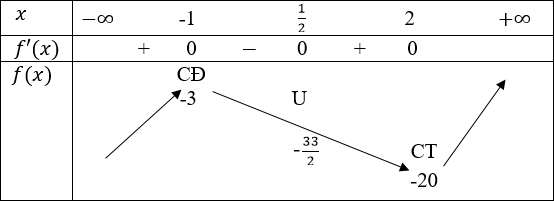
Đồ thị

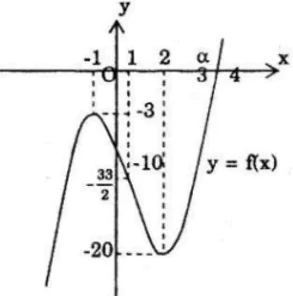
b) Nhìn vào đồ thị của hàm số y = 2x³ – 3x² – 12x – 10 = 0 ta thấy đồ thị chỉ cắt Ox tại 1 điểm duy nhất, nên phương trình:

2x³ – 3x² – 12x – 10 có 1 nghiệm duy nhất.

c) Xét f(x) = 2x³ – 3x² – 12x – 10. Ta có f(3, 5). f(3, 6) < 0 mà f(x) là hàm liên tục nên f(x) có một nghiệm α ∈ (3,5; 3,6) (đpcm)

Câu 3 trang 211 SGK

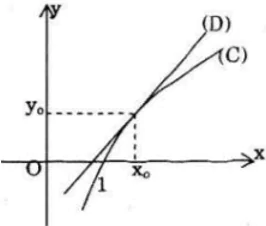
Gọi (C) là đồ thị hàm số của y = lnx và (D) là một tiếp tuyến bất kì của (C). Chứng minh rằng trên khoảng (0; +∞), C nằm ở phía dưới của đường thẳng (D).

Lời giải:

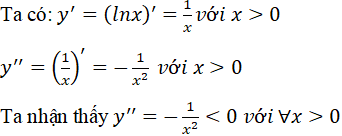
nên đồ thị hàm số y = lnx lồi trên (0; +∞) nên đường tiếp tuyến D luôn nằm trên đồ thị C. (đpcm)

Câu 4 trang 212 SGK

Một xưởng in có 8 máy in, mỗi máy in được 3600 bản trong một giờ. Chi phí để vận hành một trong mỗi lần là 50 nghìn đồng. Chi phí cho n máy chạy trong một giờ là 10(6n + 10) nghìn đồng. Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy để được lãi nhiều nhất?

Lời giải:

Giả sử dụng máy n máy để in (n = 1; 2; 3; 4; 5; 6; 7; 8).

Khi đó, tổng chi phí để in 50000 tờ quảng cáo là:

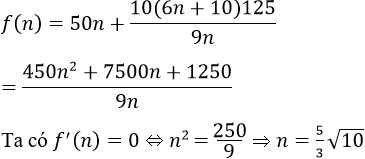
Bảng biến thiên của f(n)

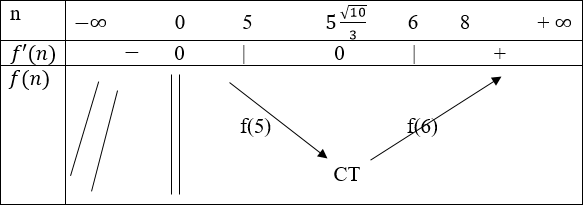
Để ta được lãi nhiều nhất thì tổng chi phí phải là ít nhất.

Vậy ta cần tìm n ∈{1; 2; 3; 4; 5; 6; 7; 8} để f(n) nhỏ nhất. ta có f(5) < f(6), kết hợp với bảng biến thiên của f(n) thì khi n = 5 tổng chi phí sẽ bé nhất.

Vậy nên chọn 5 máy.

Câu 5 trang 212 SGK

Tìm giá trị lớn nhất và nhỏ nhất của hàm số

trên đoạn [0; 1]

Lời giải:

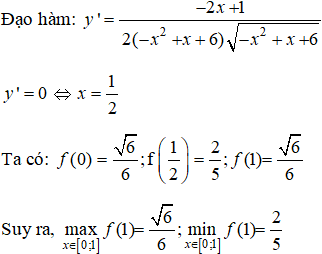
Câu 6 trang 212 SGK

a) Cho P(x) = 4^x/(4x+2) và hai số a, b thỏa mãn a + b = 1. Hãy tính P(a) + P(b).

b) Hãy so sánh A = ³√18 và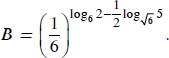

Lời giải:

a) Ta có:

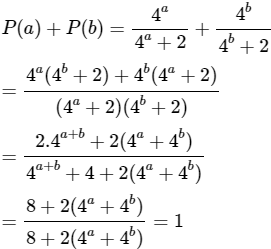
b) Ta có:

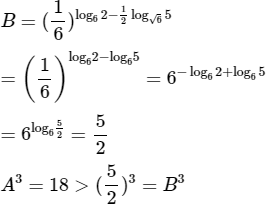
Suy ra A > B.

Câu 7 trang 212 SGK

a) Chứng minh rằng nếu a và b là hai số dương thỏa mãn a² + b² = 7ab thì

b) Biết a và b là hai số dương, a ≠ 1 sao cho log_ab = √3. Hãy tính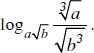

Lời giải:

a) Ta có:

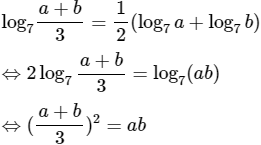
⇔ (a + b³)² = ab

⇔ a² + 2ab + b² = 9ab

⇔ a² + b² = 7ab (đpcm)

b) Ta có:

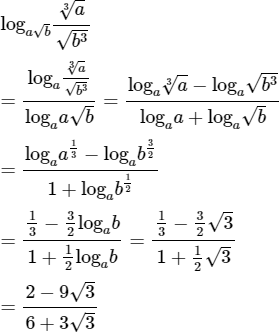
Câu 8 trang 212 SGK

a) Tính đạo hàm của các hàm số: y = cosx.e^2tanx và y = log₂(sin⁡x).

b) Chứng minh rằng hàm số y = e^4x + 2e^-x thõa mãn hệ thức y''' – 13y' – 12y = 0

Lời giải:

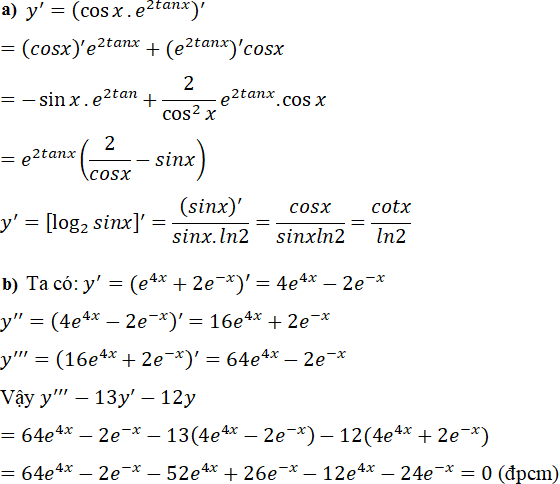
Câu 9 trang 212 SGK

a) Vẽ đồ thị của hàm số y = 2^x, y = (√2)^x và y = (√3)^x trên cùng một mặt phẳng tọa độ. Hãy nêu nhận xét về vị trị tương đối của ba đồ thị đó.

b) Vẽ đồ thị hàm số y = log₃x. Từ đó suy ra đồ thị của hàm số y = 2 + log₃⁡x và đồ thị của hàm số y = log₃(x + 2).

Lời giải:

a) Vẽ đồ thị các hàm số: y = 2^x, y = (√2)^x và y = (√3)^x

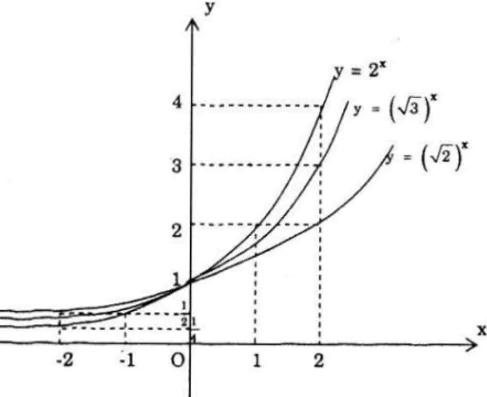
Nhận xét:

Trong khoảng (-∞; 0) đồ thị sắp xếp theo thứ tự từ trên xuống dưới là: y = (√2)^x , y = (√3)^x, y = 2^x

Đồ thị cả ba hàm số đi qua điểm (0; 1)

Trong khoảng (0; +∞) đồ thị sắp xếp theo thứ tự từ trên xuống dưới là: y = 2^x, y = (√3)^x, y = (√2)^x

Như vậy “độ dốc” của đồ thị hàm số tăng theo giá trị cơ số: √2 < √3 < 2.

b) Vẽ đồ thị hàm số y = log₃x (C)

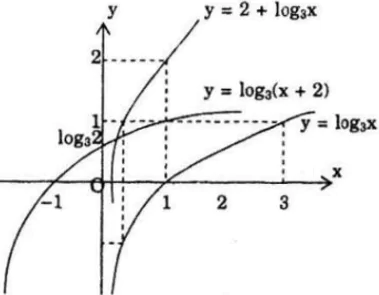
Đồ thị hàm số y = 2 + log₃x có được bằng cách tịnh tiến (C) lên trên theo phương Oy 2 đơn vị.

Đồ thị hàm số y = log₃(x + 2) có được bằng cách tính tiến (C) sang bên trái theo phương Ox 2 đơn vị.

Câu 10 trang 212 SGK

Giải các phương trình và hệ phương trình sau

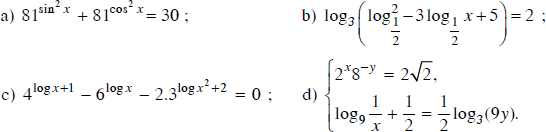
Lời giải:

a)

b) Điều kiện: x > 0.

Ta có:

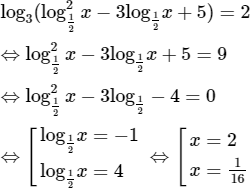
Vậy S = {1/16; 2}.

c) Điều kiện: x > 0. 

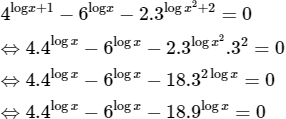
Chia hai vế phương trình 4^logx ta được:

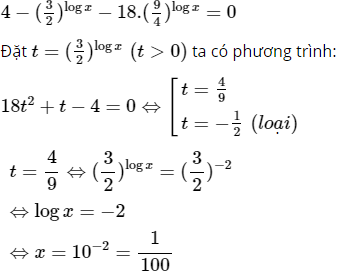
d) Điều kiện: x > 0; y > 0.

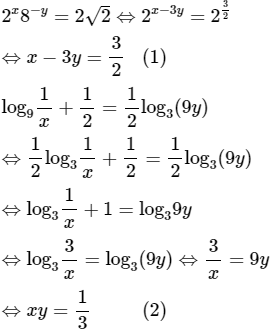
Từ (1) và (2) ta có hệ phương trình:

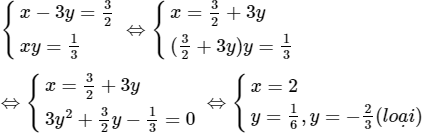
Vậy S = {(2, 1/6)}.

Câu 11 trang 213 SGK

Tìm tập xác định của các hàm số sau

a) y = log[1 – log(x² − 5x + 16)]

Lời giải:

a) Hàm số xác định khi và khi chỉ khi:

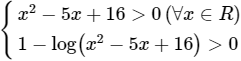
⇔ log(x² − 5x + 16) < 1 

⇔ x² − 5x + 16 < 10 

⇔ x² − 5x + 6< 0 

⇔ 2 < x <3

Vậy D = (2, 3).

b) Hàm số xác định khi và khi chỉ khi:

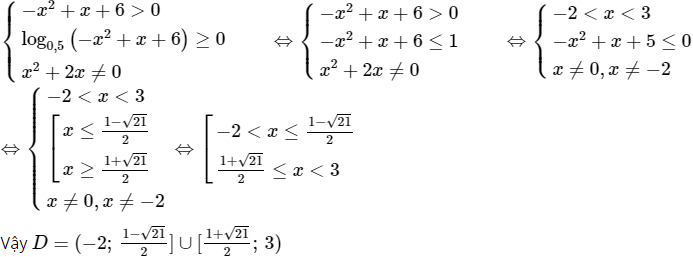
Câu 12 trang 213 SGK

Tìm nguyên hàm của mỗi hàm số sau

a) y = x³ (1 + x⁴)³ ;

b) y = cosx sin2x ;

b) y = x/cos²x .

Lời giải:

a) Đặt u = 1 + x⁴

⇒ du = 4x³dx

⇒ x³dx = du/4

∫x³(1 + x⁴)dx

=14∫u³du

= u⁴/16 + C

= 1/16(1 + x⁴)⁴ + C

b) Ta có:

∫sin2x.cosxdx = 1/2∫(sin3x + sinx)dx 

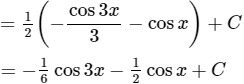
Cách khác:

Tìm F(x) = ∫cosx.sin2x dx=2 ∫cos2x.sinxdx

Đặt cosx = u ⇒ -sinxdx = du ⇒ sinxdx = -du.

Ta có:

F(x) = 2∫u².(−du) = −2∫u²du = −2/3u³ + C = −2/3cos³u + C

c) Đặt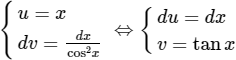

Do đó:

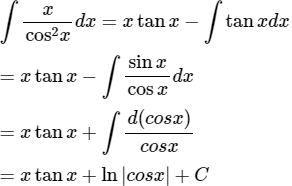
Câu 13 trang 213 SGK

Tìm hàm số f, biết rằng f′(x) = 8sin2(x + π/12) và f(0) = 8.

Lời giải:

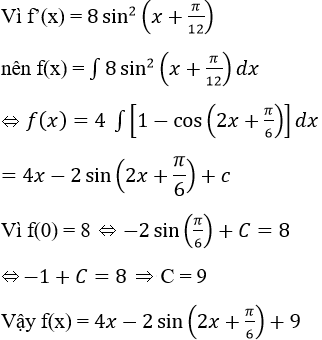
Câu 14 trang 213 SGK

Tính các tính phân sau:

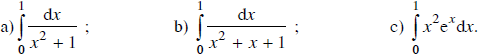
Lời giải:

a) Đặt x = tant ⇒ dx = 1/cos²t dt = (1 + tan²t) dt

Đổi cận:

x = 0 ⇒ t = 0

x = 1 ⇒ t = π/4

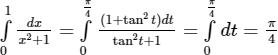
b) Ta có:

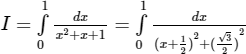
Đặt x + 1/2 = √3/2tant 

⇒ dx = √3/2(1 + tan²t)dt

Đổi cận:

x = 0 ⇒ t = π/6

x = 1 ⇒ t = π/3

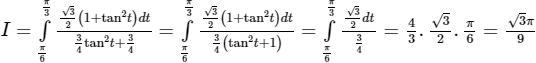
c) Đặt

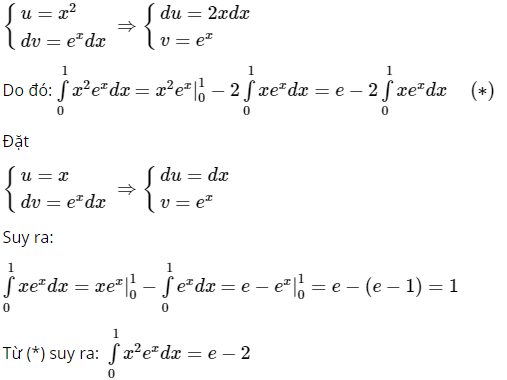
Câu 15 trang 213 SGK

Tính diện tích các hình phẳng giới hạn bởi các đường

a) y + x² = 0 và y + 3x² = 2;

b) y² – 4x = 4 và 4x – y = 16.

Lời giải:

a) Phương trình hoành độ giao điểm của hai đường cong là:

-x² = 2 – 3x² ⇔ x²  = 1 ⇔ x = ± 1

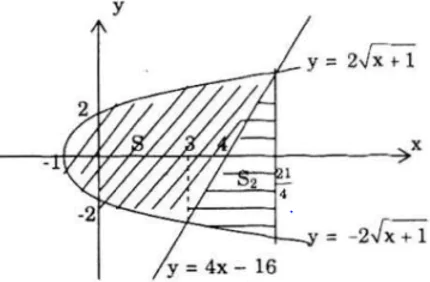
Với −1 ≤ x ≤ 1 thì 2x² − 2 ≤ 0 ⇒ ∣2x² − 2∣ = 2 − 2x²

Diện tích cần tìm là:

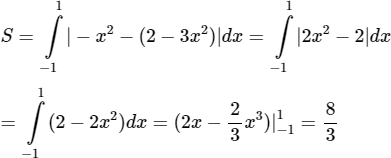
b) Ta có:

y² − 4x = 4 ⇔ x = (y² − 4)/4

4x − y = 16 ⇔ x = (y + 16)/4

Phương trình tung độ giao điểm của hai đường cong là:

y² − 4 = y + 16 ⇔ y² − y − 20 = 0 ⇔ y = −4 hoặc y = 5

Với y ∈ (−4; 5) ⇒ y² − y − 20 ≤ 0 ⇒ ∣y² − y − 20∣ = −y² + y + 20

Diện tích cần tìm là:

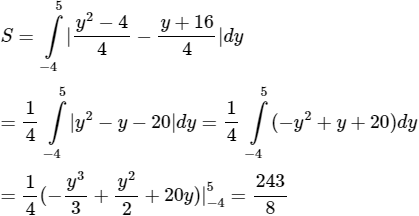
Câu 16 trang 213 SGK

a) Cho hình thang cong A giới hạn bởi đồ thị hàm số y = ex, trục hoành và các đường thẳng x = 0 và x = 1.

Tính thể tích của khối tròn xoay tạo được khi quay A quanh trục hoành.

b) Cho hình phẳng B giới hạn bởi parabol y = x² + 1 và đường thẳng y = 2.

Tính thể tích khối tròn xoay tạo được khi quay B quanh trục tung.

Lời giải:

a) Thể tích cần tìm là:

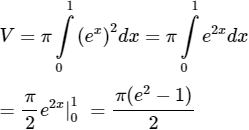
b) Ta có: 

y = x² + 1 ⇔ x² = y − 1 ⇔ x = ±√(y − 1)

x = 0 thì y = 1.

Thể tích cần tìm là:

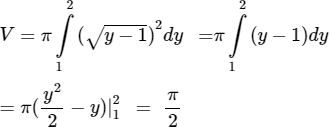
Câu 17 trang 213 SGK

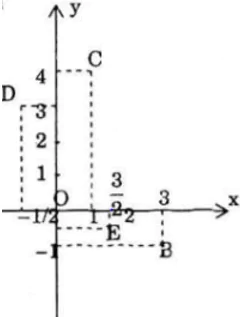
Cho các số phức z₁= 1 + i; z₂ = 1 – 2i. Hãy tính và biểu diễn hình học các số phức:

Lời giải:

Ta có: z₁² = (1 + i)² = 1 + 2i + i² = 1 + 2i – 1 = 2i

z₁ z₂ = (1 + i)(1 – 2i) = 1 + i – 2i – 2i² = 1 – i + 2 = 3 – i

2z₁ – z₂ = 2(1 + i) – (1 – 2i) = 1 + 4i 

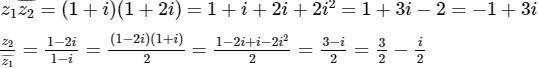
Câu 18 trang 214 SGK

Tính

a) (√3 + i)² – (√3 – i)²;

b) (√3 + i)² + (√3 – i)²;

c) (√3 + i)³ – (√3 – i)³;

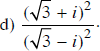
Lời giải:

a) (√3 + i)² – (√3 – i)²= (3 + 2√3 i –1) – (3 – 2√3 i – 1) = 4√3 i

b) (√3 + i)²+ (√3 – i)² = (3 + 2√3 i – 1) + (3 – 2√3 i – 1) = 4

c) (√3 + i)³ – (√3 – i)³ = (3√3 + 9i – 3√3 – i) – (3√3 – 9i –3 √3 + i) = 16i

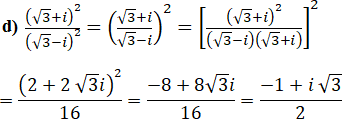
Câu 19 trang 214 SGK

a) Xác định phần thực của số phức biết rằng |z| = 1 và z ≠ 1.

b) Chứng minh rằng nếu là số ảo thì |z| = 1.

Lời giải:

a) Giả sử z = a + bi với a² + b² = 1 và a + bi ≠ 1

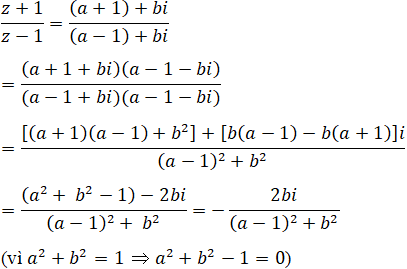
Vậy số phức (z + 1)/(z – 1) có phần thực bằng 0.

Cách khác:

Ta có:

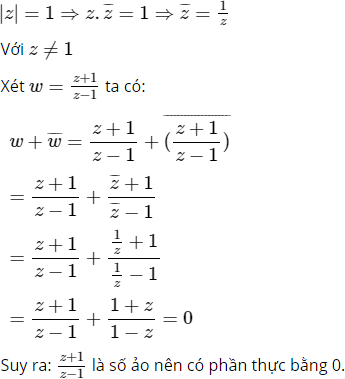
b) Theo câu a, ta có:

Nên (z + 1)/(z – 1) là số ảo thì a² + b² – 1 = 0 ⇔ a² + b² = 1 ⇔ |z| = 1 (đpcm)

Cách khác:

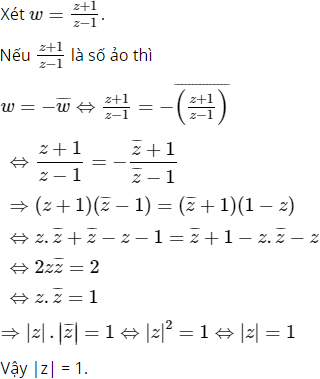
Câu 20 trang 214 SGK

Xác định tập hợp các điểm M trên mặt phẳng phức biểu diễn các số phức (1 + i√3)z + 2, trong đó |z – 1| ≤ 2

Lời giải:

Giả sử z = x + yi, vì |z – 1| ≤ 2 nên (x – 1)² + y² ≤ 4 (1)

Ta có:

w = (1 + √3 i)z + 2 = (1 + √3 i)(x + yi) + 2 = (x –  √3 y + 2) +i(x√3 + y)

Gọi N là điểm biểu diễn số phức w ⇒ N(x – √3 y + 2; x√3 + y)

Từ (1) ta có: 4[(x – 1)² + y²] ≤ 16 ⇔ (x – 1)²+3y²] + [3(x – 1)²+ y²] ≤ 16

⇔ (x –  1 – √3 y)² + (√3 (x – 1) + y)² ≤ 16 ⇔ (xN – 1)² + (yN – √3)² ≤ 16

Vậy tập hợp các điểm N nằm trong hình tròn có tâm A(1; √3) có bán kính R = 4.

Bài 21 trang 214 SGK

Tìm căn bậc hai của mỗi số phức:

-8 + 6i;  3 + 4i;  1 – 2√2 i

Lời giải:

Gọi a+bi là căn bậc hai của -8 + 6i, ta có:

(a + bi)² = -8 + 6i ⇔ (a² – b²) + 2abi = -8 + 6i

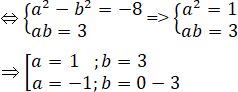
Vậy số -8 + 6i căn bậc hai là: 1 + 3i; -1 – 3i.

Tương tự, số 3 + 4i có căn bậc hai là: 2 + i; - 2 – i;

Số 1 – 2√2 i có căn bậc hai là: √2 – i và -√2+i

Bài 22 trang 214 SGK

Giải phương trình sau trên C:

a) : z² – 3z + 3 + i = 0.

b) z² – (cos⁡φ + i sin⁡φ)z + i sin⁡φcos⁡φ = 0.

Lời giải:

a) Ta có biệt số ∆ = (-3)² – 4.(3 + i)= -3 – 4i = (2i – 1)² nên phương trình có hai nghiệm là z₁ = i + 1; z₂ = 2 – i

b) Ta có biệt hiệu số

∆ = (cos⁡φ + i sin⁡φ )² – 4i sin⁡φ. cos⁡φ

= cos²φ + 2i.cosφ.sinφ – sin²φ – 4isinφ.cosφ = cos⁡(-2φ) + i sin⁡(-2φ)

∆ có hai căn bậc hai là: cos⁡(-φ) + i sin⁡(-φ) và (-cos⁡(-φ) – i sin⁡(-φ)

Nên phương trình có nghiệm là:

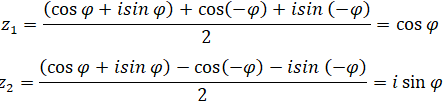
Bài 23 trang 214 SGK

Tính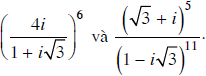

Lời giải:

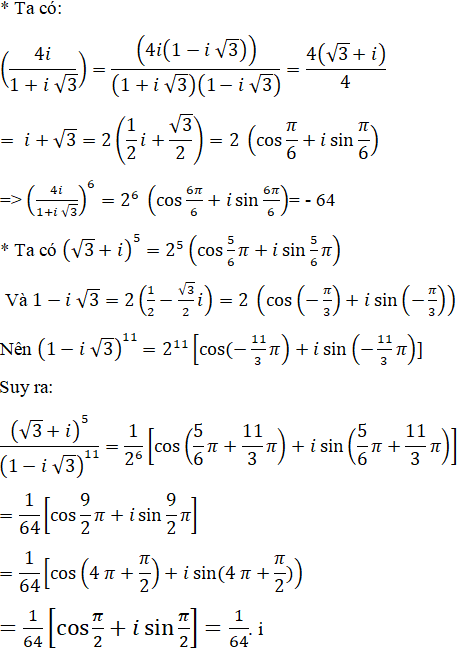
II - BÀI TẬP TRẮC NGHIỆM KHÁCH QUAN

Trong mỗi bài tập dưới đây, hãy chọn một phương án trong các phương án đã cho để được khẳng định đúng.

Bài 24 trang 214 SGK

Hàm số

(A) Đồng biến trên mỗi khoảng (−∞; 1) và (3; +∞);

(B) Nghịch biến trên mỗi khoảng (−∞; 1) và (3; +∞);

(C) Đồng biến trên khoảng (−∞; 1) và nghịch biến trên khoảng (3; +∞);

(D) Nghịch biến trên khoảng (−∞; 1) và đồng biến trên khoảng(3; +∞).

Lời giải:

Ta có: 

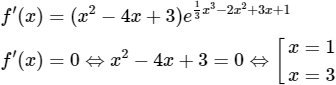
Ta có bảng biến thiên:

Chọn (A).

Bài 25 trang 215 SGK

Hàm số f(x) = sin²x – 2sinx có giá trị nhỏ nhất là

(A) −1/2;

(B) 0;

(C) -1;

(D) −1/3.

Lời giải:

Đặt  t = sin x; t ∈ [-1, 1]

f(x) = g(t) = t2 – 2t

g’ = 2t – 2 = 0 ⇔ t = 1

g(-1) = 3

g(1) = -1

Vậy min_x∈R f(x) = -1

Chọn (C).

Bài 26 trang 215 SGK

Gọi (C) là đồ thị của hàm số y = √(x²+x). Khi đó

(A) Đường thẳng y = x + 1 là tiệm cận xiên của (C) (khi x → +∞);

(B) Đường thẳng y = x + 1/2 là tiệm cận xiên của (C) (khi x → +∞);

(C) Đường thẳng y = -x là tiệm cận xiên của (C) (khi x → +∞);

(D) Đồ thị (C) không có tiệm cận xiên (khi x → +∞).

Lời giải:

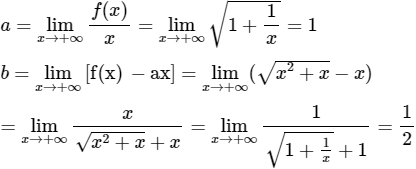
Vậy y = x +1/2 là tiệm cận xiên của (C) khi x → +∞.

Chọn (B).

Bài 27 trang 215 SGK

Đồ thị của hàm số y = x³ – x + 1 tiếp xúc với điểm (1, 1) với

(A) Parabol y = 2x² – 1;

(B) Parabol y = x²;

(C) Parabol y = -x² + 2x;

(D) Đường thẳng y = 2x + 1.

Lời giải:

Xét f(x) = x3 – x + 1 ; g(x) = x²

Ta có:

Nên đồ thị hàm số y = x³ – x + 1 tiếp xúc với (P)

y = x² tại (1, 1)

Chọn (B).

Bài 28 trang 215 SGK

Cho hai số dương a và b. Đặt

Khi đó:

(A) X > Y;

(B) X < Y;

(C) X ≥ Y;

(D) X ≤ Y.

Lời giải:

Ta có: 

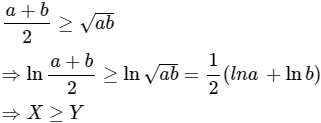
Chọn (C).

Bài 29 trang 215 SGK

Cho hai số không âm a và b. Đặt

Khi đó:

(A) X > Y;

(B) X < Y;

(C) X ≥ Y;

(D) X ≤ Y.

Lời giải:

Ta có:

 

Vậy chọn (D).

Bài 30 trang 215 SGK

Cho (C) là đồ thị của hàm số y = log₂x. Ta có thể suy ra đồ thị của hàm số y = log₂2(x + 3) bằng cách tịnh tiến (C) theo vectơ:

Lời giải:

Ta có:

log₂2(x + 3) = 1 + log2 (x + 3)

y = log₂x → Tịnh tiến trái 3 đơn vị

y = log₂ (x + 3) → Tịnh tiến lên trên 1 đơn vị → y = 1 + log₂ (x + 3)

Chọn (C).

Bài 31 trang 216 SGK

Cho hàm số f(x) = log5(x² + 1). Khi đó:

(A) f′(1) = 1/2ln5;

(B) f′(1) = 1/ln5;

(C) f′(1) = 3/2ln5;

(D) f′(1) = 2/ln5.

Lời giải:

Ta có:

Chọn (B).

Bài 32 trang 216 SGK

Biết rằng đồ thị của hàm số y = a^x và đồ thị của hàm số y = log_bx cắt nhau tại điểm (√2⁻¹; √2). Khi đó

(A) a > 1 và b > 1.

(B) a > 1 và 0 < b < 1.

(C) 0 < a < 1 và b > 1.

(D) 0 < a < 1 và 0 < b < 1.

Lời giải:

Ta có:

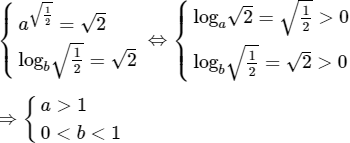
Chọn (B).

Bài 33 trang 216 SGK

Cho hàm số

Khi đó

(A) ∫f(x)dx = 2x³/3 − 3/x + C;

(B) ∫f(x)dx = 2x³/3 + 3/x + C;

(C) ∫f(x)dx = 2x³ − 3/x + C;

(D) ∫f(x)dx = 2x³/3 + 3/2x + C.

Lời giải:

∫f(x)dx = ∫(2x² + 3/x²)dx = 2x³/3 − 3/x + C

Chọn (A).

Bài 34 trang 216 SGK

Nếu a là một số thỏa mãn các điều kiện:

thì

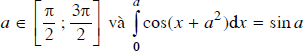
(A) a = π;

(B) a = √π;

(C) a = 2√π;

(D) a = √(2π).

Lời giải:

Ta có:

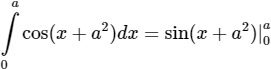
= sin(a + a²) − sina² = sina

⇔ sin(a + a²) = sina² + sina

Với a = √2π ⇒ sin(√(2π) + 2π) = sin2π + sin√(2π)

⇔sin√(2π) = sin√(2π)

Chọn (D).

Bài 35 trang 216 SGK

Gọi S là tập hợp các số nguyên dương k thỏa mãn điều kiện

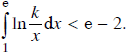
Khi đó:

(A) S = {1};

(B) S = {2};

(C) S = {1, 2};

(D) S = Ø.

Lời giải:

Ta có:

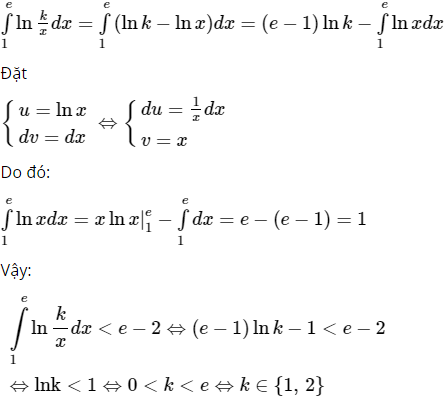
Chọn (C).

Bài 36 trang 217 SGK

Cho số phức z tùy ý. Xét các số phức

Khi đó:

(A) α là số thực, β là số thực.

(B) α là số thực, β là số ảo.

(C) α là số ảo, β là số thực.

(D) α là số ảo, β là số ảo.

Lời giải:

Giả sử z = a + bi, ta có:

α = (a + bi)² + (a − bi)² = 2a² − 2b²

Vậy α ∈ R

β = (a + bi)(a − bi) + i(a + bi − a + bi)

= a² + b² − 2b ∈ R

Vậy chọn (A).

Bài 37 trang 217 SGK

Cho số phức tùy ý z. Xét các số phức

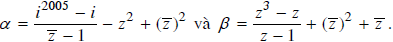
Khi đó:

(A) α là số thực, β là số thực;

(B) α là số thực, β là số ảo;

(C) α là số ảo, β là số thực;

(D) α là số ảo, β là số ảo.

Lời giải:

Ta có:

i²⁰⁰⁵ = i

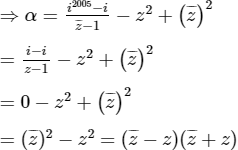
= (a − bi − a − bi)(a − bi + a + bi) 

= −2bi.2a = −4abi là số ảo.

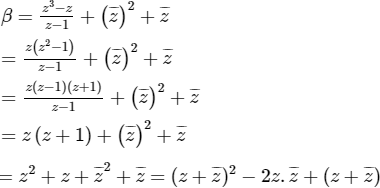
= (a + bi + a − bi)² − 2(a² + b²) + (a + bi + a − bi) 

= 4a² − 2(a² + b²) + 2a

= 2a² − 2b² + 2a là số thực.

Chọn (C).

Bài 38 trang 217 SGK

Nếu môđun của số phức z bằng r (r > 0) thì môdun của số phức (1 – i)²z bằng:

(A) 4r;

(B) 2r;

(C) r√2;

(D) r.

Lời giải:

(1 − i)² = 1 − 2i + i² = −2i

⇒∣(1 − i)² = |−2i| = 2

⇒∣(1 − i)²z∣ = ∣(1 − i)²∣.|z|

= 2r

Chọn (B).