Bài 7. Phương trình mũ và lôgarit | Bài giải GIẢI TÍCH 12 (Nâng Cao) | CHƯƠNG II - HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT - Lớp 12 - Sách Bài Giải

Bài 63 trang 123 SGK

Giải các phương trình sau:

a) (2 + √3)^2x = 2 – √3;

c) 2.3^{x + 1} – 6.3^{x – 1} – 3^x = 9;

d) log₃(3^x + 8) = 2 + x.

Lời giải:

a) (2 + √3)^2x = 2 – √3

⇔ (2 + √3)^2x = (2 + √3)^-1

⇔ 2x = -1

⇔ x = -1/2

Vậy tập nghiệm của phương trình S = {-1/2}.

Cách khác:

(2 + √3)^2x = 2 – √3

⇔ (2 – √3)^-2x = 2 – √3

⇔ -2x = 1

⇔ x = -1/2

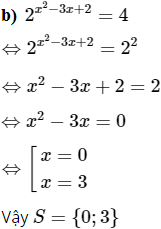
c) 2.3^{x + 1} – 6.3^{x – 1} – 3^x = 9

⇔ 2.3^x.3  – 6.3^x.(1/3) – 3^x = 9

⇔ 6.3^x – 2.3^x – 3^x = 9

⇔ 3.3^x = 9

⇔ 3^x = 3

⇔ x = 1

Vậy S = {1}.

d) log₃⁡(3^x + 8) = 2 + x

⇔ 3^x + 8 = 3^{2 + x}

⇔ 3^x + 8 = 9.3^x

⇔ 8.3^x = 8

⇔ 3^x = 1

⇔ x = 0

Vậy S = {0}.

Bài 64 trang 124 SGK

Giải các phương trình sau:

a) log₂[x(x – 1)] = 1                                                                     b) log_2⁡x + log₂(x – 1 ) = 1

Lời giải:

a) Điều kiện: x.(x – 1) > 0 hay

Khi đó, log₂[x(x – 1)] = 1

⇔ x.(x – 1) = 2

⇔ x² – x – 2 = 0

⇔ x = -1 hoặc x = 2

Vậy nghiệm của phương trình đã cho là: x = -1; x = 2.

b) Điều kiện: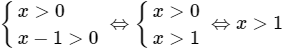

Khi đó, log₂⁡x + log₂⁡(x – 1) = 1

⇔ log₂[x(x – 1)] = 1

⇔ x.(x – 1) = 2

⇔ x² – x – 2 = 0

⇔ x = -1 (loại) hoặc x = 2

Vậy phương trình có một nghiệm là x = 2.

Bài 65 trang 124 SGK

Trên mặt mỗi chiếc radio đều có các vạch chia để người sử dụng dễ dàng chọn đúng song radio cần tìm. Biết vạch chia ở vị trị cách vạch tâm cũng bên trái một khoảng d(cm) thì ứng với tần số F = k.a^d (kHz), trong đó k và a là hai hằng số được chọn sao cho vạch tận cùng bên trái ứng với tần số 53kHz, vạch tậm cùng bên phải ứng với tần số 160kHz và hai vạch nàu cách nhau 12cm.

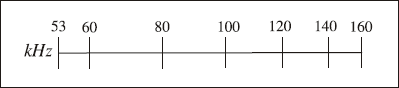
a) Tính k và a (tính a chính xác đến hàng phần nghìn)

b) Giả sử cho F, hãy giải thích Phương trình k.a^d = F với ẩn d.

c) Áp dụng kết quả của b, hãy điền vào ô trống trong bảng sau (kết quả chính xác đến phần trăm).

F	53	60	80	100	120	140	160
d

Lời giải:

a) Theo giả thiết ta có: d = 0 ⇒ F = 53 ⇔ k.a⁰ = 53 ⇔ k = 53

Và d = 12 ⇒ F = 160 ⇔ k.a¹²=160

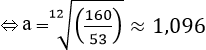
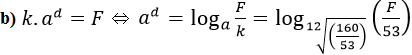
c) Từ câu b) ⇒ d = 25,119.lgF – 43,312

(do yêu cầu kết quả tính chính xác đến hàng phần trăm)

Vậy ta có bảng:

F	53	60	80	100	120	140	160
d	0	1,35	4,49	6,93	8,91	10,60	12

Bài 66 trang 124 SGK

Giải các phương trình sau:

a) 2^{x + 1}.5^x = 200                                                                     b) 0,125.4^{2x – 3} = (4√2)^x

Lời giải:

a) 2^{x + 1}.5^x = 200

⇔ 2.10^x = 200

⇔ 10x = 100

⇔ x = 2

Cách khác:

2^{x + 1}.5^x = 200

⇔ 2^{x + 1}.5^x = 2³.5²

⇔ 2^{x – 2}.5^{x – 2} = 1

⇔ 10^{x – 2} = 1

⇔ x – 2 = 0

⇔ x = 2

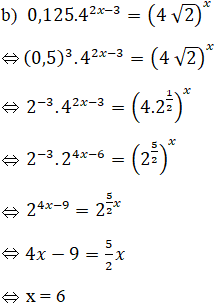
Bài 67 trang 124 SGK

Giải các phương trình sau:

a) log₂⁡x + log₄⁡x = log_1/2⁡√3                                                                     b) log_√3⁡x.log₃x.log₉⁡x = 8

Lời giải:

a) log₂⁡x + log₄⁡x = log_1/2⁡√3

b) log_√3⁡x.log₃x.log₉⁡x = 8  Điều kiện: x > 0

⇔ log_3⁡^(1/2)x.log₃⁡x.log_3²x = 8

⇔ 2log₃⁡x.log₃⁡x.(1/2)log₃x = 8

⇔ (log₃⁡x)³ = 8

⇔ log_3⁡x = 2

⇔ x = 3² = 9

Kết hợp với điều kiện, vậy nghiệm của phương trình đã cho là x = 9.

Bài 68 trang 124 SGK

Giải các phương trình sau:

a) 3^x+1 + 18.3 ^-x = 29                                                                     

b) 27^x + 12^x = 2.8^x (Hướng dẫn: Chia cả hai vế cho 2^3x rồi đặt t = (3/2)^x).

Lời giải:

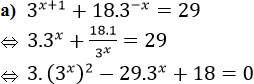
Đặt t = 3^x (t > 0).

Phương trình trở thành:

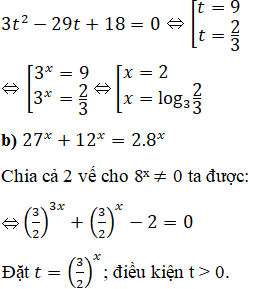
Phương trình trở thành: t³ + t – 2 = 0

⇔ (t – 1)(t² + t + 2) = 0 ⇔ t = 1

Với t = 1 ⇒ (3/2)^x = 1 ⇔ x = 0.

Bài 69 trang 124 SGK

Giải các phương trình sau:

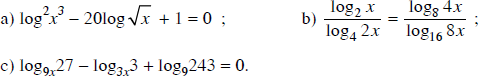
Lời giải:

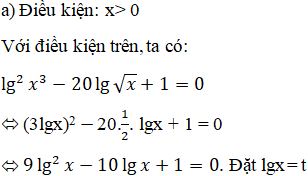
Phương trình trở thành:

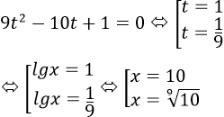
Vậy phương trình có hai nghiệm: x = 10; x = ⁹√10.

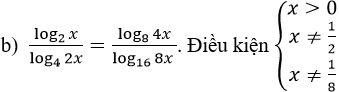
Phương trình tương dương với:

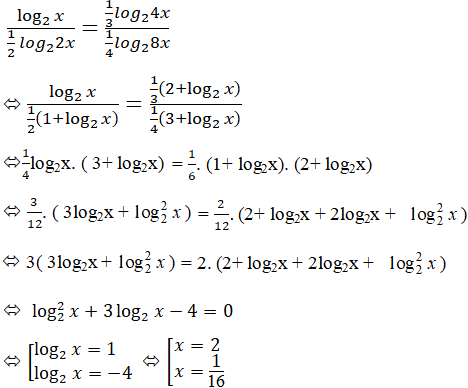
Kết hợp với điều kiện, vậy phương trình đã cho có tập nghiệm là: S = {1; 1/16}.

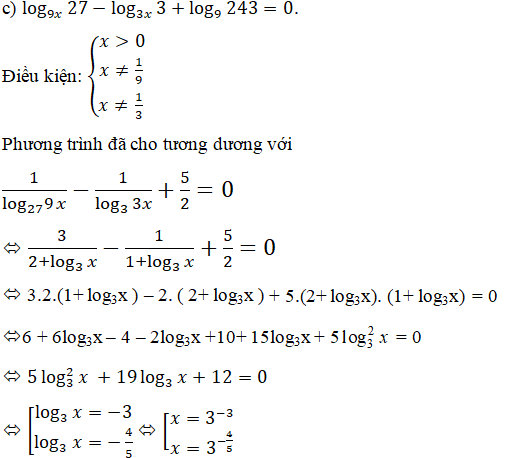
Kết hợp với điều kiện, vậy phương trình có tập nghiệm là: S = {3^-3; 3^(-4/5)}.

Bài 70 trang 125 SGK

Giải các phương trình sau:

a) 3^4x = 4^3x;

b) 3^{2 – log₃⁡x} = 81x;

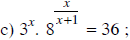
d) x⁶.5^-log_x5 = 5^-5.

Lời giải:

a) 3^4x = 4^3x

Lấy logarit cơ số 3 hai vế, ta được:

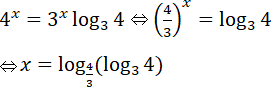
Vậy S = {log_4/3(log₃4)}.

b) 3^{2 – log₃⁡x} = 81x. Điều kiện x > 0.

Lấy logarit cơ số 3 hai vế, ta được:

2 – log₃⁡x = 4 + log₃⁡x

⇔ log₃⁡x = -1

⇔ x = 3^-1 = 1/3

Vậy S = {1/3}.

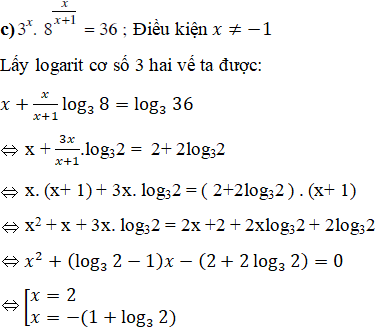
Vậy S = {2;  –1 – log₃2}.

d) x⁶.5^-log_x5 = 5^-5. Điều kiện 0 < x ≠ 1.

Logarit hóa 2 vế theo cơ số x, ta được:

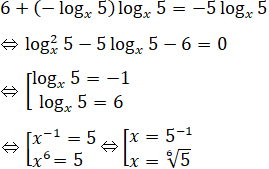
Vậy S = {5^-1; ⁶√5}.

Bài 71 trang 125 SGK

Giải các phương trình sau:

a) 2^x = 3 – x;                                                                                b) log₂x = 3 – x.

Lời giải:

a) Ta thấy x = 1 là nghiệm. Ta chứng minh x = 1 là nghiệm duy nhất. Thật vậy:

+ Nếu x < 1: 2^x < 2¹ < 2

Phương trình vô nghiệm với x < 1.

+ Nếu x > 1: 2^x > 2¹ = 2

Phương trình vô nghiệm với x > 2. Vậy Phương trình có nghiệm x = 1.

b) log₂⁡x = 3 – x. điều kiện: x > 0.

Dễ thấy x = 2 là nghiệm của Phương trình, ta chứng minh x = 2 là nghiệm duy nhất. thật vậy:

+ Nếu x > 2: log₂⁡x > log_2⁡2 = 1

Phương trình vô nghiệm x > 2.

+ Nếu 0 < x < 2: log₂⁡x < log₂⁡2 = 1

Phương trình vô nghiệm 0 < x < 2.

Vậy phương trình có nghiệm duy nhất x = 2.