Nội Dung Chính
Bài 26 trang 167 SGK
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = sinx + 1, trục hoành và hai đường thẳng x = 0 và x = 7π/6.
Lời giải:
Ta thấy sinx + 1 ≥ 0 ∀x ∈ (0; 7π/6) nên diện tích S cần tìm bằng:
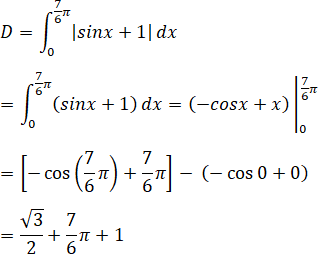
Bài 27 Trang 167 SGK
Tính diện tích hình phẳng bởi giới hạn bởi:
a) Đồ thị hàm số y = cos2x, trục hoành, trục tung và đường thẳng x = π;
b) Đồ thị hai hàm số y = √x và y = ∛x;
c) Đồ thị hai hàm số y = 2x2 và y = x4 – 2x2 trong miền x ≥ 0.
Lời giải:
a) Diện tích S cần tìm:
![]()
b) Hoành độ giao điểm của đồ thị hai hàm số y = √x và y = ∛x là nghiệm của phương trình:
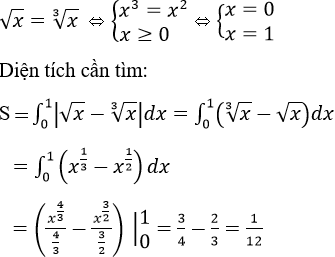
c) Phương trình hoành độ giao điểm đồ thị hai hàm số:
y = 2x2 và y = x4 – 2x2 (với x > 0)
2x2 = x4 – 2x2 ⇔ x4 – 4x2 = 0
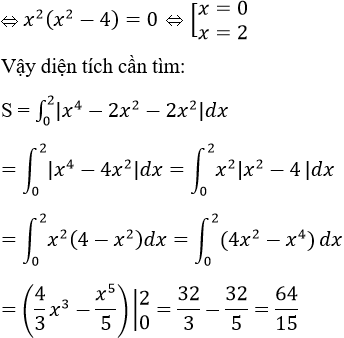
Bài 28 Trang 167 SGK
Tính diện tích các hình phẳng bởi giới hạn.
a) Đồ thị hàm số y = x2 – 4; y = -x2 – 2x và hai đường thẳng x = -3, x = -2.
b) Đồ thị hàm số y = x2 – 4 và y = -x2 – 2x
c) Đồ thị hàm số y = x3 – 4x, trục hoành, đường thẳng x = -2 và đường thẳng x = 4.
Lời giải:
a) Dựa vào hình vẽ ta thấy diện tích phẳng cần tìm là:
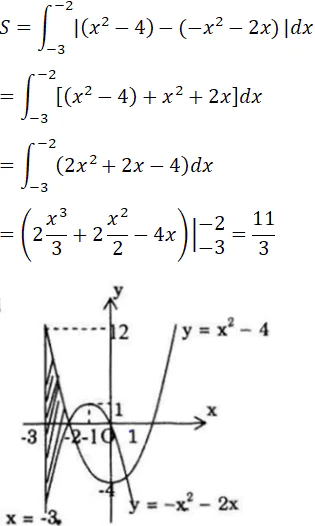
Chú ý: ở câu này, nếu không vẽ hình thì phải chứng tỏ rằng ∀x∈ (-3; -2) thì (x4 – 4) – (x2 – 2x) ≥0 để áp được giá trị tuyệt đối.
b) Phương trình hoành độ giao điểm đồ thị hai hàm số đã cho là:
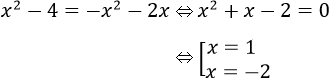
Dựa vào hình vẽ ở câu a ta có:
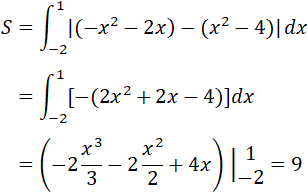
c) Diện tích cần tìm:
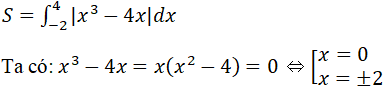
Ta có bảng xét dấu sau:
| x | -∞ | -2 | 0 | 2 | +∞ | ||||
| x | – | | | – | 0 | + | | | + | ||
| x2 – 4 | + | 0 | – | | | – | 0 | + | ||
| x(x2 – 4 ) | – | 0 | + | 0 | – | 0 | + |
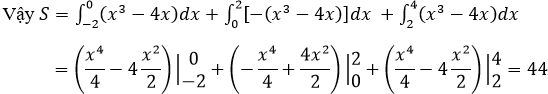

















Bình Luận
Để Lại Bình Luận Của Bạn