Bài 4. Đồ thị của hàm số và phép tịnh tiến hệ tọa độ | Bài giải GIẢI TÍCH 12 (Nâng Cao) | CHƯƠNG I - ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ - Lớp 12 - Sách Bài Giải

Bài 29 trang 27 SGK

Xác định đỉnh I của mỗi parabol (P) sau. Viết công thức chuyển hệ tọa độ trong phép tính tiến theo vectơ OI và viết Phương trình của Parabol (P) đối với hệ tọa độ IXY.

a) y = 2x² – 3x + 1

c) y = x – 4x²

d) y = 2x² – 5

Lời giải:

a) Đỉnh I có tọa độ I(3/4; -1/8)

Công thức chuyển tọa độ trong phép tính tiến theo vectơ OI là:

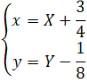
Phương trình của Parabol đối với hệ tọa độ IXY là:

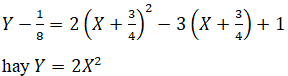
b) Đỉnh I(1; -7/2)

Công thức chuyển hệ tọa đọ trong phép tịnh tiến theo vectơ OI là:

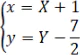
Phương trình của Parabol đối với hệ tọa độ IXY là:

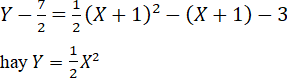
c) Đỉnh I(1/8; 1/16)

Công thức chuyển hệ trục tọa độ trong phép tịnh tiến theo vectơ OI là:

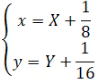
Phương trình của Parabol đối với hệ tọa độ IXY là:

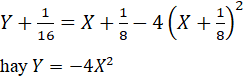
d) Đỉnh I(0; -5)

Công thức chuyển hệ trục tọa độ trong phép tịnh tiến theo vectơ OI là:

Phương trình của Parabol đối với hệ tọa độ IXY là:

Y – 5 = 2X² – 5 hay Y = 2X²

Bài 30 trang 27 SGK

Cho hàm số y = f(x) = x³ – 3x² + 1

a) Xác định điểm I thuộc đồ thị (C) của hàm số đã cho biết rằng hoành độ của điểm I là nghiệm của Phương trình f’’(x) = 0.

b) Viết công thức chuyển hệ tọa độ trong phép tịnh tiến vectơ OI và viết Phương trình của đường cong với hệ tọa độ IXY. Từ đó suy ra bằng I là tâm đối xứng đường cong (C).

c) Viết phương trình tiếp tuyến của đường cong (C) tại điểm I đối với hện tọa độ Oxy. Chứng minh rằng trên khoảng (-∞; 1) đường cong (C) nằm phía dưới tiếp tuyến tại I của (C) và trên khoảng (1; +∞) đường cong (C) nằm phía trên tiếp tuyến đó.

Lời giải:

a) f'(x)= 3x² – 6x

f''(x) = 6x – 6; f''(x) = 0 ⇔ x = 1 ⇒ f(1) = -1

Vậy I(1; -1)

b) Công thức chuyển hệ trục tọa độ trong phép tịnh tiến theo vectơ OI:

Phương trình của (C) đối với hệ trục IXY là:

y – 1 = (X + 1)³ – 3(X + 1)² + 1 hay Y = X³ – 3X

Vì hàm số Y = X³ – 3X là hàm số lẻ nên đồ thị của nó nhận gốc tọa độ I làm tâm đối xứng.

c) * Tiếp tuyến với (C) tại I(1; -1) đối với hệ tọa độ Oxy là:

y = f'(1)(x – 1)+f(1) với f’(1) = -3; f(1) = -1

Nên phương trình tiếp tuyến: y= -3(x – 1) + (-1) hay y = -3x + 2

Xét hiệu (x³ – 3x² + 1) – (-3x+2)= (x – 1)³

Với x ∈ (-∞; 1) ⇒ (x – 1)³< 0 ⇔ x³ – 3x² + 1 < -3x +2 nên đường cong (C): y = x³ – 3³ + 1 nằm phía dưới tiếp tuyến y = -3x + 2

Với x ∈ (1; +∞) ⇒ (x – 1)³ > 0 ⇔ x³ – 3x² + 1 > -3x + 2 nên đường cong (C): nằm phía trên tiếp tuyến tại I.

Bài 31 trang 27 SGK

Cho đường cong (C) có phương trình và điểm I(-2; 2). Viết công thức chuyển hệ tọa độ trong phép tịnh tiến vectơ OI và viết phương trình của đường cong (C) đối với hệ IXY. Từ đó suy ra I tâm đối xứng của (C).

Lời giải:

Công thức chuyển hệ tọa độ trong phép tịnh tiến theo OI:

Phương trình (C) trong hệ tọa độ IXY:

Vì Y = là hàm số lẻ nên (C) nhận gốc tọa độ I làm tâm đối xứng.

Bài 32 trang 28 SGK

Xác định tâm đối xứng của đồ thị mỗi hàm số sau đây.

Hướng dẫn. b) Viết công thức đã cho dưới dạng

Lời giải:

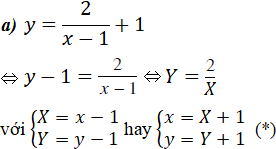
(*) là công thức chuyển hệ tọa độ trong phép tịnh tiến theo vectơ OI với I(1; 1) (đối với hệ trục Oxy)

Đối với hệ trục IXY, hàm số y = 2/X là hàm số lẻ nên đồ thị nhận gốc tọa độ làm tâm đối xứng.

Vậy tâm đối xứng của đồ thị hàm số là I(1; 1).

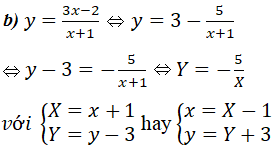
Đây là công thức chuyển hệ trục tọa độ trong phép tịnh tiến theo vectơ OI với I(-1; 3)

Vì Y = -5/X là hàm lẻ nên đồ thị nhận gốc tọa độ I làm tâm đối xứng.

Vậy tâm đối xứng của đồ thị hàm số: là I(-1; 3)

Bài 33 trang 28 SGK

Cho đường cong (C) có phương trình , trong đó a ≠ 0, c ≠ 0 và I(x_o, y_o) thõa mãn y_o = ax_o + b. Viết công thức chuyển hệ tọa độ trong phép tính tiến theo vectơ OI và phương trình của (C) đối với hệ tọa độ IXY. Từ đó suy ra rằng I là tâm đối xứng của đường cong (C).

Lời giải:

Công thức chuyển hệ tọa độ trong phép tịnh tiến theo OI với I(x_o, y_o) là:

Phương trình của (C) đối với hệ tọa độ IXY.

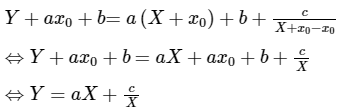
Do đó, hàm số là hàm số lẻ nên đồ thị (C) nhận gốc tọa độ tâm I làm tâm đối xứng.