Câu hỏi và bài tập ôn tập chương II | Bài giải GIẢI TÍCH 12 (Nâng Cao) | CHƯƠNG II - HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT - Lớp 12 - Sách Bài Giải

Bài 84 trang 130 SGK

So sánh p và q, biết:

Lời giải:

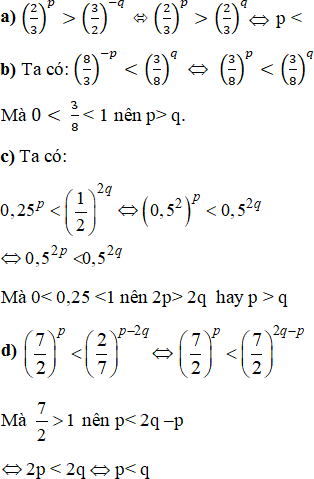
Bài 85 trang 130 SGK

Cho x < 0. Chứng minh rằng:

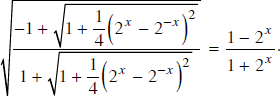
Lời giải:

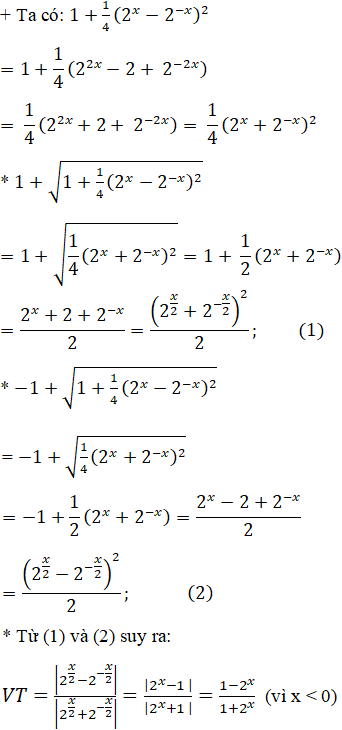
Bài 86 trang 130 SGK

Tính:

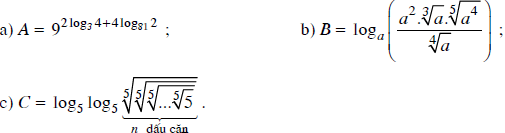
Lời giải:

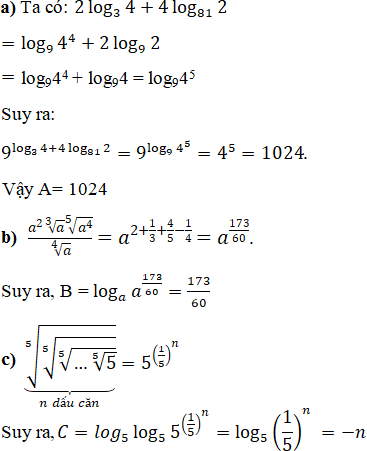
Bài 87 trang 130 SGK

Chứng minh rằng log₂⁡3 > log₃⁡4.

Lời giải:

Ta có: log₂⁡3>0; log₃⁡4>0. Bất Phương trình log₂3 > log₃4 tương dương với:

Mặt khác:

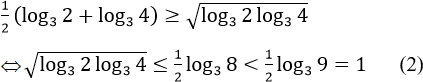
Từ (1) và (2) ⇒ điều phải chứng minh.

Bài 88 trang 130 SGK

Gọi c là cạnh huyền, a và b là hai cạnh vuông của một tam giác vuông. Chứng minh rằng

log_b+c⁡a+log_c–b⁡a = 2 log_b+c⁡a.log_c–b⁡a

Lời giải:

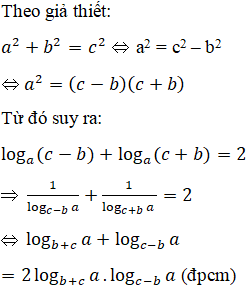
Bài 89 trang 131 SGK

Chứng minh rằng hàm số

thỏa mãn hệ thức xy' + 1 = e^y.

Lời giải:

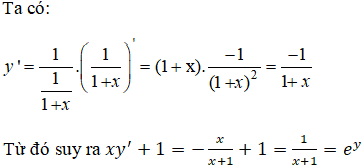
Bài 90 trang 131 SGK

Giả sử đồ thị (G) của hàm số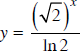

cắt trục tung tại điểm A và tiếp tuyến của (G) tại A cắt trục hoành tại điểm B. Tính giá trị gần đúng của diện tích của tam giác OAB (chính xác đến hàng phần nghìn).

Lời giải:

Cách 1. 

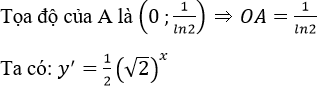
Suy ra hệ số góc của tiếp tuyến của đồ thị G tại A là:

Trong tam giác OAB, ta có:

Do đó diện tích tam giác OAB là

Cách 2.

Tiếp tuyến tại A có phương trình:

⇒ Tọa độ của B là nghiệm của hệ phương trình:

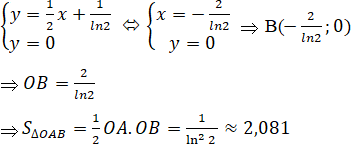
Bài 91 trang 131 SGK

Kí hiệu M là một điểm thuộc đồ thị của hàm số y = log_a⁡x. Trong hai khẳng định a > 1 và 0 < a < 1, khẳng định nào đúng trong mỗi trường hợp sau? Vì sao?

a) M có tọa độ (0,5; -7);

b) M có tọa độ (0,5; 7);

c) M có tọa độ (3; 5,2);

d) M có tọa độ (3; -5,2).

Lời giải:

Ta có các nhận xét sau:

* Áp dụng tính chất của hàm số logarit đồng biến trên (0; +∞) khi a > 1, nghịch biến trên (0; +∞) khi 0 < a < 1.

* Với mọi a > 0, a ≠ 1 đồ thị hàm số luôn đi qua điểm A(1; 0) tức là log_a1 = 0 (1)

a) Ta có log_a 0,5 = -7 (2)

Từ (1) và (2) ta có: 1 > 0,5 và 0 > -7

⇒ Hàm số đồng biến trên (0; +∞) nên a > 1.

b) Ta có; log_a0,5 = 7 (3)

Từ (1) và (3) ta có: 1 > 0,5 nhưng 0 < 7

⇒ Cơ số a thỏa mãn: 0 < a < 1.

c) Ta có log_a3 = 5,2 (4)

Từ (1) và ( 4) suy ra, 1 < 3 và 0 < 5,2

⇒ Cơ số a > 1.

d) Ta có: log_a3 = -5,2 (5)

Từ (1) và (5) ta có: 1 < 3 nhưng 0 < -5,2

⇒ Cơ số a thỏa mãn: 0 < a < 1.

Bài 92 trang 131 SGK

Các loài cây xanh trong quá trình quang hợp sẽ nhận được một lượng nhỏ cacbon 14 (một đồng vị của cacbon). Khi bộ phận của một cái cây nào đó bị chết thì hiện tượng quang hợp cũng ngưng và nó sẽ không nhận thêm cacbon 14 nữa. Lượng cacbon 14 của bộ phận đó sẽ phân hủy một cách chậm chạp, chuyển hóa thành nitrogen 14. Biết rằng nếu gọi P(t) là số phần trăm cacbon 14 còn lại trong một bộ phận của một cây xanh sinh trưởng từ t năm trước P(t) được tính theo công thức

Phân tích một mẫu gỗ từ một công trình kiến trúc cổ, người ta thấy lượng cacbon 14 còn lại trong mẫu gỗ đó là 65%. Hãy xác định niên đại của công trình kiến trúc đó.

Lời giải:

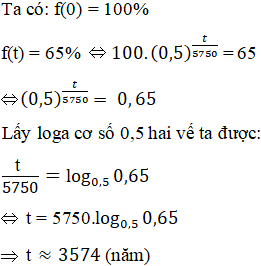
Bài 93 trang 131 SGK

Giải phương trình:

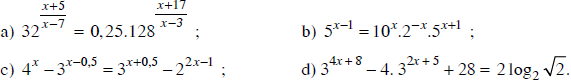
Lời giải:

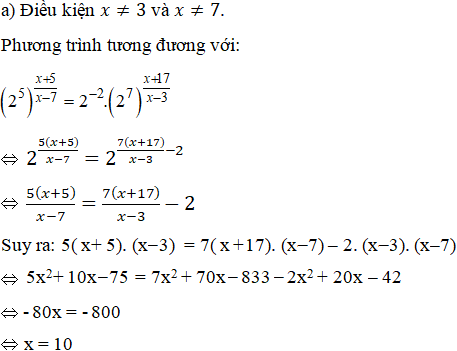
Vậy S = {10}.

Vậy S = {-2}.

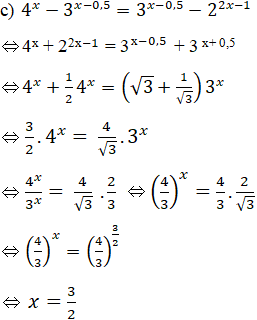
Vậy S = {3/2}.

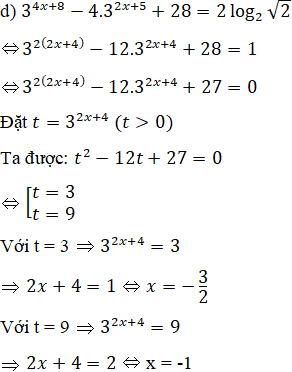
Vậy S = {-3/2; -1}.

Bài 94 trang 131 SGK

Giải các phương trình

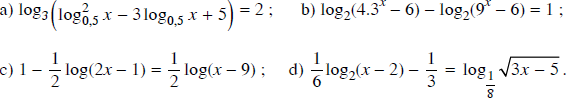
Lời giải:

a) log₃(log²_0,5x − 3log_0,5x + 5) = 2

Điều kiện: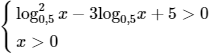

Ta có:

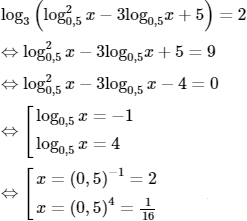
Vậy S = {2; 1/16}.

b) log₂(4.3^x − 6) − log_2⁡(9^x − 6) = 1

Điều kiện:

Ta có:

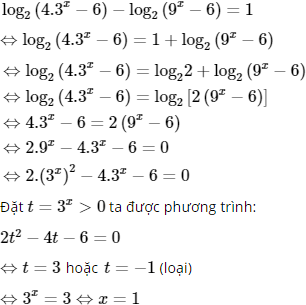
Vậy S = {1}.

c)

Điều kiện:

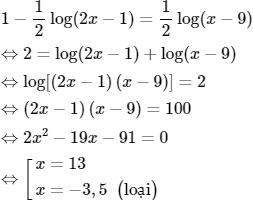
Vậy S = {13}.

d)

Điều kiện: x > 2.

Với điều kiện x > 2, ta chỉ nhận nghiệm x = 3.

Vậy S = {3}.

Bài 95 trang 132 SGK

Giải phương trình

4^x – 3^x = 1.

Lời giải:

Phương trình tương đương với

Dễ thấy x = 1 là nghiệm của phương trình, ta chứng minh x = 1 là nghiệm duy nhất của phương trình. Thật vậy:

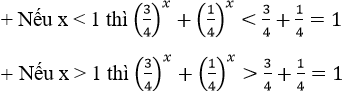
Vậy x = 1 là nghiệm của phương trình.

Bài 96 trang 132 SGK

Giải các hệ phương trình

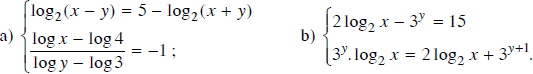
Lời giải:

a) Điều kiện: x – y > 0; x + y > 0; y ≠ 3.

Hệ phương trình tương đương với

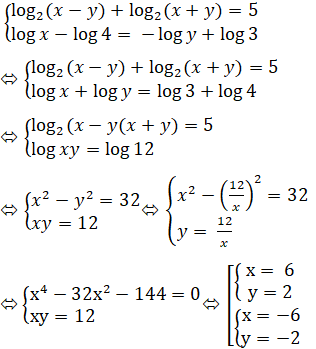
Kết hợp với điều kiện, vậy nghiệm của hệ phương trình là: (x; y) = (6; 2).

b) Đặt u = log_2⁡x; v = 3^x (v > 0) ta có hệ phương trình:

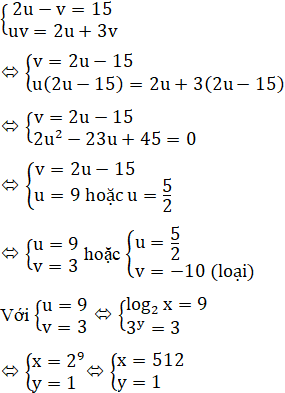
Vậy hệ phương trình có nghiệm (x, y) là (512; 1).

Bài 97 trang 132 SGK

Giải các bất phương trình sau

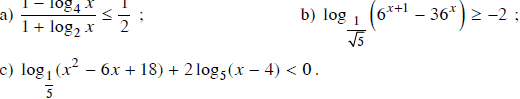
Lời giải: