Nội Dung Chính
Bài 37 trang 208 SGK
Với x, y nào thì số phức đó là số thực?
a) (2 − 3i)3 ;
![]()
c) (x + iy)2 − 2(x + iy) + 5 (x, y ∈ R). Với x,y nào thì số phức đó là số thực?
Lời giải:
a) Ta có: (2 − 3i)3
= 8 − 36i − 54 + 27i
= -46 − 9i
Vậy phần thực là -46 và phần ảo là -9.
b) Ta có:
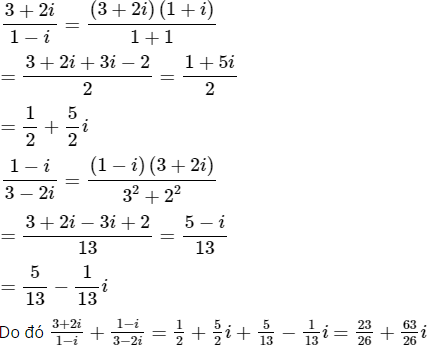
Vậy phần thực là 23/26 và phần ảo là 63/26.
c) Ta có: (x + iy)2 − 2(x + iy) + 5
= x2 − y2 + 2xyi − 2x− 2iy + 5
= (x2 − y2 − 2x + 5) + 2y(x − 1)i
Vậy phần thực là: x2 − y2 − 2x + 5, phần ảo là: 2y(x − 1).
Để z là số thực thì: 2y(x − 1) = 0 ⇔ y = 0 hoặc x = 1.
Bài 38 trang 209 SGK
Chứng minh rằng |z| = |w| = 1 thì số
![]()
là số thực (giả sử 1 + zw ≠ 0).
Lời giải:
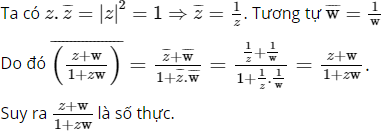
Cách khác:
Giả sử z = a + bi, w = a' + b'i với a2 + b2 = a'2 + b'2 = 1 và 1 + zw ≠ 0
Vì |z| = 1 nên ![]()
Khi đó, ta có:
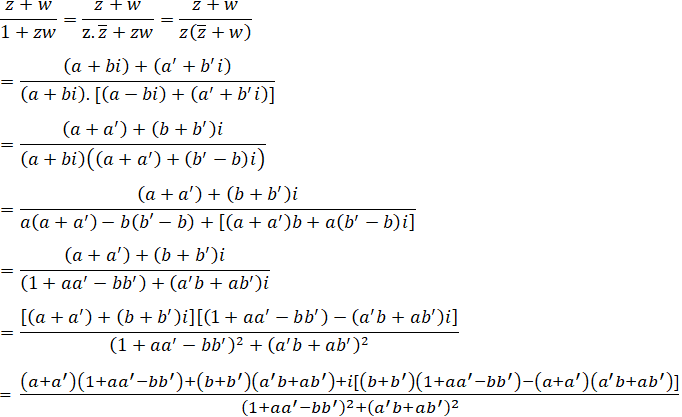
Xét phần ảo ở trên tử số ta có: (b + b')(1 + aa' − bb') − (a + a')(a'b + ab')
= b + baa' − b2b'+ b'+ b' aa' − bb'2 − aa' b − a2b' − a'2 b − a'ab'
= b + b'− b'(a2 + b2 ) − b(b'2 + a'2)
= b + b' − b' − b = 0
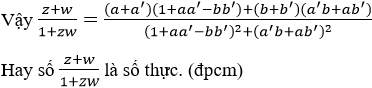
Bài 39 trang 209 SGK
Giải các phương trình sau trên C:
a) (z + 3 − i)2 − 6(z + 3 − i) + 13 = 0 ;
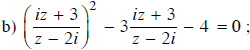
c) (z2 + 1)2 + (z + 3)2 = 0.
Lời giải:
a) (z + 3 − i)2 − 6(z + 3 − i) + 13 = 0
Đặt z + 3 − i = t, ta có phương trình: t2 − 6t + 13 = 0
Có δ' = -4 = (2i)2 ⇒ t1 = 3 + 2i; t2 = 3 − 2i
Với t1 = 3 + 2i ⇒ z + 3 − i = 3 + 2i ⇒ z = 3i
Với t2 = 3 − 2i ⇒ z + 3 − i = 3 − 2i ⇒ z = -i
Vậy phương trình có 2 nghiệm S = {3i; −i}.
b) ![]()
Ta có phương trình: t2 − 3t − 4 = 0
⇒ t1 = -1 hoặc t2 = 4
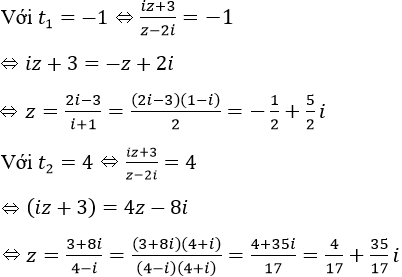
Vậy phương trình có hai nghiệm ![]()
c) (z2 + 1)2 + (z + 3)2 = 0
⇔ (z2 + 1)2 = -(z + 3)2
⇔ (z2 + 1)2 = [(z + 3)i]2
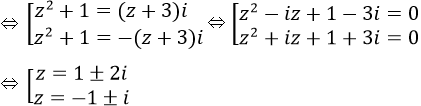
Vậy phương trình đã cho có 4 nghiệm S = {1−2i; −1+i; 1+2i; −1−i}.
Bài 40 trang 209 SGK
Xét các số phức:
![]()
a) Viết z1; z2; z3 dưới dạng lượng giác.
b) Từ câu a), hãy tính cos(7π/12) và sin(7π/12).
Lời giải:
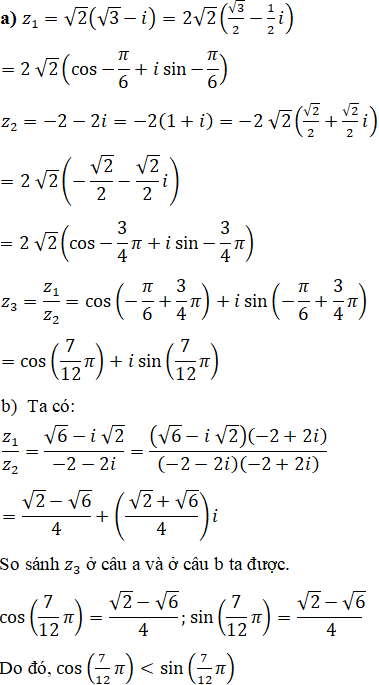
Bài 41 trang 209 SGK
Cho z = (√6 + √2) + i(√6 – √2).
a) Viết z2 dưới dạng đại số và dưới dạng lượng giác.
b) Từ câu a), hãy suy ra dạng lượng giác của z.
Lời giải:
a) Ta có: z2 = (√6 + √2)2 – (√6 – √2)2 + 2i(√6 + √2)(√6 – √2) = 8√3 + 8i
Mặt khác:
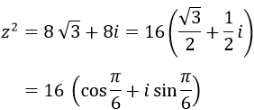
b) Ta có: z là một căn bậc hai của z2 nên ![]()
Bài 42 trang 209 SGK
a) Bằng cách biểu diễn hình học các số phức 2 + i; 3 + i, hãy chứng minh rằng nếu tana = 1/2, tanb = 1/3 với a, b ∈ (0; π/2) thì a + b = π/4.
b) Bằng cách biểu diễn hình học các số phức 2 + i, 5 + i, 8 + i, hãy chứng minh rằng nếu tana = 1/2, tanb = 1/5, tanb = 1/8 với a, b, c ∈ (0; π/2) thì a + b + c = π/4.
Lời giải:
a) Số z = 2 + i có một acgumen là a với tana = 1/2;
Số z’ = 3 + i có số acgumen là b với tanb = 1/3.
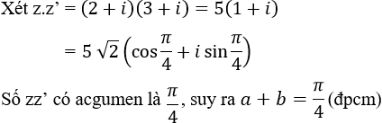
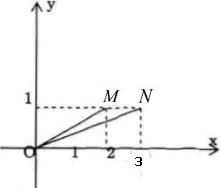
b) Số z1 = 2 + i có acgumen là a với tana = 1/2;
z2 = 5 + i có một acgumen là b với tanb = 1/5;
z3 = 8 + i có một acgumen là c với tanc = 1/8.
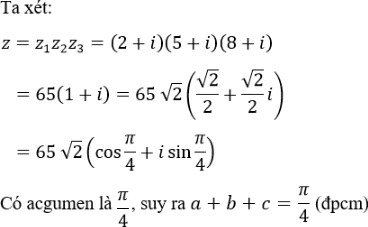

















Bình Luận
Để Lại Bình Luận Của Bạn