Nội Dung Chính
Câu hỏi và bài tập
Bài 1 trang 75 SGK
Trong các khẳng định sau, khẳng định nào đúng khẳng định nào sai?
a) Với số thực a và số nguyên m, n, ta có:
![]()
b) Với số thực a, b cùng khác 0 và số nguyên n, ta có:
![]()
c) Với số thực a, b thỏa mãn 0 < a < b với số nguyên a, ta có
an < bn.
d) Với số thực a ≠ 0 và hai số nguyên m, n, ta có
Nếu m > n thì am > an.
Lời giải:
a) Sai: Cần sửa lại thành: Với số thực a khác 0 và số nguyên m, n ta có:
![]()
b) Đúng.
c) Sai. Chẳng hạn: a0 = b0
d) Sai. Chẳng hạn (−1)3 < (−1)2
Bài 2 trang 75 SGK
Xét khẳng định: “Với số thực a và hai số hữu tỉ r, s, ta có (ar)s = ars. Với điều kiện nào trong các điều kiện sau thì khẳng định trên là đúng:
A. a bất kì B. a ≠ 0 C. a > 0 D. a < 0
Lời giải:
Vì r và s là hai số hữu tỉ nên để có: (ar)s = ar.s thì a > 0.
Chọn C.
Bài 3 trang 76 SGK
Viết các số sau dưới dạng số nguyên hay phân số tối giản:
![]()
Lời giải:
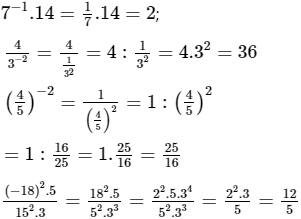
Bài 4 trang 76 SGK
Thực hiện phép tính
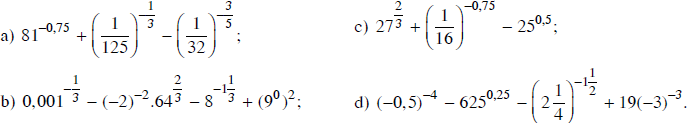
Lời giải:
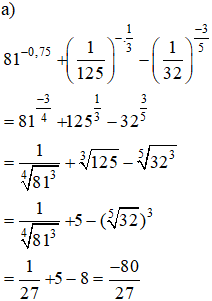
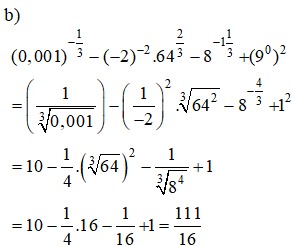
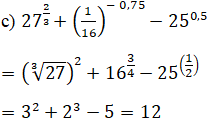
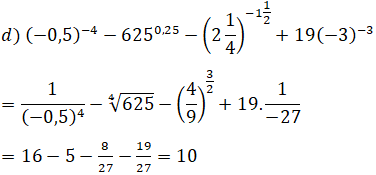
Bài 5 trang 76 SGK
Đơn giản biểu thức (với a, b là những số dương)
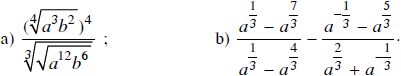
Lời giải:
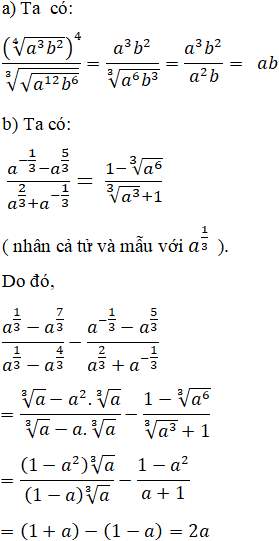
Bài 6 trang 76 SGK
So sánh các số:
![]()
Lời giải:
a)
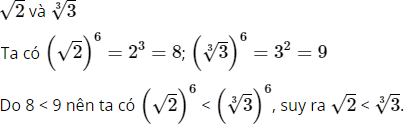
Cách khác:
Giả sử √2 < ∛3 ⇔ (√2)2 < 3 ⇔ 2 √2 < 3 ⇔ 8 < 9 đúng.
Vậy √2 < ∛3
b)
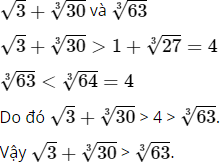
Cách khác:
Giả sử √3+∛30 < ∛63 ⇔ 3√3 + 9∛30 + 3√3∛(302) + 30 < 63
⇔ 3 √3 + 9∛3 + 3√3∛(302) < 33 (*)
Ta có 3√3 > 3
9∛30 > 9∛27= 27
3√3∛(302) > 3 ∛(27.27) = 27 ⇒ 3√3 + 9∛30 + 3√3∛(302) > 3 + 27 + 27 > 33
Vậy (*) sai ⇒ √3+∛30 > ∛63
c)
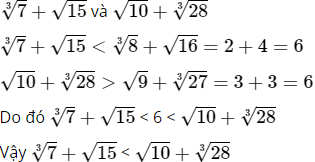
Cách khác:

Bài 7 trang 76 SGK
Chứng minh ![]()
Lời giải:
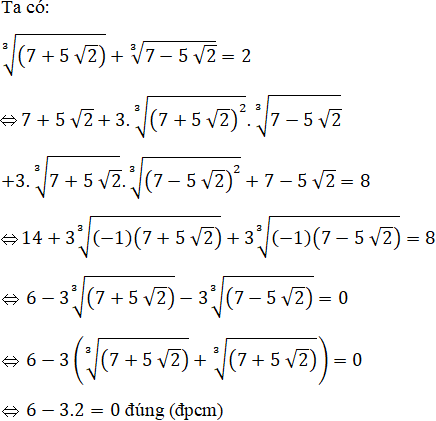
Luyện tập
Bài 8 trang 78 SGK
Đơn giản biểu thức
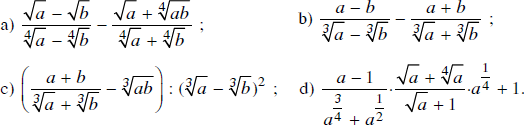
Lời giải:
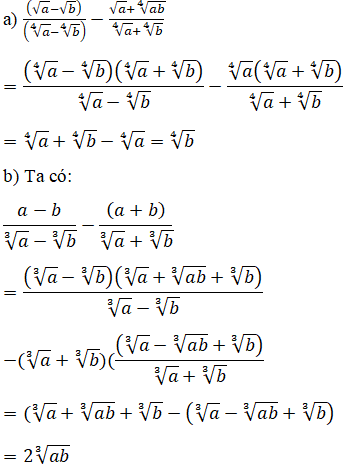
Bài 9 trang 78 SGK
Từ tính chất của lũy thừa với số mũ nguyên dương, chứng minh:
![]()
Lời giải:
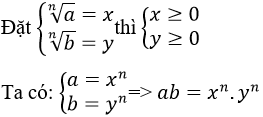
Áp dụng tính chất của lũy thừa với số mũ nguyên dương, ta có:
ab = (xy)n
![]()
Bài 10 trang 78 SGK
Chứng minh:
![]()
Lời giải:
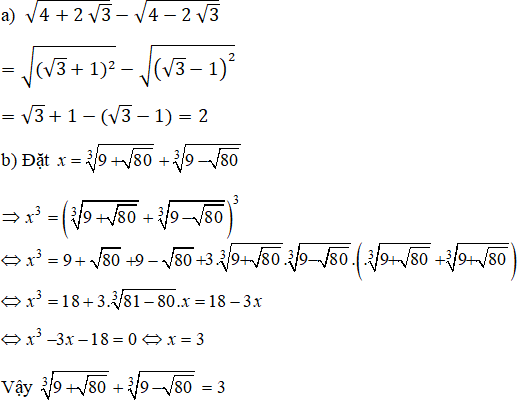
Bài 11 trang 78 SGK
So sánh các số
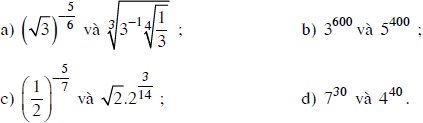
Lời giải:
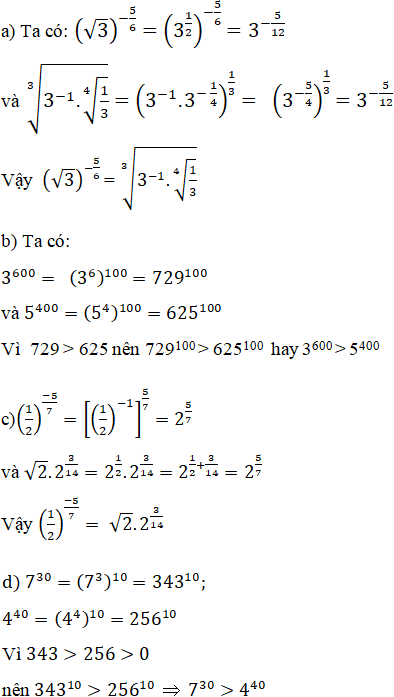
















Bình Luận
Để Lại Bình Luận Của Bạn