Bài 8. Hệ phương trình mũ và lôgarit | Bài giải GIẢI TÍCH 12 (Nâng Cao) | CHƯƠNG II - HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT - Lớp 12 - Sách Bài Giải

Câu hỏi và bài tập

Giải các hệ phương trình (bài 72 và bài 73):

Bài 72 trang 127 SGK

Giải các hệ phương trình:

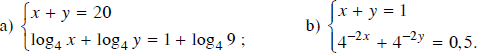
Lời giải:

Điều kiện: x > 0; y > 0

Hệ phương trình tương dương:

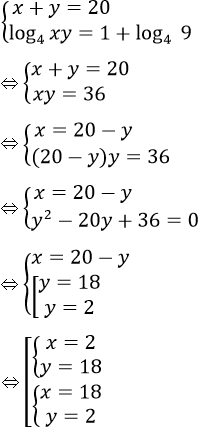
Vậy tập nghiệm của hệ phương trình là S = {(2; 18), (18; 2)}

Cách 1. Rút y = 1 – x từ phương trình đầu, thế vào phương trình thứ hai được:

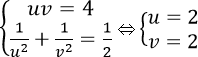
Đặt t = 4^2x (t > 0), ta được t² – 8t + 16 = 0 ⇔ t = 4

Với t = 4 ⇒ 4^2x = 4 ⇔ 2x = 1 ⇔ x = 1/2 ⇒ y = 1/2

Nghiệm của hệ là: S = {(1/2; 1/2)}.

Cách 2. x + y = 1 ⇔ 4x + y = 4 ⇔ 4x.4y = 4

Đặt u = 4x, v = 4y ta được:

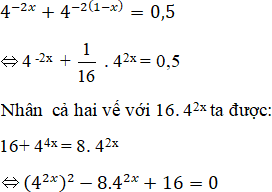
Vì u > 0; v > 0

⇒ Tập nghiệm của hệ phương trình là S = {(1/2; 1/2)}.

Bài 73 trang 127 SGK

Giải hệ phương trình:

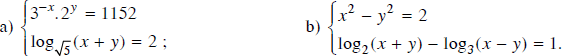
Lời giải:

a) Điều kiện: x + y > 0.

Từ phương trình thứ hai suy ra: x + y = (√5)² = 5 ⇒ y = 5 − x thay vào phương trình thứ nhất ta được:

3^−x.2^5−x = 1152

⇔ 3^−x.2^−x.2⁵ = 1152

⇔ 6^−x.32 = 1152

⇔ 6^−x = 36

⇔ x = −2

Với x = −2, ta có y = 5 –(−2) =7. 

Vậy S = {(−2; 7)}.

b) Điều kiện

Khi đó,

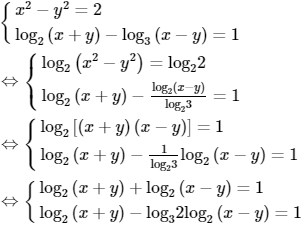
Đặt u = log₂(x + y) và v = log₂(x − y) ta được hệ:

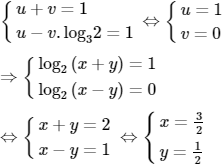
Vậy S = {(3/2; 1/2)}.

Luyện tập

Giải các phương trình (từ bài 74 và bài 78):

Bài 74 trang 127 SGK

a) log₂(3 – x) + log₂(1 – x) = 3

b) log₂(9 – 2^x) = 10log⁡^{(3 – x)}

c) 7^logx – 5^{logx + 1} = 3.5^{logx – 1} – 13.7^{logx – 1}

d) 6^x + 6^{x + 1} = 2^x + 2^{x + 1} + 2^{x + 2}

Lời giải:

a) log₂(3 – x) + log₂(1 – x) = 3

Điều kiện: x < 1.

Phương trình đã cho tương đương với

log₂[(3 – x).( 1 – x)] = 3

⇔ x = -1 hoặc x = 5 (loại)

Vậy S = {-1}.

b) log₂(9 – 2^x) = 10log⁡^{(3 – x)}

Điều kiện: x < 3.

Phương trình đã cho tương đương với

9 – 2^x = 2^{3 – x}

⇔ -(2^x)² + 9.2^x = 8 ( nhân cả 2 vế với 2x)

Vậy S = {0}.

c) 7^logx – 5^{logx + 1} = 3.5^{logx – 1} – 13.7^{logx – 1}

Điều kiện: x > 0

Khi đó, phương trình đã cho tương đương với phương trình:

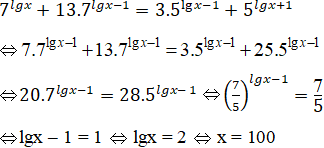
Vậy S = {100}.

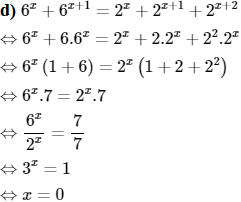
Vậy S = {0}.

Bài 75 trang 127 SGK

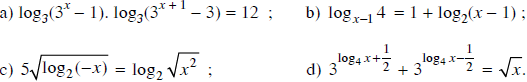
Lời giải:

a) Điều kiện:

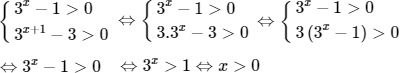
Ta có:

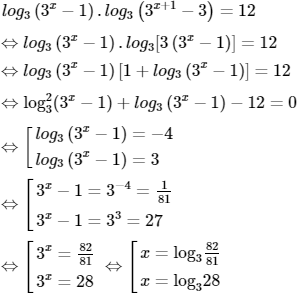
Vậy S = {log₃28; log₃(82/81)}.

b) Điều kiện: 0 < x – 1 ≠ 1 ⇔ 1 < x ≠ 2

Vậy S = {3; 5/4}.

c) Điều kiện: 

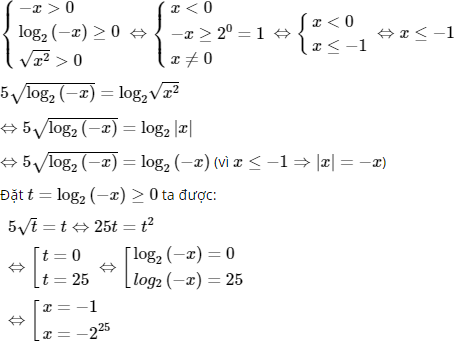
Vậy S = {−1; −2²⁵}.

d) Điều kiện: x > 0

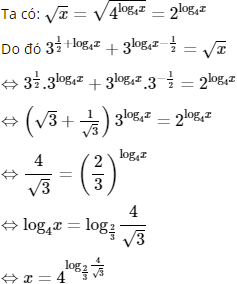
Bài 76 trang 127 SGK

Lời giải:

a) Điều kiện x ≠ 0.

Ta được phương trình:

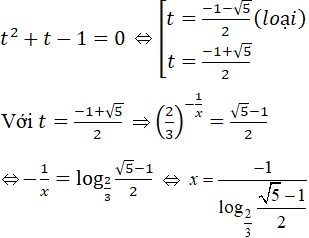
b) Điều kiện x > 0.

Phương trình đã cho tương đương với:

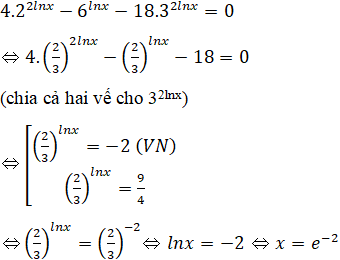
c) Điều kiện log2⁡x ≥ 0 ⇔ x ≥ 1.

Phương trình tương dương với:

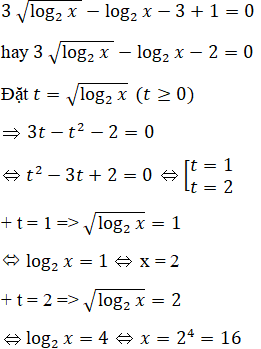
Vậy nghiệm của phương trình đã cho là: x= 2 và x= 16.

d) Điều kiện x > 0, ta có:

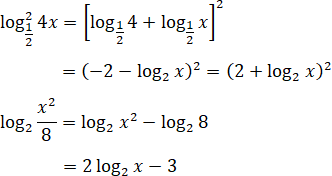
Phương tình đã cho tương đương với phương trình:

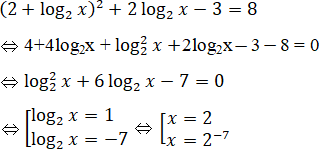
Bài 77 trang 127 SGK

Lời giải:

 

 

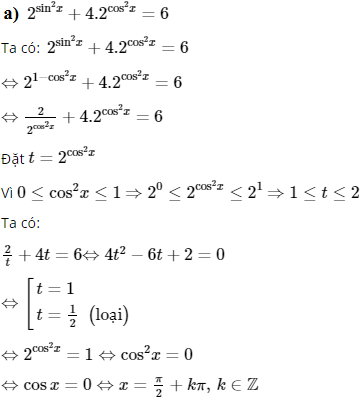
b) Ta có: 4^{3 + 2cos2x} – 7.4^{1 + cos2x} = 4^(1/2)

⇔ 4.4^{2(1 + cos2x)} – 7.4^{1 + cos2x} = 2

Đặt t = 4^{1 + cos2x} (t > 0).

Ta được phương trình:

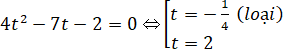
Với t = 2

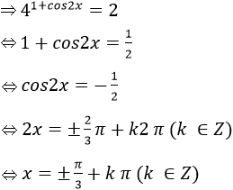
Bài 78 trang 127 SGK

Giải phương trình:

Lời giải:

a) Dễ thấy x = -1 là nghiệm.

Ta chứng minh x = -1 là nghiệm duy nhất.

Thật vậy:

VP = x + 4 < -1 + 4 = 3 ⇒ VT > VP

Phương trình không thỏa mãn với x < -1

VP = x + 4 > -1 + 4 = 3 ⇒ VT < VP

Phương trình vô nghiệm với x > -1

Vậy Phương trình có nghiệm duy nhất x = -1.

b) Dễ thấy: x = 2 là nghiệm của phương trình.

Ta chứng minh x = 2 là nghiệm duy nhất.

Thật vậy:

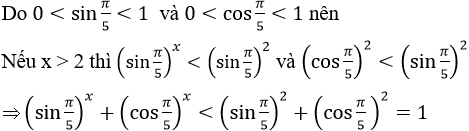
Tương tự:

Vậy phương trình có nghiệm duy nhất là x = 2.

Bài 79 trang 127 SGK

Giải hệ phương trình:

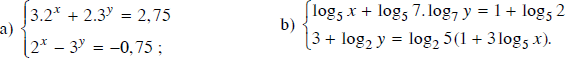
Lời giải:

Vậy S = {(−2; 0)}.

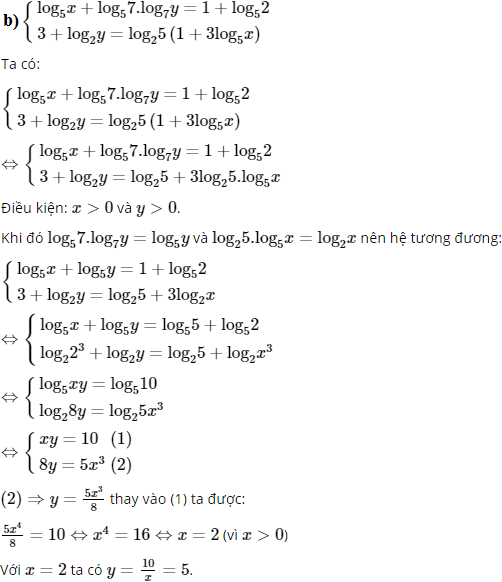
Vậy S = {(2; 5)}.