Nội Dung Chính
Bài 42 trang 97 SGK
Tìm sai lầm trong lập luận sau:
Ta có lne2 = 2lne = 2.1 = 2 và ln(2e) = lne + lne = 1 + 1 = 2. Từ đó suy ra e2 = 2e mà e ≠ 0 nên e = 2!
Lời giải:
Lập luận trên sai lầm chỗ ln(2e) = lne + lne.
Lập luận đúng là: ln(2e) = ln2 + lne.
Bài 43 trang 97 SGK
Biểu diễn các số sau đây theo a = ln2, b = ln5:
![]()
Lời giải:
+ ln500 = ln(53.22) = ln53 + ln22 = 3ln5 + 2ln2 = 3b + 2a
+ ln(16/25) = ln16 – ln25 = ln24 – ln(52) = 4ln2 – 2ln5 = 4a – 2b
+ ln6,25 = ln(625/100) = ln625 – ln100 = ln(54) – ln(52.22) = 4ln5 – 2ln5 – 2ln2 = 2ln5 – 2ln2 = 2b – 2a
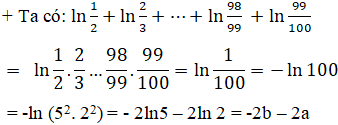
Bài 44 trang 97 SGK
Chứng minh:
![]()
Lời giải:
Ta biến đổi vế trái:
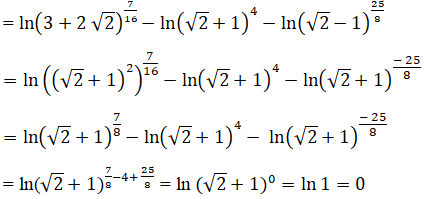
Bài 45 trang 97 SGK
Sự tăng trưởng của một loại vi khuẩn theo công thức S = A.ert, trong đó A là số lượng vi khuẩn ban đầu, r là tỉ lệ tăng trưởng (r > 0), t là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Hỏi sau 10 giờ có bao nhiêu của vi khuẩn? Sau bao lâu số lượng vi khuẩn ban đầu sẽ tăng gấp đôi?
Lời giải:
Sau 5 giờ, từ công thức S = A.ert ta có 300 = 100.e5r ⇒ 3 = e5r
![]()
Sau 10 giờ số lượng vi khuẩn là
![]()
⇒ S = 100.e2ln3 = 100.(eln3 )2= 100.32 = 100.9 = 900 (con)
Để số lượng vi khuẩn tăng lên gấp đôi thì:
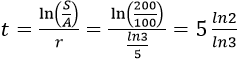
⇒ t ≈ 3,15 h = 3 giờ 9 phút.
Bài 46 trang 97 SGK
Cho biết chu kì bán hủy của chất phóng xạ Plutanium Pu239 là 24360 năm (tức là một lượng Pu239 sau 24360 năm phân hủy chỉ còn lại một nửa). Sự phân hủy được tính theo công thức S = Aert, trong đó, A là lượng chất phóng xạ ban đầu, r là tỉ lệ phân hủy hàng năm (r < 0), t là thời gian phân hủy, S là lượng còn lại phân hủy sau thời gian phân hủy t. Hỏi sau 10 gam Pu239 sau bao nhiêu năm sẽ phân hủy còn lại 1 gam?
Lời giải:
Tính tỉ lệ phân hủy hàng năm:
Ta có:
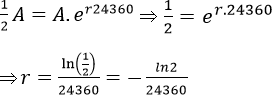
Gọi t0 là thời gian mà 10gam Pi239 phân hủy còn 1 gam ta có:
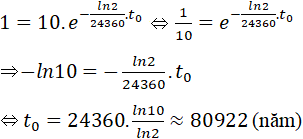

















Bình Luận
Để Lại Bình Luận Của Bạn