Bài tập trắc nghiệm khách quan chương IV | Bài giải GIẢI TÍCH 12 (Nâng Cao) | CHƯƠNG IV - SỐ PHỨC - Lớp 12 - Sách Bài Giải

Trong mỗi bài tập dưới đây, hãy chọn một phương án trong các phương án đã cho để được khẳng định đúng.

Bài 43 trang 210 SGK

Phần thực của z = 2i là

(A) 2;                           (B) 2i;

(C) 0;                           (D) 1.

Lời giải:

Ta có  z = 0 + 2i có phần thực là 0.

Chọn (C).

Bài 44 trang 210 SGK

Phần ảo của z = −2i là:

(A) - 2;                        (B) - 2i;

(C) 0;                           (D) - 1.

Lời giải:

Ta có z = −2i = 0 − 2i có phần ảo là −2.

Chọn (A).

Bài 45 trang 210 SGK

Số

(A) số thực;                             (B) số ảo;

(C) 0;                                       (D) 2.

Lời giải:

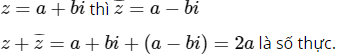
Chọn (A).

Bài 46 trang 210 SGK

Số là

(A) số thực;                             (B) số ảo;

(C) 0;                                       (D) 2i.

Lời giải:

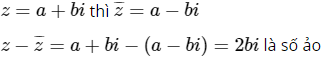
Chọn (B).

Bài 47 trang 210 SGK

Số 1/(1+i) bằng

(A) 1+i;                                     (B) 1/2(1−i);  

(C) 1–i;                                      (D) i.

Lời giải:

Chọn (B).

Bài 48 trang 210 SGK

Tập hợp các nghiệm của phương trình z = z/(z+i) là:

(A) {0; 1 − i};                  (B) {0};

(C) {1 − i};                      (D) {0; 1}.

Lời giải:

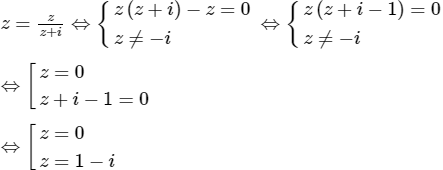
Chọn (A).

Bài 49 trang 210 SGK

Modun của 1 – 2i bằng

(A) 3;                           (B) √5;

(C) 2;                           (D) 1.

Lời giải:

z =1−2i thì |z| =√[1² + (−2)²] = √5

Chọn (B).

Bài 50 trang 210 SGK

Modun của −2iz bằng

(A) −2|z|;                       (B) √2z;

(C) 2|z|;                          (D) 2.

Lời giải:

|−2iz| = |−2i|.|z| = 2|z|

Chọn (C).

Bài 51 trang 210 SGK

Acgumen của −1 + i bằng

(A) 3π/4 + k2π (k ∈ Z);

(B) −π/4 + k2π (k ∈ Z);

(C) π/4 + k2π (k ∈ Z);

(D) π/2 + k2π ( k ∈ Z).

Lời giải:

Acgumen của −1 + i bằng 3π/4 + k2π (k ∈ Z)

Chọn (A).

Bài 52 trang 210 SGK

Nếu acgumen của z bằng −π/2 + k2π thì

(A) Phần ảo của z là số dương và phần thực của z bằng 0;

(B) Phần ảo của z là số âm và phần thực của z bằng 0;

(C) Phần thực của z là số âm và phần ảo của z bằng 0;

(D) Phần thực và phần ảo của z đều là số âm.

Lời giải:

Do đó phần thực bằng 0, phần ảo âm.

Chọn (B).

Bài 53 trang 211 SGK

Nếu z = cosφ − isinφ thì acgumen của z bằng:

(A) φ + k2π (k ∈ Z);

(B) −φ + k2π (k ∈ Z);

(C) φ + π + k2π (k ∈ Z);

(D) φ + π2 + k2π (k ∈ Z).

Lời giải:

z = cosφ − isinφ = cos(−φ) + isin(−φ)

Vậy z có argumen bằng −φ + k2π (k ∈ Z)

Chọn (B).

Bài 54 trang 211 SGK

Nếu z = −sinφ − icosφ thì acgumen của z bằng:

(A) −π/2 + φ + k2π (k ∈ Z);

(B) −π/2 − φ + k2π (k ∈ Z);

(C) π/2 + φ + k2π (k ∈ Z);

(D) π − φ + k2π (k ∈ Z).

Lời giải:

Ta có:

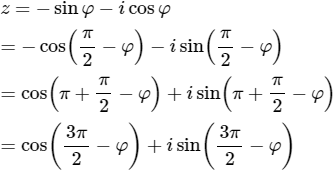
Argumen của z bằng 3π/2− φ + k2π = −π/2 − φ + (k + 1)2π = −π/2 − φ + 2lπ, l ∈ Z

Chọn (B).