Bài 9. Bất phương trình mũ và lôgarit | Bài giải GIẢI TÍCH 12 (Nâng Cao) | CHƯƠNG II - HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT - Lớp 12 - Sách Bài Giải

Giải các bất phương trình sau:

Bài 80 trang 129 SGK

a) 2^{3 – 6x} > 1                                                                                             b) 16^x > 0,125

Lời giải:

a) 2^{3 – 6x} > 1 ⇔ 2³ > 2^6x ⇔ 3 > 6x ⇔ x < 1/2

b) 16^x > 0,125 ⇔ 24^x > 2^-3 ⇔ 4x > -3 ⇔ x > -3/4

Bài 81 trang 129 SGK

a) log₅(3x – 1) < 1

c) log_0,5(x² – 5x+ 6) ≥ -1

Lời giải:

a) log₅(3x – 1) < 1

Điều kiện: x > 1/3

Bất phương trình tương đương:

log₅(3x – 1) < log₅5

⇔ 3x – 1< 5

⇔ x < 2

Kết hợp với điều kiện, ta được 1/3 < x < 2.

Vậy S = (1/3; 2).

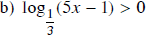
Điều kiện: 5x – 1 > 0 ⇔ x > 1/5

Bất phương trình tương đương: 5x – 1 < 1 ⇔ x < 2/5

Kết hợp với điều kiện ta được: 1/5 < x < 2/5.

Vậy S = (1/5; 2/5).

c) log_0,5(x² – 5x+ 6) ≥ -1

Điều kiện: x² – 5x+ 6 > 0

Bất phương trình tương đương: x² – 5x+ 6 ≤ (0,5)^-1

⇔ x² – 5x+ 6 ≤ 2

⇔ x² – 5x + 4 ≤ 0

⇔  1 ≤ x ≤ 4

Kết hợp với điều kiện, ta được tập nghiệm S = [1; 2) ∪ (3; 4].

Cách khác: x² – 5x+ 6 ≤ (0,5)^-1

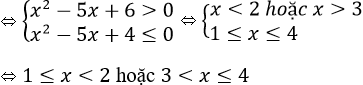
Vậy tập nghiệm S = [1; 2) ∪ (3; 4].

Bất phương trình tương đương:

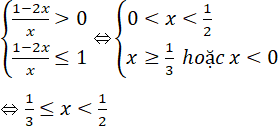
Vây tập nghiệm của bất phương trình là S = [1/3; 1/2).

Bài 82 trang 130 SGK

a) log²_0,5x + log_0,5x – 2 ≤ 0;                                                           b) 2^x + 2^{-x + 1} – 3 < 0.

Lời giải:

a) log²_0,5x + log_0,5x – 2 ≤ 0

Điều kiện: x > 0

Đặt t = log_0,5x, ta được: t² + t – 2 ≤ 0

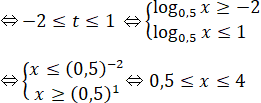
Kết hợp điều kiện, ta được: 0,5 ≤ x ≤ 4.

Vậy S = [0,5; 4].

b) 2^x + 2^{-x + 1} – 3 < 0

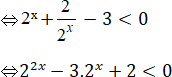
Đặt t = 2^x (t > 0), ta được: t² – 3t + 2 < 0 ⇔ 1 < t < 2

⇒ 1< 2x < 2 ⇔ 0 < x < 1

Vậy tập nghiệm của phương trình S = (0; 1).

Bài 83 trang 130 SGK

a) log_0,1(x² + x  – 2) > log_0,1(x + 3);                                                      b) log_1/3(x² – 6x + 5) + 2 log₃(2 – x) ≥ 0.

Lời giải:

a) log_0,1(x² + x  – 2) > log_0,1(x + 3)

Bất phương trình đã cho tương đương:

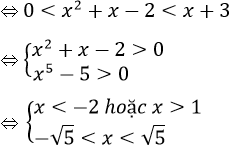
Vậy tập nghiệm của bất phương trình là S = (-√5; -2) ∪ (1; √5).

b) log_1/3(x² – 6x + 5) + 2 log₃(2 – x) ≥ 0

Khi đó,

log_1/3(x² – 6x + 5) + 2 log₃(2 – x) ≥ 0

⇔ log_1/3(x² – 6x + 5) ≥ log_1/3(2 – x)²

⇔ x² – 6x + 5 ≤ (2 – x)²

⇔ 2x – 1 ≥ 0

Bất phương trình tương đương với:

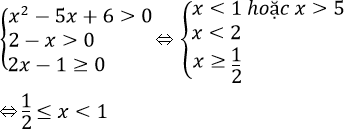
Vậy tập nghiệm của bất phương trình là: S = [1/2; 1).